SVM 支持向量机

Posted 2022-11-23 Debroon

SVM 支持向量机

• • SVM 原理
  • 最优化问题
  • 线性不可分
  • sklearn 调用 SVM
  • 核函数

 

---

SVM 原理

前置知识：用迭代策略来划分样本，请猛击《神经元的计算》。

SVM 也是用一条迭代的直线来划分不同数据之间的边界：

.- 是一条直线（线性函数）

• 能将苹果和橘子分为两个部分（具有分类功能，是一种二值分类）

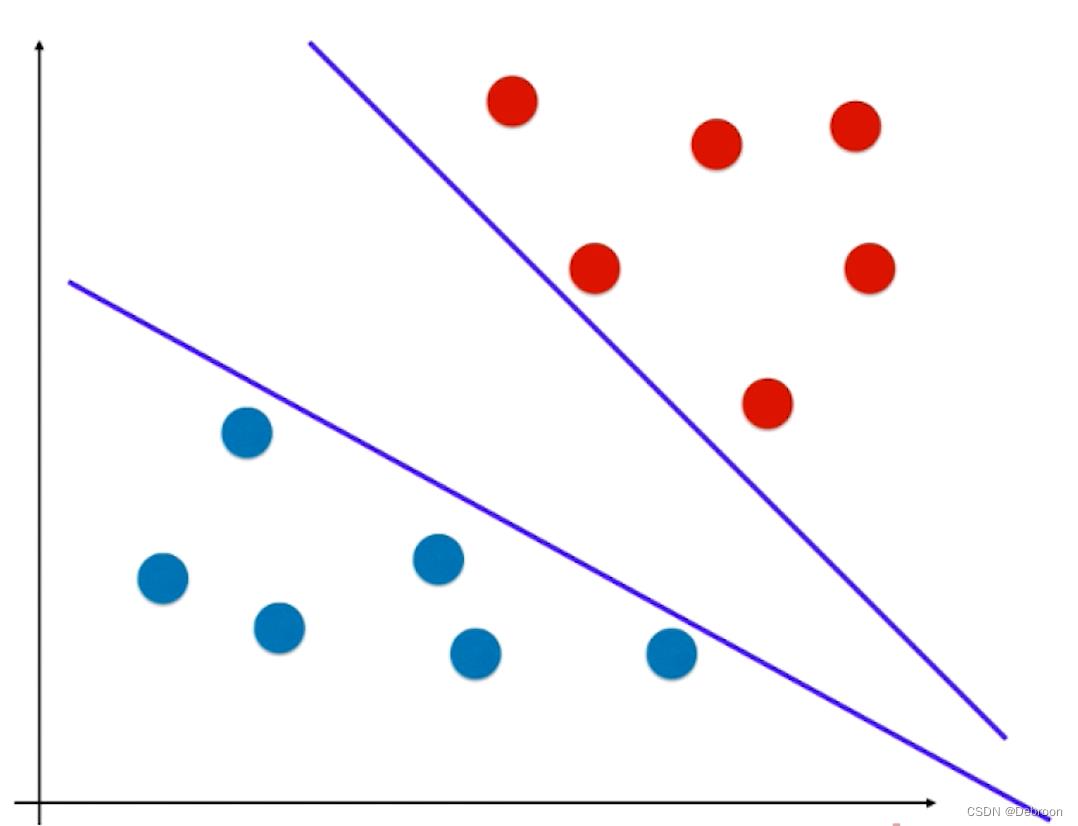
这样的线性函数，极端情况（直线逼近某一样本时），会把添加在附近的新样本误分在另外一侧，比如下图所示：

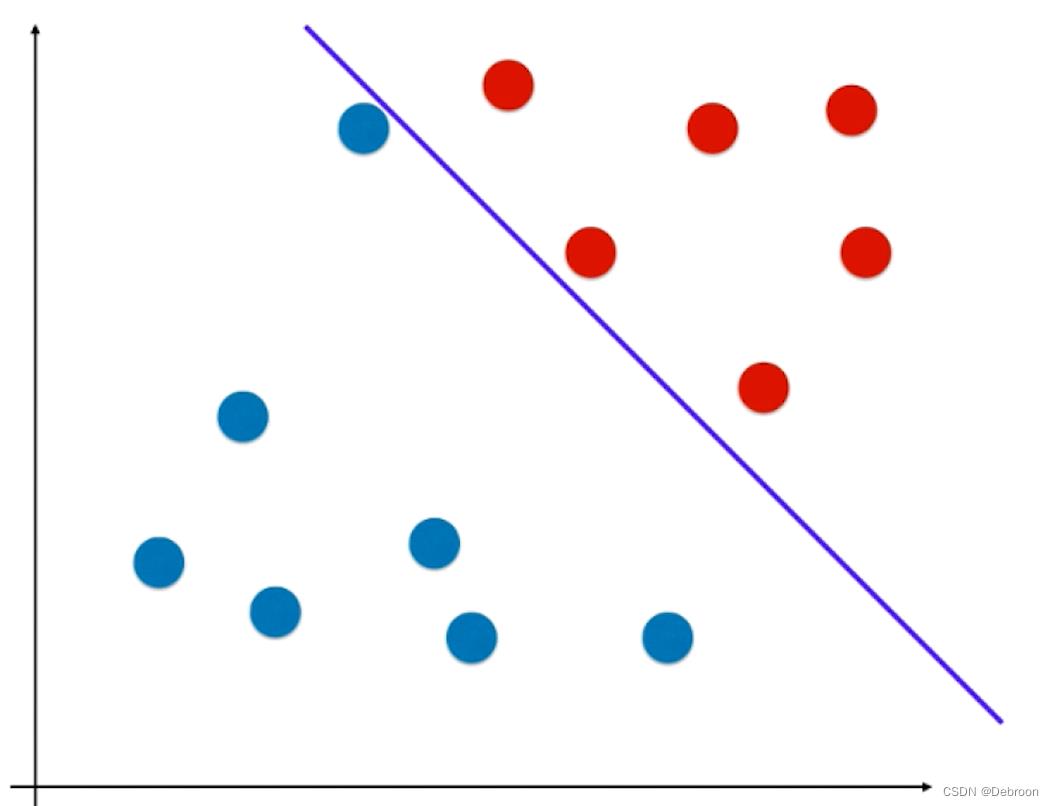
新添加的元素，按照距离来看，本应是属于红色样本。

结果因为直线过于逼近红色区域，导致被划分成蓝色样本了。

这个直线泛化能力不够好的问题，要么是在数据预处理部分做处理，要么是做正则化。

• 正则化的本质是一个概念，不同算法中的使用方式可能不同，但它们的目的都是一样的，都是在机器学习算法层面增加模型的泛化能力。

SVM 是在算法里面解决泛化问题，不同于线性函数的地方在于：

• 这条直线，一定位于苹果和橘子的正中间，尽可能的离俩个样本最远，如同男女课桌的军事分解线，处于正中间，不偏向任何一方（注重公平原则，才能保证双方利益最大化）。

SVM 尝试寻找一条最优的决策边界，距离俩个类别最近的样本最远。

• 俩个类别最近的样本（被直线划中的蓝点、红点），叫支持向量，就是支持向量机 SVM 取名的由来

我们会用一个 margin 来描述这个距离：

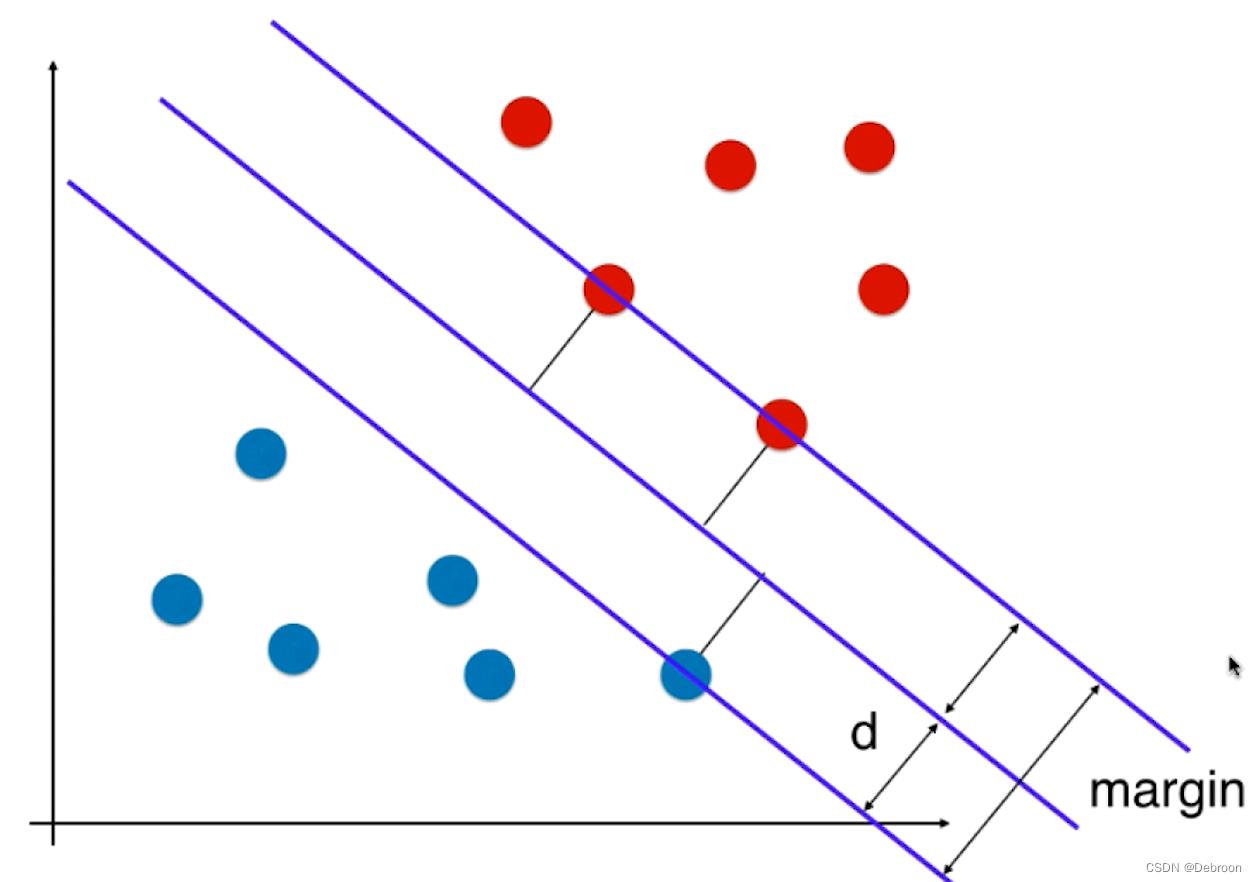
公平，就是要让 margin 最大化。

• 这种思维，也被称为 Hard Margin SVM，解决线性可分问题，找到一个决策边界，没有错误的将所有决策点进行划分。

• 但真实情况下，很多数据是线性不可分的，我们需要改进了 Hard Margin SVM，实现 Soft Margin SVM 解决线性不可分。

• 参数学习算法的固定套路：我们把算法思想（支持向量机的思想）转化为最优化问题、最优化目标函数。

 

---

最优化问题

因为 margin = 2d，margin 最大化也就是最大化 d。

还记得高中数学吗，点 (x, y) 到直线的距离公式：

• 点：$(x,y)$
• 直线方程：$Ax+By+C=0$
• 点 (x, y) 到直线 $Ax+By+C=0$ 的距离公式：$\frac{|Ax+By+C|}{\sqrt{A^2+B^2}}$

这只是基于二维平面情况，我们再把这个公式，拓展到 N 维。

N 维点到直线的距离（推导过程不清楚可搜索一下）：

• 点：$[x_1,x_2,x_3,\cdot \cdot \cdot ,x^n{]}^T=X$，这里的点就是支持向量
• 直线方程：$W^{T}X+b=0，W^T=[w_1,w_2,w_3,\cdot \cdot \cdot ,w_n]$
• 点到直线的距离公式：$\frac{|W^{T}x+b|}{||w||}，||w||=\sqrt{w_1^2+w_2^2+w_3^2+\cdot \cdot \cdot +w_n^2}$

分子 $|Ax+By+C|$ 就是 $|W^{T}x+b|$，分母 $\sqrt{(}{A}^2+B^2)$ 就是 $||w||$。

把这个公式代入 SVM 中：

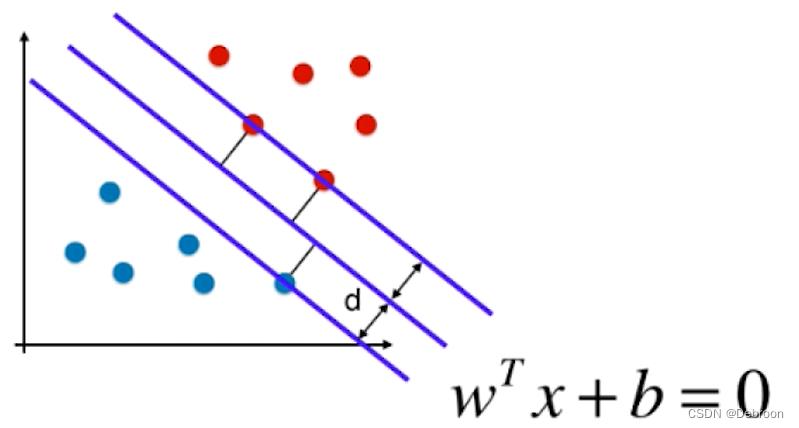
假设中间的直线方程是：$W^{T}x+b=0$

那上下俩条直线就可以这样表示了：

• 上：$\frac{W^T{x}^i+b}{||w||}>=d，y^i=1$
• 下：$\frac{W^T{x}^i+b}{||w||}<=-d，y^i=-1$

格式俩边都除以 d：

• 上：$\frac{W^T{x}^i+b}{||w||d}>=1，y^i=1$
• 下：$\frac{W^T{x}^i+b}{||w||d}<=-1，y^i=-1$

因为 $w、d$ 都是一个具体的数，我们可以约分。

分子、分母都除以 $||w||d$：

• 上：$W_d^T{x}^i+b_d>=1，y^i=1$
• 下： W d T x i + b d < = − 1 ， y i = − 1 W^T_dx^i+b_d<=-1，y^i=-1 Hard-Margin SVM（支持向量机）

  支持向量机(SVM)-- 最优间隔分类器（optimal margin classifier）

  支持向量机（support vector machine, SVM）

  数学建模学习（65）：零基础学会使用SVM支持向量机分类

  菜菜的sklearn课堂笔记支持向量机-线性SVM决策过程的可视化

  透过现象看本质，图解支持向量机