import java.util.List;

public interface BinNode 
	public Object getElement(); // 返回结点元素
	public void setElement(Object ob); // 设置结点元素
	public BinNode getLeft(); // 返回左孩子
	public void setLeft(BinNode leftnode);// 设置左孩子
	public BinNode getRight(); // 返回右孩子
	public void setRight(BinNode rightnode); // 设置右孩子
	public boolean isLeaf(); // 判断是否叶子结点
	
//	public void preordertraversal(BinNode root);// 先序遍历
//	public void preordertraversalwithStack(BinNode root);//栈实现非递归先序遍历
//	public void inordertraversal(BinNode node);// 中序遍历
//	public void inordertraversalwithStack(BinNode root);//栈实现非递归中序遍历
//	public void postordertraversal(BinNode node);// 后序遍历
//	public void postordertraversalwithStack(BinNode root);//栈实现非递归后续遍历
//	public void leveltraversalwithQueue(BinNode root);// 用队列实现层次遍历
//	// 用先序遍历和中序遍历序列创建二叉树。
//	public BinNodeImpl createBinTreebyPreandInOrder(List pre,List in);

二、辅助类

栈（自己编辑的）

// 把索引为0的位置作为栈尾,即栈中所有数据都是有效数据，属于不带头结点，即没有一个无效数据点
// 对于顺序栈而言，不会有线性表的插入删除操作需要花费O(n)的时间复杂度的问题，因为只会在栈顶插入
public class SStackwithoutHead implements SequentialStack
	private final static int DEFAULTSIZE = 10;
	private int size;	// 栈容量
	private Object[] stack;
	private int topIndex;	// 栈顶位置，从0索引，同时topIndex+1表示栈大小
	
	public SStackwithoutHead() 
		setup(DEFAULTSIZE);
	
	
	public SStackwithoutHead(int size) 
		setup(size);
	

	@Override
	public void setup(int sz)  // 初始化链式表
		size = sz;
		topIndex = -1;	// 不带头结点，所以初始化为topIndex为-1
		stack = new Object[sz];
	

	@Override
	public void push(Object ob) 
		if(topIndex<size)
			stack[++topIndex] = ob;// 先执行++topIndex
	

	@Override
	public Object pop() 
		if(!isEmpty())
			return stack[topIndex--];// 先执行stack[topIndex]
		else
			return null;
	

	@Override
	public Object topValue() 
		if(!isEmpty())
			return stack[topIndex];
		else
			return null;
	

	@Override
	public boolean isEmpty() 
		if(topIndex<0)
			return true;
		else
			return false;

队列（自己编辑的）

// 带头结点的队列
// 这里用头结点来避免逻辑循环数组中队满和队空问题
public class SQueuewithHead implements SequentialQueue
	private static final int DEFAULTSIZE = 4;
	private int front;// 队首
	private int rear;// 队尾
	private int size;// 队列容量
	private Object listArray[];// 队列
	public SQueuewithHead() 
		setup(DEFAULTSIZE);
	
	public SQueuewithHead(int sz) 
		setup(sz);
	
	@Override
	public void setup(int sz) 
		size = sz+1;// 带一个无效数据头结点
		front = 0;
		rear = 0;
		listArray = new Object[size];
	
	@Override
	public void enQueue(Object ob) 
		// 增加一个新元素到队尾,
		// 如果队尾的当前索引是size-1,即数组最后一个元素，那么下一个元素应当是在索引为0这个位置，
		// 那么可以用（++rear）%size
//		System.out.println(front+" \\t "+rear);
		if(front!=(rear+2)%size)// 判断非队满
			listArray[(++rear)%size] = ob;
	
	@Override
	public Object deQueue() 
		if(!isEmpty())return listArray[(++front)%size];// 出队一个队头元素
		return null;
	
	@Override
	public Object frontObject() 
		if(!isEmpty())return listArray[(front+1)%size];// 返回一个队头元素
		return null;
	
	public Object rearObject() 
		if(!isEmpty())return listArray[rear];// 返回一个队尾元素
		return null;
	
	@Override
	public boolean isEmpty() 
		if(front == rear) return true;
		return false;

ArrayList（JavaAPI的）

三、实现二叉树+先序遍历+中序遍历+后序遍历+用栈实现先序遍历+用栈实现中序遍历+用栈实现后序遍历+层次遍历+用队列实现层次遍历+用中序遍历和先序遍历确认二叉树

import java.util.List;

import com.zyx.queue.sequentialqueue.SQueuewithHead;
import com.zyx.stack.squentialstack.SStackwithoutHead;

public class BinNodeImpl implements BinNode
	private Object element;
	private BinNode left;
	private BinNode right;
	public BinNodeImpl() 
		element = null;
		left = null;
		right =null;
	
	public BinNodeImpl(Object ob) 
		element = ob;
		left = null;
		right = null;
	
	public BinNodeImpl(Object ob,BinNode leftnode,BinNode rightnode) 
		element = ob;
		left = leftnode;
		right = rightnode;
	

	@Override
	public Object getElement() 
		return element;
	

	@Override
	public void setElement(Object ob) 
		element = ob;
	

	@Override
	public BinNode getLeft() 
		return left;
	

	@Override
	public void setLeft(BinNode leftnode) 
		left = leftnode;
	

	@Override
	public BinNode getRight() 
		return right;
	

	@Override
	public void setRight(BinNode rightnode) 
		right = rightnode;
	

	@Override
	public boolean isLeaf() 
		return (left==null)&&(right==null);
	
	public void visit(Object ob) 
		System.out.print(ob);
	
	
	// 先序遍历，先访问根，再依次遍历左子树，再遍历右子树
	public void preordertraversal(BinNode root) 
		if(root!=null) 
			visit(root.getElement());
			preordertraversal(root.getLeft());
			preordertraversal(root.getRight());
		
	
	//栈实现非递归先序遍历
	public void preordertraversalwithStack(BinNode root)
		SStackwithoutHead stack = new SStackwithoutHead();
		BinNode node = root;
		// 当二叉树非空，压栈二叉树，并访问当前节点，开始遍历并访问左子树
		while(node!=null || !stack.isEmpty()) 
			if(node!=null) 
				stack.push(node);// 压栈
				visit(node.getElement());// 访问当前节点
				node = node.getLeft();// 开始向左遍历
			
			else //当左子树为空，出栈当前节点，并遍历右子树，如果右子树非空，压栈并访问右子树
				node = (BinNode) stack.pop();
				node = node.getRight();
			
		
	
	// 中序遍历，先遍历左子树，访问结点，再依次遍历右子树
	public void inordertraversal(BinNode node) 
		if(node!=null) 
			inordertraversal(node.getLeft());
			visit(node.getElement());
			inordertraversal(node.getRight());
		
	
	// 用栈实现非递归中序遍历。
	public void inordertraversalwithStack(BinNode root) 
		// 新建一个栈
		SStackwithoutHead stack = new SStackwithoutHead(10);
		BinNode node = root;// 指向下一个可能的栈顶元素
		while(node!=null || !stack.isEmpty()) 
			// 当二叉树非空，压栈二叉树，优先遍历左子树，即压栈左子树
			if (node!=null) 
				stack.push(node); // 压栈左子树
				node = node.getLeft();
			
			// 当左子树为空，出栈并访问当前节点，遍历右子树，如果右子树非空，压栈右子树
			else 
				// 出栈并访问该节点
				node = (BinNode) stack.pop();// 当左子树为空,出栈该节点
				visit(node.getElement());// 访问该节点
				node = node.getRight();// 遍历右子树
			
		
	
	// 后续遍历，先遍历左子树，再遍历右子树，最后访问根
	public void postordertraversal(BinNode node) 
		if(node!=null) 
			postordertraversal(node.getLeft());
			postordertraversal(node.getRight());
			visit(node.getElement());
		
	
	// 用栈实现非递归后续遍历
	// 这个比较复杂，如何在遍历到右子树为空后，然后出栈，出栈的可能是其左子树，也可能是当前节点，
	// 如何保证出栈以后，不会被再次压入？
	// 只要确保，四种情形出栈：一左空或右空时；二：左空右已出栈；三右空左已出栈
	// 对于栈而言，同一个元素不会被入栈两次。
	// 1.当结点第一次入栈时，设定其值为0，
	// 2.遍历左子树，
	// 3.当左子树为空或遍历结束时，将栈顶（分叉点）值设为1；
	// 4.遍历右子树，
	// 5.若右子树根节点非空，跳到步骤1；
	// 6.若右子树为空，栈顶值一定是1，开始进行出栈操作，直道最上层的分叉点,意味着这个分叉点的左子树遍历结束，
	// 7.跳转到3
	public void postordertraversalwithStack(BinNode root) 
		SStackwithoutHead stack1 = new SStackwithoutHead();
		SStackwithoutHead stack2 = new SStackwithoutHead();
		BinNode node = root;
		while(node != null || !stack1.isEmpty()) 
			while(node!=null) 
				stack1.push(node);
				stack2.push(0);
				node = node.getLeft();
			
			while(!stack1.isEmpty() && (int)stack2.topValue()==1) 
				visit(((BinNode) stack1.pop()).getElement());
				stack2.pop();
			
			if(!stack1.isEmpty()) 
				stack2.pop();
				stack2.push(1);
				node =((BinNode) stack1.topValue()).getRight();
			
		
	
	// 层次遍历：从第一层开始由左向右遍历，可以用一个队列来实现，将每一层的最左边作为队头，最右边作为队尾，队头先出队
	// 第一层：既是队头又是队尾，入队又出队
	// 1.如果
	
	public void leveltraversalwithQueue(BinNode root) 
		BinNode node = root;
		SQueuewithHead queue = new SQueuewithHead();
		queue.enQueue(node);
		while(!queue.isEmpty()) 
			node = (BinNode) queue.deQueue();
			visit(node.getElement());
			if(node.getLeft()!=null) 
				queue.enQueue(node.getLeft());
			
			if(node.getRight()!=null) 
				queue.enQueue(node.getRight());
			
		
	
	/**
	 * 由一种遍历序列无法构造唯一的二叉树
	 * 1)（后）先序遍历和中序遍历可以确定一棵二叉树；
	 * 2)后序遍历序列和先序遍历序列不可以确定一棵二叉树；
	 * 3)层次遍历序列和中序遍历序列也可以构造出一个二叉树。
	 */
	/**
	 * 在先序遍历中，第一个结点是根节点
	 * 在中序遍历中，根节点将二叉树分成两部分，左边是左子树，右边是右子树
	 * 对于中序遍历的左子树，先序遍历会有一个匹配的串，而先序遍历的串的第一个结点就是左子树的根节点，则右边就是右子树的串，
	 * 我们不需要匹配串，只要通过长度来匹配就行了。如：长度为n的中序遍历中，根节点索引为j，左子树：0->j-1,右子树：j+1->n-1
	 * 则左子树大小为j,右子树大小为n-j-1则先序遍历中左子树的位置在1->j,右子树的位置在j+1->n-j-1
	 * 如果左子树非空，则先序遍历中根节点后面的结点一定是左子树的根节点
	 * 如果右子树非空，则先序遍历中左子树遍历结束后的那个结点一定是右子树的根节点
	 * 如果左子树为空且右子树为空，则此结点，若在左边则是父节点的左子节点，若在右边则是父节点右子节点。
	 * 然后递归过程
	 */
	/**
	 * 
	 * 当中序遍历序列为空时，结束遍历
	 * 当中序遍历序列长度为1时，返回结果。
	 * 当中序遍历序列长度为2时，则必定至少有一个是父节点，一个是子节点，在左为左，在右为右
	 * 
	 */
	public BinNodeImpl createBinTreebyPreandInOrder(List pre,List in) 
		// 当中序遍历序列为空时，结束遍历
		if(in.isEmpty()) 
			return null;
		
		// 当中序遍历序列长度为1时，返回结果。
		if(in.size()==1) 
			return (new BinNodeImpl(in.get(0)));
		
		BinNodeImpl node=new BinNodeImpl(pre.get(0));// 获取根节点
		BinNodeImpl ltemp;
		BinNodeImpl rtemp;
		if(in.size()>1) 
			int j = 0;
			// 找到中序遍历根节点，索引为j，左子树：0->j-1,右子树j+1->in.size()-1
			// 先序遍历，左子树：1->j,右子树:j+1->pre.size()-1
			while (in.get(j)!=pre.get(0)) 
				j++;
			
			ltemp = createBinTreebyPreandInOrder(pre.subList(1,j+1),in.subList(0,j));
			rtemp = createBinTreebyPreandInOrder(pre.subList(j+1,pre.size()),in.subList(j+1,in.size()));
			node.setLeft(ltemp);
			node.setRight(rtemp);
			return node;
		
		return null;
	
	public BinNode createBinTreebyPostandInOrder(List pre,List list) 
		return (new BinNodeImpl());

四、测试结果

import java.util.ArrayList;

public class TestBinNode

	public static void main(String[] args) 
		BinNodeImpl root =new BinNodeImpl('A');
		root.setLeft(new BinNodeImpl('B'));
		root.getLeft().setRight(new BinNodeImpl('D'));
		root.setRight(new BinNodeImpl('C'));
		root.getRight().setLeft(new BinNodeImpl('E'));
		root.getRight().setRight(new BinNodeImpl('F'));
		root.getRight().getLeft().setLeft(new BinNodeImpl('G'));
		root.getRight().getRight().setLeft(new BinNodeImpl('H'));
		root.getRight().getRight().setRight(new BinNodeImpl('I'));
		System.out.println("\\n中序遍历");
		root.inordertraversal(root);
		System.out.println("\\n用栈实现非递归中序遍历");
		root.inordertraversalwithStack(root);
		System.out.println("\\n后续遍历");
		root.postordertraversal(root);
		System.out.println("\\n用栈实现非递归后序遍历");
		root.postordertraversalwithStack(root);
		System.out.println("\\n先序遍历");
		root.preordertraversal(root);
		System.out.println("\\n用栈实现非递归中序遍历");
		root.preordertraversalwithStack(root);
		System.out.println("\\n用队列实现层次遍历");
		root.leveltraversalwithQueue(root);
		@SuppressWarnings("rawtypes")
		ArrayList pre = new ArrayList();
		ArrayList in = new ArrayList();
		char pres[] = 'A','B','D','C','E','G','F','H','I';
		char ins[] = 'B','D','A','G','E','C','H','F','I';
		for(char c:pres) pre.add(c);
		for(char c:ins) in.add(c);
		System.out.println("\\n用先序遍历+中序遍历，确定二叉树。");
		BinNodeImpl node = (new BinNodeImpl()).createBinTreebyPreandInOrder(pre, in);
		System.out.println("\\n先序");
		root.preordertraversal(node);
		System.out.println("\\n中续");
		root.inordertraversal(node);
		System.out.println("\\n后续");
		root.postordertraversal(node);
		System.out.println("\\n层次");
		root.leveltraversalwithQueue(node);

运行结果：

中序遍历
BDAGECHFI
用栈实现非递归中序遍历
BDAGECHFI
后续遍历
DBGEHIFCA
用栈实现非递归后序遍历
DBGEHIFCA
先序遍历
ABDCEGFHI
用栈实现非递归中序遍历
ABDCEGFHI
用队列实现层次遍历
ABCDEFGHI
用先序遍历+中序遍历，确定二叉树。

先序
ABDCEGFHI
中续
BDAGECHFI
后续
DBGEHIFCA
层次
ABCDEFGHI

五、二叉树的应用

有一些特殊的应用（如线索二叉树）会增加一个指向父节点的指针，以便于向上搜索。增加一个父指针有点像在双链表中增加的指向前一节点的指针prev。实际上，父指针通常是不必要的，并且增加了许多结构性开销。

在利用指针实现的二叉树中，叶结点与分支结点是否使用相同的类定义十分重要。有一些应用只需要用叶节点存储数据。还有一些应用要求分支结点与叶节点存储不同类型的数据。根据二叉树的定义，只有分支结点有非空子节点。因此，分别定义分支结点与叶结点将节省存储空间。

如表达式二叉树。如下图表示的。页结点与分支结点是不同的，分支节点存储元素数目很少的操作符集合中的一个操作符，因此分支结点可以存储这个操作符的代码或者用一个字符存储其图形符号。叶结点则存储不同的变量或数值，所以叶节点必须有足够大的数据区来存储各种可能的值。同时，叶节点不必存储子节点指针（因为其就算有，也都是空指针）。

分支结点

public class BranchNode implements BinNode
	private BinNode left; // 左子节点
	private BinNode right;// 右子节点
	private Character opx; // 操作符
	public BranchNode(Character operator,BinNode leftNode,BinNode rightNode) 
		opx = operator;left=leftNode;right=rightNode;
	
	@Override
	public Object getElement() return opx;
	@Override
	public void setElement(Object ob) opx=(Character)ob;
	@Override
	public BinNode getLeft() return left;
	@Override
	public void setLeft(BinNode leftnode) left = leftnode;
	@Override
	public BinNode getRight() return right;
	@Override
	public void setRight(BinNode rightnode) 
	@Override
	public boolean isLeaf() return false;

叶节点

public class LeafNode implements BinNode
	public String var;
	public LeafNode(String val) 
		var=val;
	
	@Override
	public Object getElement() return var;
	@Override
	public void setElement(Object ob) var=(String)ob;
	@Override
	public BinNode getLeft() return null;
	@Override
	public void setLeft(BinNode leftnode) 
	@Override
	public BinNode getRight() return null;
	@Override
	public void setRight(BinNode rightnode) 
	@Override
	public boolean isLeaf() return true;

测试遍历：用中序遍历可以形式上实现运算。

public class TestBranchandLeaf 
	public static void traverse(BinNode node) 
		if(node==null)return;
        // 通过node.isLeaf()判断结点的类型，从而给出真正的结点类型。
		if(node.isLeaf())System.out.print(node.getElement());
		else 
			traverse(node.getLeft());
			System.out.print(node.getElement());
			traverse(node.getRight());
		
	
	public static void main(String[] args) 
		LeafNode leaf1 = new LeafNode("4");
		LeafNode leaf2 = new LeafNode("x");
		BranchNode node1 = new BranchNode('*', leaf1, leaf2);
		LeafNode leaf3 = new LeafNode("2");
		LeafNode leaf4 = new LeafNode("x");
		BranchNode node2 = new BranchNode('*', leaf3, leaf4);
		LeafNode leaf5 = new LeafNode("a");
		BranchNode node3 = new BranchNode('+',node2, leaf5);
		BranchNode node4 = new BranchNode('*', node1, node3);
		LeafNode leaf6 = new LeafNode("c");
		BranchNode node5 = new BranchNode('-', node4, leaf6);
		traverse(node5);

运行结果：

4*x*2*x+a-c

六、空间开销

二叉树总共N个结点，从分支结点来看，设有0个子节点的结点有N0个，只有一个子节点的结点有N1个，有2个子节点的结点有N2个，N=N0+N1+N2；从子节点来看，有2个子节点的结点一共有2*N2个子节点，只有1个子节点的结点总共有N1个子节点，有0个子节点的结点一共有0个子节点，还有一个根节点，N=0+N1+2*N2+1；则N0=N2+1。

满二叉树定理：非空满二叉树的叶节点数等于其分支节点数加1。

证明：满二叉树，只有1个子节点的结点有0个，N1=0，故分支节点是N2个。

一棵非空二叉树空子树的数目等于其结点数目加1。

证明：有0个子节点的结点有N0个，即有2个null子节点的结点有N0个，有2*N0个null结点，有1个子节点的结点有N1个，即有1个null子节点的结点有N1个，即2*N0+N1=N0+N1+N2+1=N+1个null结点。

结构性开销是指为了实现数据结构所花费的空间，即那些不用来存储数据的空间。结构性开销的大小取决于很多因素，包括哪些结点存储数据（全部结点或只是叶节点），是否有父指针，以及是否是满二叉树等。

如上面的一般二叉树中，结构性开销是N+1。

如果只是叶节点存储数据，那么结构性开销在全部开销中占有的比例取决于二叉树是否“满”，如果二叉树不满，有可能在一串分支结点后只有一个叶节点。

如果每个结点都实现为存储2个子节点指针和1个数据，每个结点指针需要空间 p，每个数据需要空间 d ，那么有n个结点的二叉树，一共需要空间n(2p+d)，那么共有null指针n+1个，即结构性开销为(n+1)2p，省略1来计算，结构性占比大约：

如果p=d，那就意味着结构性开销将达到全部空间的约一半。

如果只有叶节点存储有效数据的满二叉树，设叶节点数有t个，那么根据非空满二叉树定理，叶节点有t个，分支结点有t-1个，近一半的“数据区”没有使用到。

对于只有叶结点存储数据的满二叉树，比较好的处理办法是：分支节点只存储两个指针，没有数据区，分支结点占空间2pt，叶节点只有一个数据区，而没有指针，叶节点占空间d(t+1)，总共需要开销2pt+d(n+1)，如果p=d，结构性开销约为

七、使用数组实现完全二叉树

完全二叉树常被用于堆数据结构，堆经常被用来实现有优先队列和外排序算法。完全二叉树具有从上到下，从左到右依次排列的结构，可以直接用数组存储二叉树的数据。从上层可以直接根据父节点的位置判断出左子节点和右子节点的索引。这就意味着，对有n个结点的二叉树使用大小为n的数组来实现，就不存在结构性开销。

对于所有二叉树：

h从1计，有i层表示高度为i。

对于完全二叉树：其要么是满二叉树，要么是满二叉树差一个叶节点，所以其很容易受用满二叉树的定理（叶节点数是分支结点的数目加一）。从完全二叉树的结构上，容易知道：

完全二叉树如果结点数目是奇数，那么这个二叉树一定是满二叉树；

如果是偶数，那么这个二叉树的最后一层最后一个结点一定是左子节点，只要增加一个右子节点，那么它又是满二叉树。

也就是说，设分支结点数为t，如果结点数n=2t+1是奇数，那么最后一个分支结点的索引是t-1=(n-1)/2-1=floor(n/2)-1;如，结点数为3，那么分支结点只有1个（根节点），那么最后一个分支结点的索引是0=(3-1)/2-1.

如果结点数n=2t是偶数，那么增加一个右子节点，n+1=2t+1，成为满二叉树,最后一个分支结点的索引是t-1=n/2-1=floor(n/2)-1。如，结点数为4，那么分支结点有2个，那么最后一个分支结点的索引是1=4/2-1=floor(4/2)-1=1.

又完全二叉树最后一个分支结点一定是最后一个结点的父节点，则第n个结点其父节点索引一定是floor(n/2)-1，由于在Java计算时，对整数计算自动向下取整，所以，第n个结点的父节点索引就是n/2-1.

那么索引为t的结点是

n个结点：树中节点的索引是0~n-1

对于根节点，没有左兄弟节点，右兄弟节点，父节点。

对于索引为r的结点，其所处的层数（根节点在第一层）是。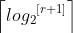

八、二叉排序树==二叉检索树==BST

8.1 BST基础概念

二叉树的数据结构比之线性表的差别在BST（Binary Search Tree）表现得很明显。

在一个没有顺序的链表中根据城市的名称，查找一条特殊记录的平均检索时间为θ(n)。对于一个大型数据库，显得太慢了。

在一个有顺序的链表中进行检索，并不会因为是“有顺序的”就提高了检索速度。

如果线性表使用有序数组实现，那么使用二分法减速只需要θ(log n)。但是插入需要时间θ(n)。

也就是对于线性表，没有办法实现检索和插入都能很快完成，但BST却可以实现。

定义：二叉检索树（Binary Search Tree,BST）的任何一个结点，设其值为K，则该节点左子树中任意一个结点的值都小于K。该节点右子树中任一个结点的值都大于或等于K。

特点：如果按照中序周游将各个结点打印出来，就会得到由小到大的排列。

与一般二叉树的区别在于，BST是基于一般二叉树结构的接口类型 BinNode，这样就不用顾虑到与二叉树的实现 BinNodeImpl 包括的可以修改左子树、右子树和结点属性的功能的冲突，因为其不能被实现，BST本身就是限制了一般二叉树的功能，将其赋予特殊的使命，就好像栈和队列都属于线性表，但是它们都被限制了功能，且根据自身特性增加修改了功能：

增加了插入结点的功能；
增加了删除结点的特殊功能；
增加了有检索意义的检索功能。

创建BST

插入结点4、14和15.

从节点值等于10的位置开始获取最小值

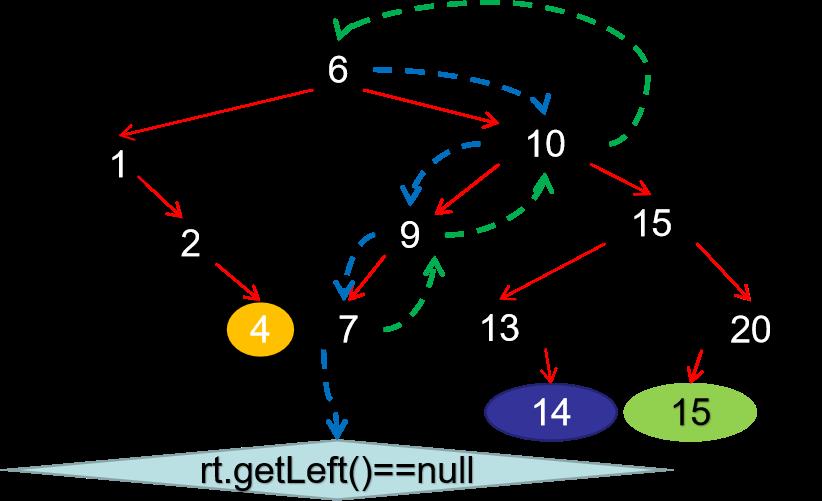
删除结点值为13的结点

8.2 数据对象

用一个对象来存储结点值，其中可以设置其他值，但是key值用作大小值。

public interface Elem 
	public abstract int key();

public class ElemImpl implements Elem
	private int key;
	public ElemImpl(int val) 
		key = val;
	
	@Override
	public int key() 
		
		return key;

8.3 实现BST的插入、删除、获取最小值、删除最小值、周游BST的功能

import com.zyx.bintree.BinNode;
import com.zyx.bintree.BinNodeImpl;

public class BST 
	private BinNode root;
	public BST() root=null;
	public BinNode getRoot() 
		return root;
	
	public void clear(BinNode root) root=null;
	// 在BST中插入一个结点
	public void insert(Elem val) root = insertImpl(root,val);
	// 删除BST中的一个结点
	public BinNode remove(int key) return removeImpl(root,key);
	// 查找BST中的一个结点
	public Elem find(int key) return findImpl(root,key);
	// 判断是否为空
	public boolean isEmpty() return root==null;;
	// 查找功能实现：通过递归实现
	public Elem findImpl(BinNode rt,int key) 
		if(rt==null) return null; // 当二叉树为空，结束递归
		Elem it = (Elem)rt.getElement();
		if(it.key()>key) return findImpl(rt.getLeft(), key);// 当根节点值比 K值大，向左递归
		else if(it.key()==key) return it;  //当根节点值与K等大时，返回结果
		else return findImpl(rt.getRight(), key);// 当根节点值比K值大时，向右遍历
	
	// 插入功能的实现，通过递归实现:大或等向右，小向左
	public BinNode insertImpl(BinNode rt,Elem val) 
		// 当二叉树为空，返回一个二叉树结点
		if(rt==null) return new BinNodeImpl(val);
		// 当二叉树非空，根据根节点的值断定左递归还是右递归
		Elem it = (Elem)rt.getElement();
		// 当插入的值比根节点小,向左递归
		if(it.key()>val.key()) rt.setLeft(insertImpl(rt.getLeft(), val));
		// 其他情形右转
		else
			rt.setRight(insertImpl(rt.getRight(), val));
		return rt;
	
	// 删除功能实现
	// 先要找到这个值所在的节点R，然后对这个值的子树进行处理
	// 1. R没有子节点，那么将R的父节点指向它的指针改为null
	// 2. R有一个子节点，那么就把父节点指向R的指针改为指向R的子节点
	// 3. R有2个子节点，一种是用左子树的最右边的结点来替代它，一种是用右子树的最左边的结点来替代它，替代需要先删除这个用来替代的结点，然后将其值赋给R
	// 如果为空，即找不到，那么返回空
	
	// 通过递归来实现
	// 递归结束条件：1. BST为空 2. 找到了这个节点
	// 递归执行过程：K值小于当前结点值则向左转，K值大于当前节点值则向右转，K值等于当前节点值则结束递归。
	public BinNode removeImpl(BinNode rt,int key) 
		if(rt==null) return null;
		Elem it = (Elem)rt.getElement();// 获取节点值
		// 遍历找到这个节点
		// 这里有一个问题，为什么加上setLeft与setRight呢?而不是直接removeImpl(rt.getLeft（），key)?
		// 答：是因为，在递归回溯的时候，有两种可能：
		// 1.是直接对传入的对象地址的值进行了修改，地址未变. 可以看到后面由于有一个删除结点的过程，所以子节点的地址会被修改，所以地址变了
		// 2.传入对象的地址被修改了，返回的是修改后的子树rt的值。
		if(key<it.key())rt.setLeft(removeImpl(rt.getLeft(), key));
		else if(it.key()<key)rt.setRight(removeImpl(rt.getRight(), key));
		// 当找到了这个节点rt,根据上面的三种情形进行处理
		else 
			// 当rt左子树为空，把父指针指向rt的指针改为指向rt的右子树
			if(rt.getLeft()==null) 
				rt = rt.getRight();
			
			// 当rt右子树为空，把父指针指向rt的指针改为指向rt的左子树
			else if(rt.getRight()==null) 
				rt = rt.getLeft();
			
			// 当子树都不为空，用右子树的最左边（最小值）的结点getMin来替代它，替代需要先删除这个用来替代的结点，然后将其值赋给rt
			else
				rt.setElement((Elem) getMin(rt.getRight())); // 设置rt值为右子树最小结点值
				rt.setRight(deleteMin(rt.getRight()));
			
		
		// 返回修改后的值
		return rt;
	
	// 此处突然想到两个问题：Java的参数传递的对象，它传进去的一定是地址，过经过递归，那么这个地址就一定要被修改
	// 如果递归结构，如二叉树的递归的地址，如return getMin(地址)和函数参数的地址，如public BinNode getMin(地址)是一样的，
	// 即都是BinNode rt,就会造成无限循环
	// Java的赋值运算符对对象进行赋值是将地址复制给对方，
	// 如果递归运算传递的对象是同一个，则一直对同一个对象进行操作，
	// 如果非递归运算中不停的用【地址B=地址A.left】这样子迭代，而最终返回的是地址B，则返回的就不是原对象了，而是最底层的对象，
	// 		如果在一开始就用一个副本了,如【地址A.副本=地址A】,那么最后只需要返回【地址A.副本】
	/**
	 * 以返回值递归，那么最终的返回值，就会是先遍历到最深层，然后将最深层的结果，从最深层传到最顶层。
	 * @param rt		BST
	 * @return			最小值的结点的值 
	 */
	public Elem getMin(BinNode rt) 
		// 当树左子树为空时，返回子树,结束递归
		if(rt.getLeft()==null) 
			return (Elem) rt.getElement();
		
		// 当树左子树非空时，开始向左递归
		else 
			return getMin(rt.getLeft());
		
	
	// 当左子树非空，向左递归，当左子树为空时，返回右子树根节点，开始回头，
	// 通过rt.setLeft()将最左节点的右子节点作为父节点的左子节点，从最深层依次向上执行完毕deleteMin，并执行rt.setLeft()
	// 然后返回rt,依次向上执行，即从底到根,执行一遍rt.setLeft()。
	// 如果rt没有左子树，则右子树的根节点将作为根节点
	/**
	 * 
	 * @param rt 	要修改的BST
	 * @return 		修改后的BST
	 */
	public BinNode deleteMin(BinNode rt) 
		if(rt.getLeft()==null) 
			return rt.getRight();
		
		else 
			rt.setLeft(deleteMin(rt.getLeft()));
			return rt;
		
	
	// 通过中序遍历将BST从小到大打印出来。
	public void printBST(BinNode rt,int level) 
		if (rt==null) return;
		printBST(rt.getLeft(), level+1);
		for(int i = 0;i<level;i++) 
			System.out.print("  ");
		
		System.out.println(((Elem)rt.getElement()).key());
		printBST(rt.getRight(), level+1);

测试BST的实现

public class TestBST 
	public static void main(String[] args) 
		BST bst = new BST();
		int[] nums = 6,1,2,10,9,7,15,13,20;
		for(int n:nums) 
			bst.insert((new ElemImpl(n)));
		
		bst.printBST(bst.getRoot(), 0);
		System.out.println("*********************");
		bst.insert(new ElemImpl(4));
		bst.insert(new ElemImpl(14));
		bst.insert(new ElemImpl(15));
		bst.printBST(bst.getRoot(), 0);
		System.out.println("*********************");
		bst.remove(13);
		bst.printBST(bst.getRoot(), 0);

运行结果

1
2
6
7
9
10
13
15
20
*********************
1
2
4
6
7
9
10
13
14
15
15
20
*********************
1
2
4
6
7
9
10
14
15
15
20

BST比起链表实现了检索和插入速度一起提升的效果，但是BST容易出现不平衡的情况。如第一个插入的值是6，后面插入的值都是比6大的值，那么这些值都会出现在右子树，而左子树特别空，出现严重不平衡。

如果二叉树是平衡的，则有n个结点的二叉树高度大约为log n。但如果二叉树出现完全不平衡，则高度可以达到n。因为平衡二叉树每次操作的平均时间代价为θ(log n)，而严重不平衡二叉树最差情况下平均每次操作代价为θ(n)。

假设每次一个一个地按照插入的方式创建一棵有n个结点的BST，并且很幸运地遇到了每个结点的插入都保持平衡的情况（“随机”的顺序很可能实现这种目的），那么每次插入的平均时间代价为，总共为。如果接点按递归顺序插入，就会得到一条高度为n的链，插入的时间代价为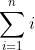，也即。

九、平衡二叉树——Balanced Binary Tree——AVL

平衡二叉树 AVL，任意节点的平衡因子（左子树高度-右子树高度）的绝对值不超过一。

9.1 如何确定是否平衡二叉树

import com.zyx.bintree.BinarySearchTree.Elem;
import com.zyx.bintree.basicbinnode.BinNode;
import java.lang.Math;
public class AVL 
	private BinNode root;
	private boolean balanced=true;
	public AVL(BinNode rt) 
		root = rt;
	
	public BinNode getRoot() 
		return root;
	
	public int height() return heightImpl(root);
	public boolean isBalanced() 
		heighthelp_isbalanced(root);
		return	balanced;
	
	// 获取二叉树的高度
	// 后序遍历是先遍历到底，然后利用回溯过程来计算。后续遍历过程，可参考图片,后序遍历.png
	// 当结点为空，高度为0，也就是叶结点的子节点，高度都设为0，而不是相对整棵树的高度
	// 在遍历过程中，肯定会遍历到每个结点
	// 叶节点4的两个子节点是0和0，则回溯叶节点4，h=1，同理5,6，h=1
	// 由于4，5,h=1，则结点2，h=2
	// 由于6，h=1，结点3的右子节点，h=0，结点3高度为1,
	// 由于2,3，h=2，则结点1，h=3
	public int heightImpl(BinNode rt) 
		// 获取二叉树的高度
		if(rt==null) 
			return 0;
		
		int left_h = heightImpl(rt.getLeft());
		int right_h= heightImpl(rt.getRight());
		return (left_h > right_h)?(1+left_h):(1+right_h);
	
	// 判断是否是平衡二叉树
	// 根据平衡二叉树的定义，平衡二叉树的每个结点都有一个平衡因子参数，|左子树高度-右子树高度|<=1
	// 所以每一个结点都要考察，所以这又是一个遍历过程。上层基于下层，所以还是使用后序遍历
	// 如果要考虑使用层次遍历的话，那么就必须考虑哪些结点属于哪一层，且执行是从上到下，无法实现。
	// 为了避免重复计算高度的遍历过程，我们可以利用计算高度的过程,
	// 其实为了在找到第一个[平衡因子>1]时，立刻退出，可以用栈来实现非递归过程
	public int heighthelp_isbalanced(BinNode rt) 
		if(rt==null) return 0;
		int left_h = heighthelp_isbalanced(rt.getLeft());
		int right_h = heighthelp_isbalanced(rt.getRight());
		if(Math.abs(left_h-right_h)>1) 
			System.out.println("不平衡结点："+((Elem)rt.getElement()).key());
			balanced = false;
		
		return Math.max(left_h,right_h)+1;

测试代码：

import com.zyx.bintree.BinarySearchTree.BST;

public class TestAVL 

	public static void main(String[] args) 
		// 用一个BST来测试下，参看图片BST.png。结果应该是4
		int[] nums = 6,1,2,10,9,7,15,13,20;
		BST bst = new BST(nums);
		bst.printBST(bst.getRoot(), 0);
		AVL avl = new AVL(bst.getRoot());
		System.out.println("height："+avl.height());
		System.out.println("isbalanced："+avl.isBalanced());

测试结果：

1
2
6
7
9
10
13
15
20
height：4
isbalanced：true

以上是关于N日一篇——二叉树的主要内容，如果未能解决你的问题，请参考以下文章

N日一篇——二叉树

二叉树的特性

树与二叉树

心里没点B树，怎能吃透数据库索引底层原理？

二叉树知识总结

堆排序详解