分类和回归-决策树算法(ID3C4.5和CART)
Posted 吾仄lo咚锵
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了分类和回归-决策树算法(ID3C4.5和CART)相关的知识,希望对你有一定的参考价值。
文章目录
简介
决策树(Decision Tree)是⼀种树形结构,每个节点表示⼀个属性上的判断,每个分⽀代表⼀个判断结果的输出,最后每个叶节点代表⼀种分类结果,本质是⼀颗由多个判断节点组成的树。
类似if-else结构,通过若干判断(决策)来确定分类结果,比如打网球数据集中,包括天气、温度、湿度、风力四个特征,标签是play,表示是否适合打网球,属于二分类问题。
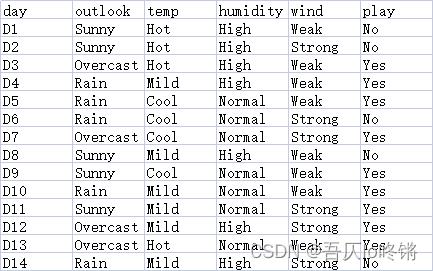
那我们便可以通过如下决策树进行预测是否适合打网球,先判断天气,再判断温度······,树中中间结点表示决策条件,叶子节点表示决策结果。
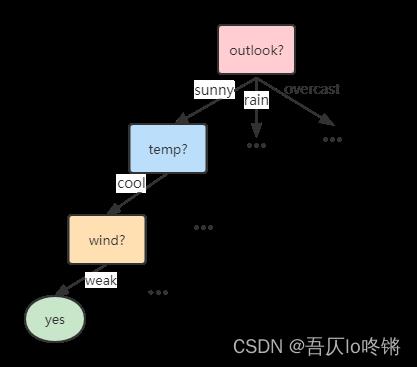
但是一个显然的问题是,我们应该如何确定判断条件的先后?比如上图中是先判断天气,若天气晴天再判断温度,再判断风力等,如果交换判断条件,将会直接影响分类结果。也就是我们需要定义划分依据,确定当前使用哪个特征值来作为划分依据,有了划分依据便可以构建决策树。划分依据包括ID3算法、C4.5算法和CART算法。
划分依据
ID3算法
ID3算法全称Iterative Dichotomiser 3,使用信息增益来作为划分依据,信息增益(information gain)就是划分数据集前后熵(information entropy)的差值。
物理学中,熵用来度量混乱程度。也就是说,熵越大则越乱,熵越小则越有序。我们希望决策条件划分出来的结果尽可能的属于同一类,即结点的“纯度”越来越高。
假设样本集合 D D D共有 N N N类, p k p_k pk表示样本集合 D D D中第 k k k类样本所占比例, D D D的信息熵 H ( D ) H(D) H(D)的定义如下:
H
(
D
)
=
−
∑
k
=
1
N
p
k
l
o
g
2
p
k
H(D)=-\\sum_k=1^Np_klog_2p_k
H(D)=−k=1∑Npklog2pk
由于比例
p
k
p_k
pk取值(0,1),而log函数在(0,1)间为负,添加负号,使熵的值为正。
H
(
D
)
H(D)
H(D)的值越小,则
D
D
D的纯度越高。
比如对于outlook特征值,14天中有5天Sunny、5天Rain、4天Overcast,则
H
(
o
u
t
l
o
o
k
)
=
−
(
5
14
l
o
g
2
5
14
+
5
14
l
o
g
2
5
14
+
4
14
l
o
g
2
4
14
)
=
1.58
H(outlook)=-(\\frac514log_2\\frac514+\\frac514log_2\\frac514+\\frac414log_2\\frac414)=1.58
H(outlook)=−(145log2145+145log2145+144log2144)=1.58
特征
A
A
A对数据集
D
D
D的信息增益
G
(
D
,
A
)
G(D,A)
G(D,A),定义为集合
D
D
D的信息熵
H
(
D
)
H(D)
H(D)与特征
A
A
A给定条件下
D
D
D的信息条件熵
H
(
D
∣
A
)
H(D|A)
H(D∣A)之差,即:
G
a
i
n
(
D
,
A
)
=
H
(
D
)
−
H
(
D
∣
A
)
=
H
(
D
)
−
∑
v
=
1
V
∣
D
v
∣
∣
D
∣
H
(
D
v
)
Gain(D,A)=H(D)-H(D|A)=H(D)-\\sum_v=1^V\\frac|D_v||D|H(D_v)
Gain(D,A)=H(D)−H(D∣A)=H(D)−v=1∑V∣D∣∣Dv∣H(Dv)
其中特征 A A A有 V V V个取值,即用 A A A对数据集 D D D来划分会产生 V V V个分支,用 D v D_v Dv表示第 v v v个分支中数据集 D D D在特征 A A A上取到第 v v v个值的样本。信息增益表示得知特征X的信息⽽使得类Y的信息熵减少的程度。
比如特征
o
u
t
l
o
o
k
outlook
outlook取值
s
u
n
n
y
sunny
sunny时,5天
s
u
n
n
y
sunny
sunny中有2天正例(yes,适合打网球),3天负例,则
H
(
o
u
t
l
o
o
k
s
u
n
n
y
)
=
−
(
2
5
l
o
g
2
2
5
+
3
5
l
o
g
2
3
5
)
=
0.97
H(outlook_sunny)=-(\\frac25log_2\\frac25+\\frac35log_2\\frac35)=0.97
H(outlooksunny)=−(52log252+53log253)=0.97
同理有:
H
(
o
u
t
l
o
o
k
r
a
i
n
)
=
−
(
3
5
l
o
g
2
3
5
+
2
5
l
o
g
2
2
5
)
=
0.97
H(outlook_rain)=-(\\frac35log_2\\frac35+\\frac25log_2\\frac25)=0.97
H(outlookrain)=−(53log253+52log252)=0.97
H
(
o
u
t
l
o
o
k
o
v
e
r
c
a
s
t
)
=
−
(
4
4
l
o
g
2
4
4
+
0
0
l
o
g
2
0
0
)
=
0
H(outlook_overcast)=-(\\frac44log_2\\frac44+\\frac00log_2\\frac00)=0
H(outlookovercast)=−(44log244以上是关于分类和回归-决策树算法(ID3C4.5和CART)的主要内容,如果未能解决你的问题,请参考以下文章