Graph Representation Learning学习笔记-chapter5
Posted Dodo·D·Caster
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Graph Representation Learning学习笔记-chapter5相关的知识,希望对你有一定的参考价值。
Chapter5 The Graph Neural Network Model
之前的章节是为每个节点生成嵌入,而此章为整个图结构的节点生成嵌入,更为复杂
Permutation invariance
- means that the function does not depend on the arbitrary ordering of the rows/columns in the adjacency matrix
permutation equivariance
- means that the output of f is permuted in an consistent way when we permute the adjacency matrix.
Input
- graph G = ( V , E ) G = (V,E) G=(V,E)
- node features X ∈ R d × ∣ V ∣ X \\in R^d \\times |V| X∈Rd×∣V∣
generate
- node embedding z u , ∀ u ∈ V z_u, \\forall u \\in V zu,∀u∈V
5.1 Neural Message Passing
GNN每一轮消息传递中,节点u的隐藏嵌入: h u ( k ) h_u^(k) hu(k)
- 表示每一个节点u都根据邻居的聚合信息进行更新
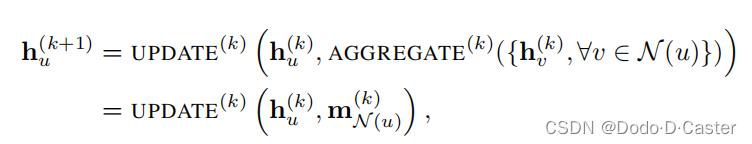
- k=0时, h u ( 0 ) = X u h_u^(0)=X_u hu(0)=Xu,也就是第一轮开始前,h为输入的节点特征
- k=i时,聚合邻居信息和本身信息更新下一轮的输入(聚合了 i-hop neighborhood 的信息)
- k=K时,输入最后一层的结果作为每一个节点的嵌入 z u = h u ( K ) z_u=h_u^(K) zu=hu(K)
特点
- 聚合了结构信息
- 基于特征
CNNs:从图像中spatially-defined patches聚合特征信息
GNNs:基于local graph neighborhoods聚合信息
basic GNN
basic GNN message passing(node-level equations):
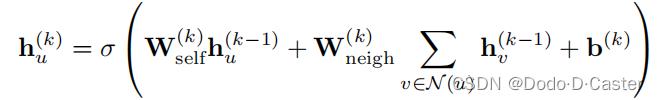
- h ( k ) h^(k) h(k) 代表可训练的参数矩阵
- σ 代表一个非线性的函数,如tanh或ReLU
- b ( k ) b^(k) b(k) 代表 bias term
basic GNN message passing

- H ( t ) H^(t) H(t) 代表t层节点的表示矩阵
- A 代表邻接矩阵
步骤
- 累加邻居信息
- 线性结合自身信息(previous embedding)
- 应用elementwize non-linearity
将basic GNN用UPDATE 和 AGGREGATE的形式表示:


self-loop GNN

- update函数已经在aggregate过程中被定义
basic GNN的self-loops表示(graph-level) : H ( t ) = σ ( ( A + I ) H ( t − 1 ) W ( t ) ) H^(t)= σ ((A+I)H^(t-1)W^(t)) H(t)=σ((A+I)H(t−1)W(t))
5.2 Generalized Neighborhood Aggregation
推广和改进basic GNN的AGGREATE
neighborhood normalization
采用 累加邻居的嵌入 m N ( u ) = ∑ v ∈ N ( u ) h v m_N(u)= \\sum _v \\in N(u) h_v mN(u)=∑v∈N(u)hv 的方式进行聚合的问题:
- 有时会不稳定
- 对节点的度高度敏感
改进方法1:用平均的方式代替累加
- m N ( u ) = ∑ v ∈ N ( u ) h v ∣ N ( u ) ∣ m_N(u)=\\frac \\sum _v \\in N(u) h_v |N(u)| mN(u)=∣N(u)∣∑v∈N(u)hv
改进方法2:symmetric normalization
- m N ( u ) = ∑ v ∈ N ( u ) h v ∣ N ( u ) ∣ ∣ N ( v ) ∣ m_N(u)=\\sum _v \\in N(u) \\frac h_v \\sqrt|N(u)||N(v)| mN(u)=∑v∈N(u)∣N(u)∣∣N(v)∣hv
Graph convolutional networks (GCNs)
apply : symmetric-normalized aggregation + self-loop update approach
message passing function:
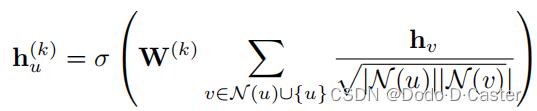
规范化的问题
- 结构特征会损失
Pooling
池化技术可以提升性能,将多个节点变成一个节点
Janossy pooling
不同于其他方法,它对邻居的排列顺序敏感

- Π 代表一个排列集合
- ρ φ ρ_φ ρφ 代表排列敏感函数
两种方法:
- 在每一次运用aggregator时,对可能的排列进行随机采样,采样的结果是一个随机的子集
- 对领域的节点进行规范排序(按度降序排序,with ties broken randomly)
Neighborhood Attention
基本思想:给每一个邻居分配一个注意力权重,用来权衡这个邻居在聚合中的影响
Graph Attention Network (GAT)
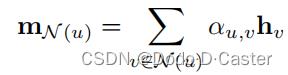
- α u , v \\alpha _u,v αu,v:对u节点进行聚合的时候邻居v的注意力
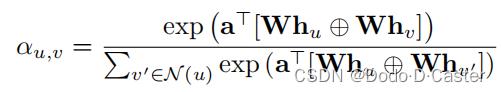
- α \\alpha α:可训练的注意力向量
- W:可训练的矩阵
- ⊕:连接操作
不同的注意力函数:
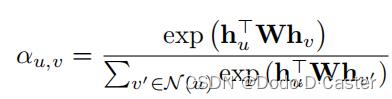
- 包含bilinear attention model

- 使用MLPs
5.3 Generalized Update Methods
over-smoothing:经过多轮消息传递后,图中所有节点的表征会变得相似
- 当node-specific信息在几次消息传递后被”washed out”或”lost”时,会发生over-smoothing(也就是说,节点在update的时候过度依赖当前层的邻居信息,而忽略了先前层的信息)
- 缓减方法:尝试在update时直接保存之前几轮消息传递的信息
- use concatenations and skip-connection methods
度量u节点对v节点的影响的方法:examining the magnitude of the corresponding Jacobian matrix
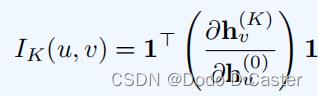
1:a vector of all ones
定理:对于任意使用self-loop update方法和有着下面形式的聚合函数的GNN
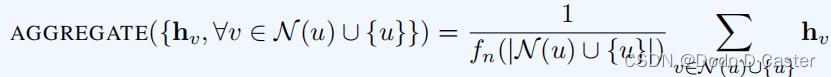
我们有:
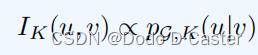
pG,K(u|v) 代表从节点u开始,长度为K的随机walk后,访问了节点v的可能性
最简单的skip connection update方法采用一个连接(concatenation)来在消息传递过程中保存更多的node-level信息:
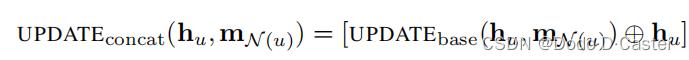
其他skip connection update方法:
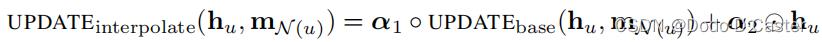
- α 1 , α 2 ∈ [ 0 , 1 ] d α_1, α_2 ∈ [0, 1]^d α1,α2∈[0,1]d : gating vectors
- ◦ 表示elementwise multiplication
Gated updates
从RNN上提取灵感:
- 用节点的hidden state代替hidden state argument of the RNN update function( h ( t ) h^(t) h(t))
- 用从本地邻居聚合的信息代替观察矩阵( x ( t ) x^(t) x(t))
该方法在deep GNN architectures(超过10层)和防止过平滑上十分有效
jumping knowledge connection
防止过平滑:利用每一层消息传递的表征而不仅使用最后一层的输出
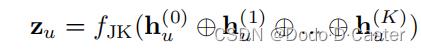
- z u z_u zu 为最后一层的节点表示
- f J K f_JK fJK 是任意的可微函数
5.4 Edge Features and Multi-relational GNNs
处理多关系图或异构图的方法
Relational Graph Neural Networks (RGCN)
方法:为每个关系类型制定单独的转换矩阵(transformation matrix)
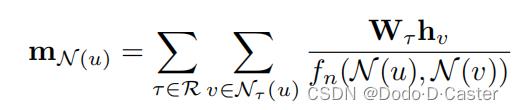
-
f
n
f_n
fn:归一化函数
- 既依赖节点u的neighborhood
- 又依赖被聚合的邻居v
- 缺点:参数的数量会快速增长
- 会导致过拟合和学习速度慢
解决方法:basis matrix approach : parameter sharing with basis matrices
basis matrices:
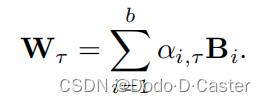
- B i B_i Bi:basis matrix
- α i , τ \\alpha_i,τ αi,τ:特定关系的参数
aggregation function:
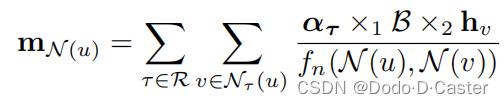
- α τ \\alpha_τ ατ:包含关系τ的basis combination weights
RGCN:学习每个关系的嵌入,以及在所有关系中共享的tensor
Attention and feature concatenation
利用attention中边的特征(或者在消息传递过程中将边的特征与邻居的嵌入连接)来重新定义一个aggregate函数 A G G R E G A T E b a s e AGGREGATE_base AGGREGATEbase
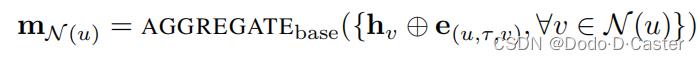
5.5 Graph Pooling
目标:为了学习整个图的嵌入,pool together node embeddings
- 设计一个池化函数 f p f_p fp将节点嵌入集合( z 1 , z 2 , . . . , z ∣ v ∣ z_1,z_2,...,z_|v| z1,z2,...,z∣v∣)表征为整个图的嵌入( z G z_G zG)
通过set pool的方式来学习graph-level嵌入
- 方法1:对节点嵌入做累加或取平均

- $f_n$:归一化函数
- 方法2:结合LSTMs和attention来pool节点嵌入
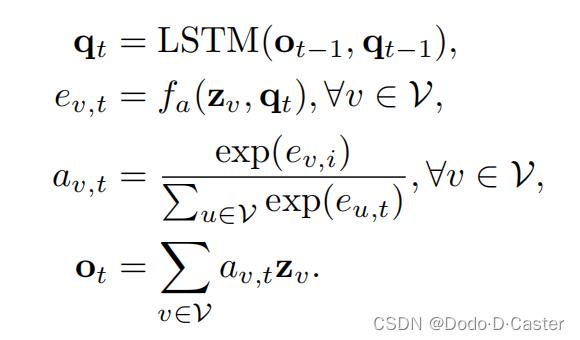
- $q_t$:a query vector for the attention at each iteration t
- 用来计算每个节点的注意力得分
- 步骤:
- 计算每个节点的注意力得分
- 将得分归一化
- 基于得分按权重累加节点嵌入
- 用累加的结果和LSTM来更新query vector
graph coarsening 图粗化
图池化的缺点:没有考虑图的结构

- 解决方法:graph clustering or coarsening
聚类函数:
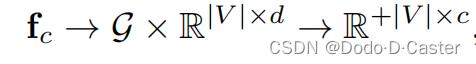
- 该函数会生成一个聚类分配矩阵(cluster assignment matrix)
-
S
以上是关于Graph Representation Learning学习笔记-chapter5的主要内容,如果未能解决你的问题,请参考以下文章
-
S