读《趣学算法》:重开算法之门,时间复杂度与空间复杂度
Posted 阿迷创客
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了读《趣学算法》:重开算法之门,时间复杂度与空间复杂度相关的知识,希望对你有一定的参考价值。
一、前言
程序 = 数据结构 + 算法
- 时过境迁,自己早已把算法的基础忘记得干干净净,最近看到CSDN发起了《趣学算法》的14天阅读挑战赛,兴趣再次油然而起,既然想学,就不用那么计较,马上就开始!
二、算法复杂度
作为一名从事代码工作的程序员,在设计和优化算法时,首先就会关注到算法的复杂度。算法的复杂度,又分为时间复杂度和空间复杂度。
2.1 复杂度的表示
(1)常数阶: O(1)
- 这应该是程序员追求的复杂度,随着n的增长,复杂度却是常数,例如1,10, 20。通常用 O(1)表示。
(2)多项式阶:O( n n n)、O( n 2 n^2 n2)、O( n 3 n^3 n3)
- 就像我们日常学习的函数多项式,其特点是指数部分为常数,通常用:O( n n n)、O( n 2 n^2 n2)、O( n 3 n^3 n3)来表示,也就是多项式的最高高阶的项。
(3)指数阶:O( 2 n 2^n 2n)、O( n n n^n nn)、O( n ! n! n!)
- 算法效率极差,其复杂度随n呈现指数增长。通常用O( 2 n 2^n 2n)、O( n n n^n nn)、O( n ! n! n!)表示
(4)对数阶:O( log ( n ) \\log(n) log(n))、O( n log ( n ) n\\log(n) nlog(n))
- 算法效率较高,通常用O( log ( n ) \\log(n) log(n))、O( n log ( n ) n\\log(n) nlog(n))表示
算法执行效率, O(1) 最高, 而O(
n
n
n^n
nn) 最低,依次如下:
O(1) > O(
log
(
n
)
\\log(n)
log(n)) > O(
n
n
n) > O(
n
log
(
n
)
n\\log(n)
nlog(n)) > O(
n
2
n^2
n2) > O(
n
3
n^3
n3) > O(
2
n
2^n
2n) > O(
n
!
n!
n!) > O(
n
n
n^n
nn)
2.2 时间复杂度
- 时间复杂度, 即算法运行所需的时间。
例子:实现算法,计算1到n之间所有整数的和,并计算其时间复杂度。
2.2.1 青铜:O( n n n)
int SumFun(int n)
int sum = 0; // 计算 1 次
int i=1; //计算1次
for( ; i<=n; ) //计算n次
sum += i; //计算n次
i++; //计算n次
return sum; //计算1次
即,计算运行时间为:T( n n n) = 1+1+n+n+n+1= 3n+3 ,所以,其算法复杂度可表示为O( n n n)。
2.2.2 王者:O( 1 1 1)
int SumFun(int n)
int sum = 0; // 计算 1 次
sum = (1+n) * n / 2; //加1次赋值,姑且就算4次
return sum; //计算1次
举例:
(1)当n=5时,
1
+
2
+
3
+
4
+
5
⏟
15
\\underbrace1+2+3+4+5_15
15
1+2+3+4+5
(2)当n=6时,
1
+
2
+
3
+
4
+
5
+
6
⏟
21
\\underbrace1+2+3+4+5+6_21
21
1+2+3+4+5+6
即,计算运行时间为:T( n n n) = 1+4+1=6次 ,所以,其算法复杂度可表示为O( 1 1 1)。
备注:计算复杂度时,一般可舍弃不重要的部分,只关心n的最高阶的项
2.3 空间复杂度
空间复杂度, 即算法运行所需的内存空间。
2.3.1 例子:空间复杂度 O( 1 1 1)
int SumFun(int n) //参数入栈,占用空间 1 个 int
int sum = 0; //局部变量,占用空间 1 个 int
int i=1; //局部变量,占用空间 1 个 int
for( ; i<=n; )
sum += i;
i++;
return sum;
即,计算运行时间为:T( n n n) = 1+1+1= 3 ,所以,其算法复杂度可表示为O( 1 1 1)。
2.3.2 例子:空间复杂度 O( n n n)
- 下面以一个递归函数举例
n为正整数,试求n的阶乘,即 f(n) = n! = n*(n-1)*(n-2) … *2 * 1
int fac( int n)
if((n==0) || (n==1))
return 1;
else
return n * fac(n-1);
假设 n=3, 即计算 3! = 3x2x1
- fac(3) = 3 x fac(2) = 3x2xfac(1) = 3x2x1 = 6
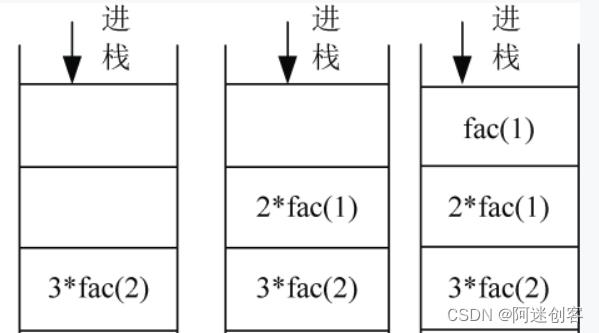
分析:如上图所示,每次递归,都要占用1个栈空间,当n=3时,就占用3个,所以可以估算出其空间复杂度为 O(n)
三、结束语
读完第一章,根据个人理解,做了小小的读书笔记,如有错误,麻烦指正~
四、课后问题
- 谁能帮忙解答一下~
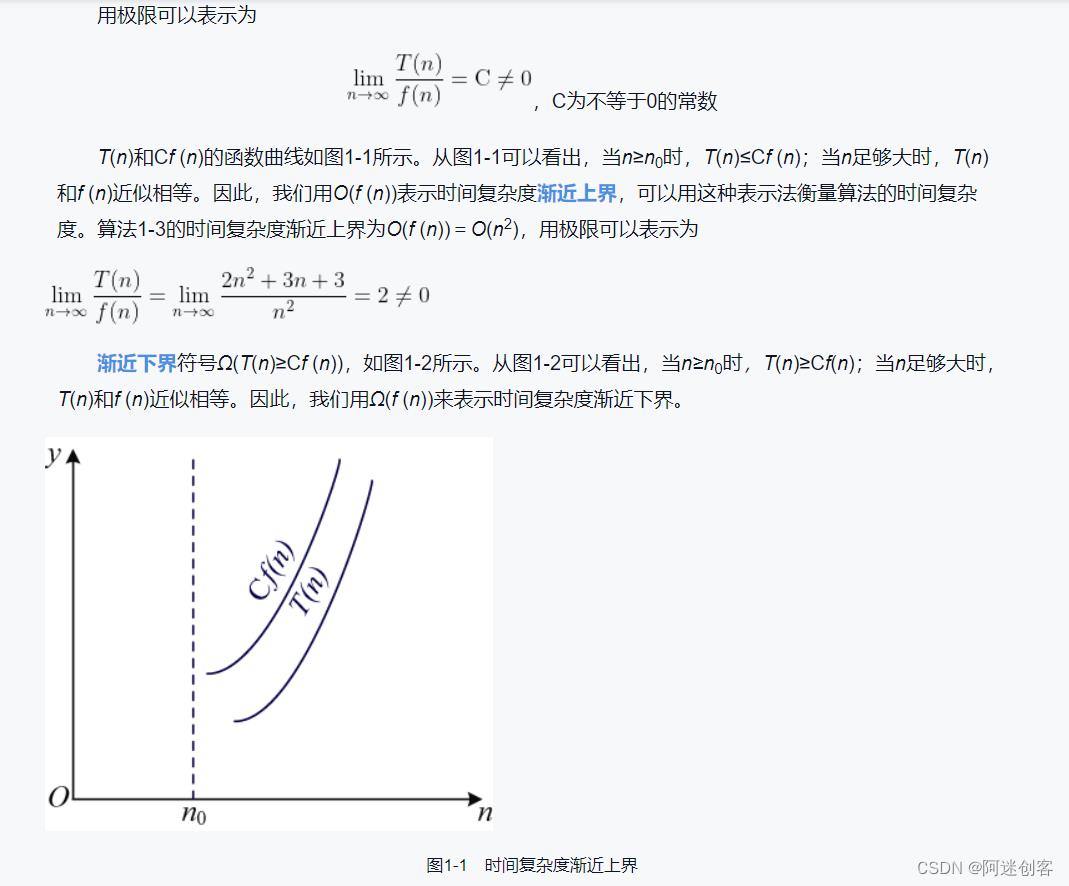
- 请问:1.下图中 f( n n n) 是指 f( n n n)= n 2 n^2 n2吗?Cf( n n n) ==2f( n n n) ?
- 请问:2.下图中的 n 0 n_0 n0是如何计算的? 当T(n) ≤ \\leq ≤Cf(n)时, n 0 n_0 n0是不是该等于 -1?-_-||
以上是关于读《趣学算法》:重开算法之门,时间复杂度与空间复杂度的主要内容,如果未能解决你的问题,请参考以下文章