备战数学建模47-数模常规算法之图论(攻坚站12)

Posted 2022-11-12 nuist__NJUPT

图论〔Graph Theory〕是数学的一个分支。它以图为研究对象。图论中的图是由若干给定的点及连接两点的线所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系，用点代表事物，用连接两点的线表示相应两个事物间具有这种关系。众所周知，图论起源于一个非常经典的问题——柯尼斯堡（Konigsberg）问题。1738年，瑞士数学家欧拉( Leornhard Euler)解决了柯尼斯堡问题。由此图论诞生。欧拉也成为图论的创始人。

注：本篇主要是matlab的工具箱去实现图论的相关算法，没有去讨论太多的理论部分，比如最短路径和最小生成树算法的理论不在此处赘述。

目录

一、图论

1.1、图的基本概念

 1.2、最短路问题及算法

 1.3、MATLAB绘制有向图和无向图

1.4、最小生成树

1.6、 最大流问题

1.7、最小费用最大流问题

---

一、图论

1.1、图的基本概念

由顶点和边组成，就是图，一般图分为无向图和有向图，下面的这个就是无向图，就是无向图就是双向的有向图。当然也有混合图之说，就是既有有向又有无向的。

下面看一下图的一些基本常用如下，了解即可。

我们看一下邻接矩阵的概念，就是将图中的顶点是否连接用0和1表示，1表示连接，0表示未连接。无向图的邻接矩阵是对称的。

 对于有向图的邻接矩阵，都是单向连接的，连通的话就是1，否则就是0.

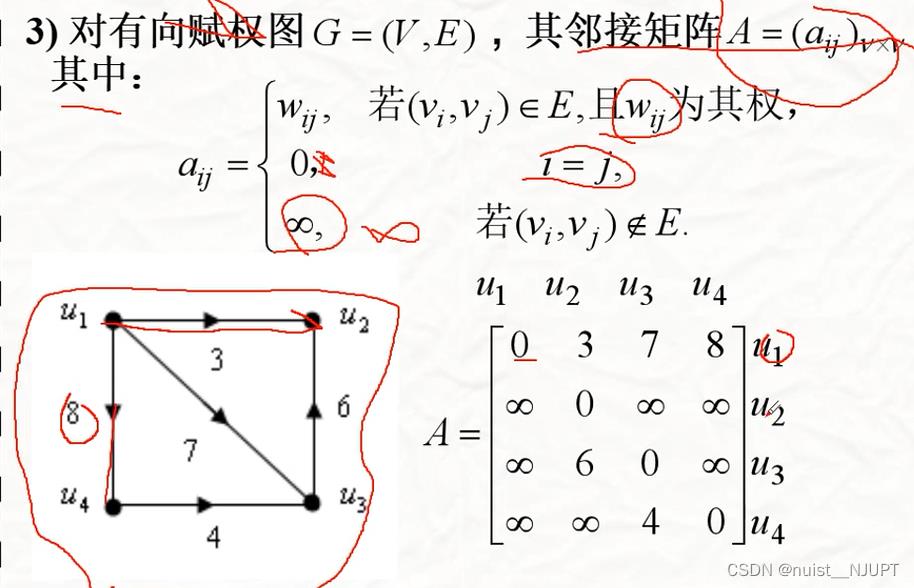
对于带权图的邻接矩阵，顶点之间连通的话，就在邻接矩阵中用相应边的权值表示，顶点不连通的话，就用无穷大表示。

下面看一下无向图的关联矩阵的概念，就是顶点和边直接相连的，我们称之为关联，关联则矩阵中写1，反之，写0.

再看一下有向图的关联矩阵的概念，如果顶点和边直接关联，顶点是头则是-1，顶点是1是尾，否则是0.

我们再看一下顶点中度的概念，对于无向图，与顶点关联的边的数目，就是直接相连的数目称为度。对于无向图而言，有入度和出度的概念，分别是引入顶点和从顶点引出的边的条数。总的度数目=2*总的边数目。

 1.2、最短路问题及算法

我们常用的最短路算法是Dijkstra和Floyd算法，对于单源最短路径使用Dijkstra算法，而对于多源最短路径使用Floyd算法，具体如下：

我们直接看例题吧，这是一个单元最短路问题，即从一个顶点走到另外一个顶点的最小花费。

 我们这里直接使用Matlab自带的求最短路径的函数去求解，代码如下：

clear;
clc
% 编号最好是从1开始连续编号，不要自己随便定义编号,s和t分别是两个顶点
s = [1 1 1 2 3 3 4 5 5  5 5  6  6 7 9 9];
t = [2 3 4 5 2 4 6 4 6  7 8  5  7 8 5 8];
w = [6 3 1 1 2 2 10 6 4 3 6 10  2 4 2 3];
G = digraph(s,t,w);
%绘制有向图
plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2) 
set( gca, 'XTick', [], 'YTick', [] );  
%P是最短路径经过的节点，d是最短距离
[P,d] = shortestpath(G, 1, 8) 

% 在图中高亮我们的最短路径
myplot = plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2);  %首先将图赋给一个变量
highlight(myplot, P, 'EdgeColor', 'r')   %对这个变量即我们刚刚绘制的图形进行高亮处理（给边加上r红色）


% 求出任意两点的最短路径矩阵
D = distances(G)  

% 找出给定范围内的所有点  nearest(G,s,d)
% 返回图形 G 中与节点 s 的距离在 d 之内的所有节点
[nodeIDs,dist] = nearest(G, 1, 8)  

绘制的图形如下，其中红色的部分为最短路径，我们求出最短路径，并在图中用红色标识。

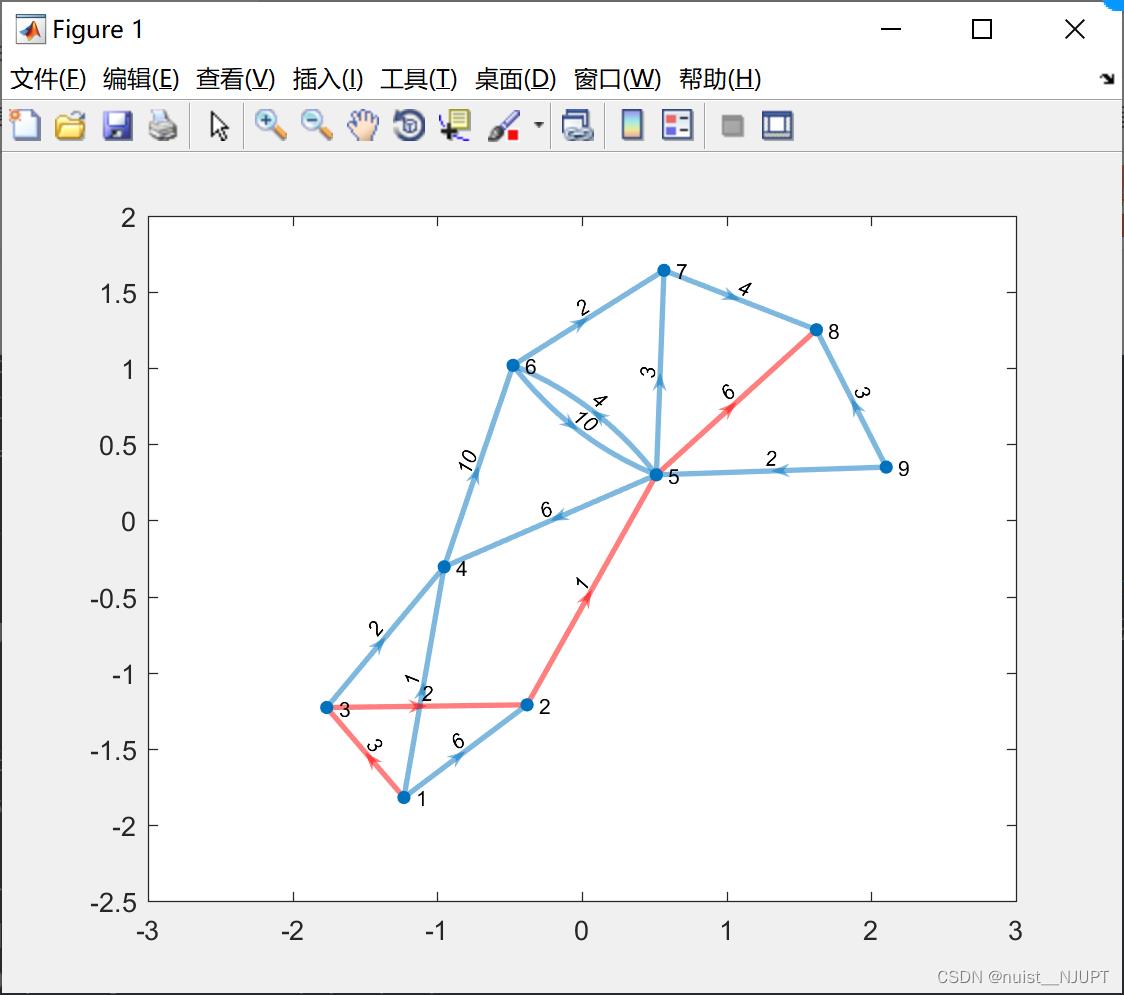
运行的结果如下，其中P表示最短路径，d表示最短路径的长度，D表示任意两点之间的最短路径距离，返回图形 G 中与节点 1 的距离在 8 之内的所有节点。nodeIDs是符合条件的节点，Dist是这些节点与1的距离.

 1.3、MATLAB绘制有向图和无向图

1）无权重的无向图

s1 = [1,2,3,4];
t1 = [2,3,1,1];
G1 = graph(s1, t1);
plot(G1)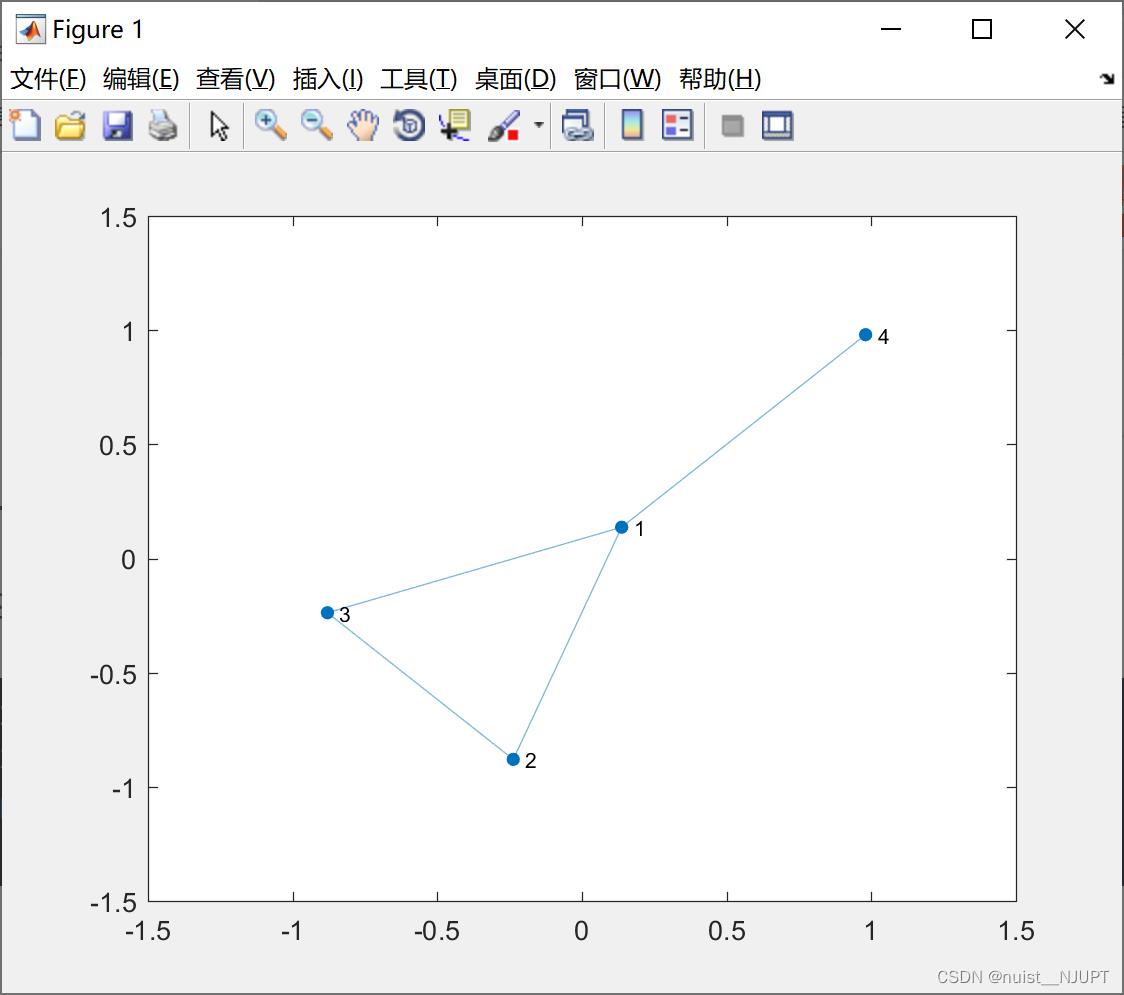

% 注意字符串元胞数组是用大括号包起来的哦
s2 = '学校','电影院','网吧','酒店';
t2 = '电影院','酒店','酒店','KTV';
G2 = graph(s2, t2);
plot(G2, 'linewidth', 2)  % 设置线的宽度
% 下面的命令是在画图后不显示坐标
set( gca, 'XTick', [], 'YTick', [] );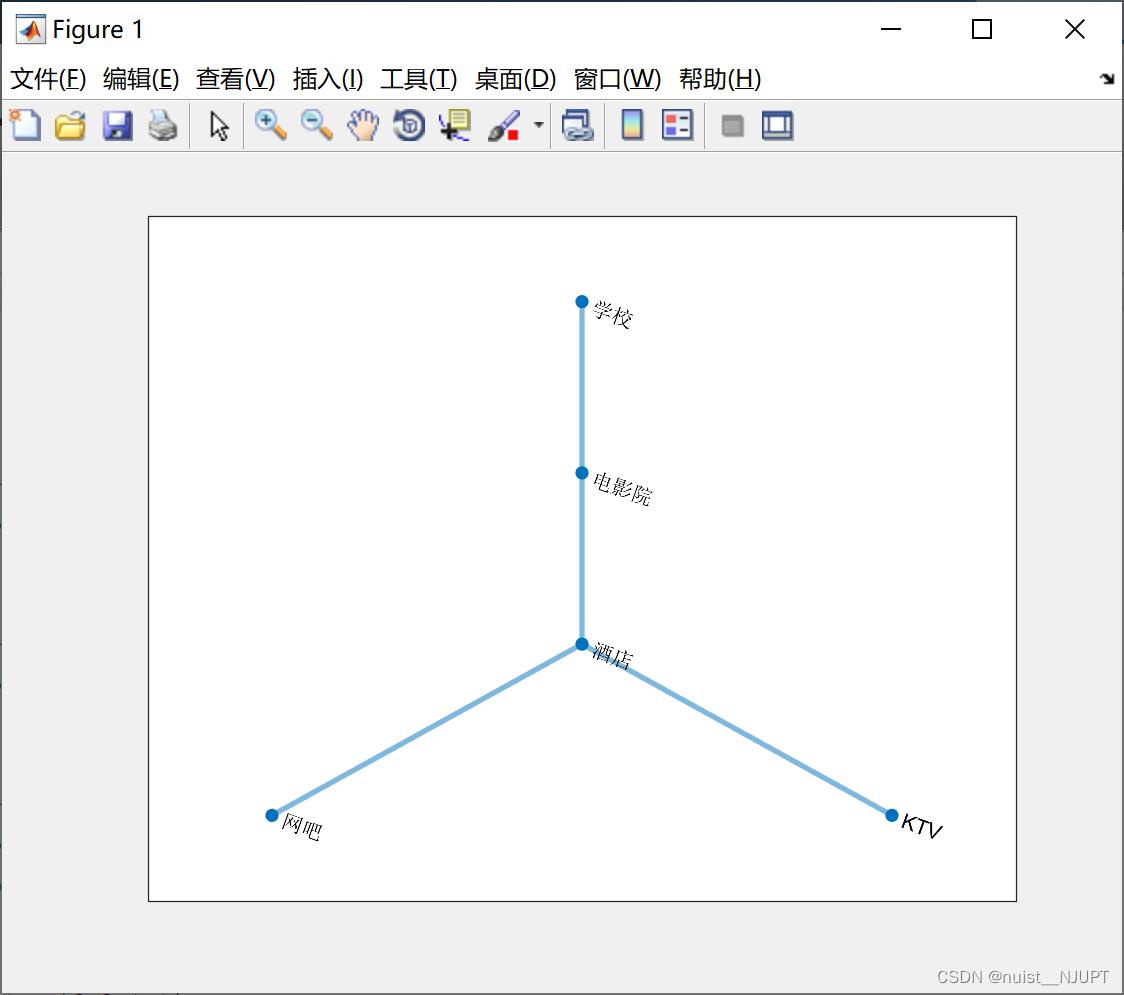  

 

2）有权重的无向图

s = [1,2,3,4];
t = [2,3,1,1];
w = [3,8,9,2];
G = graph(s, t, w)
plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2) 
set( gca, 'XTick', [], 'YTick', [] );  

3）无权重的有向图

% 无权图 digraph(s,t)
s = [1,2,3,4,1];
t = [2,3,1,1,4];
G = digraph(s, t);
plot(G)
set( gca, 'XTick', [], 'YTick', [] );  

4）有权重的有向图

s = [1,2,3,4];
t = [2,3,1,1];
w = [3,8,9,2];
G = digraph(s, t, w);
plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2) 
set( gca, 'XTick', [], 'YTick', [] );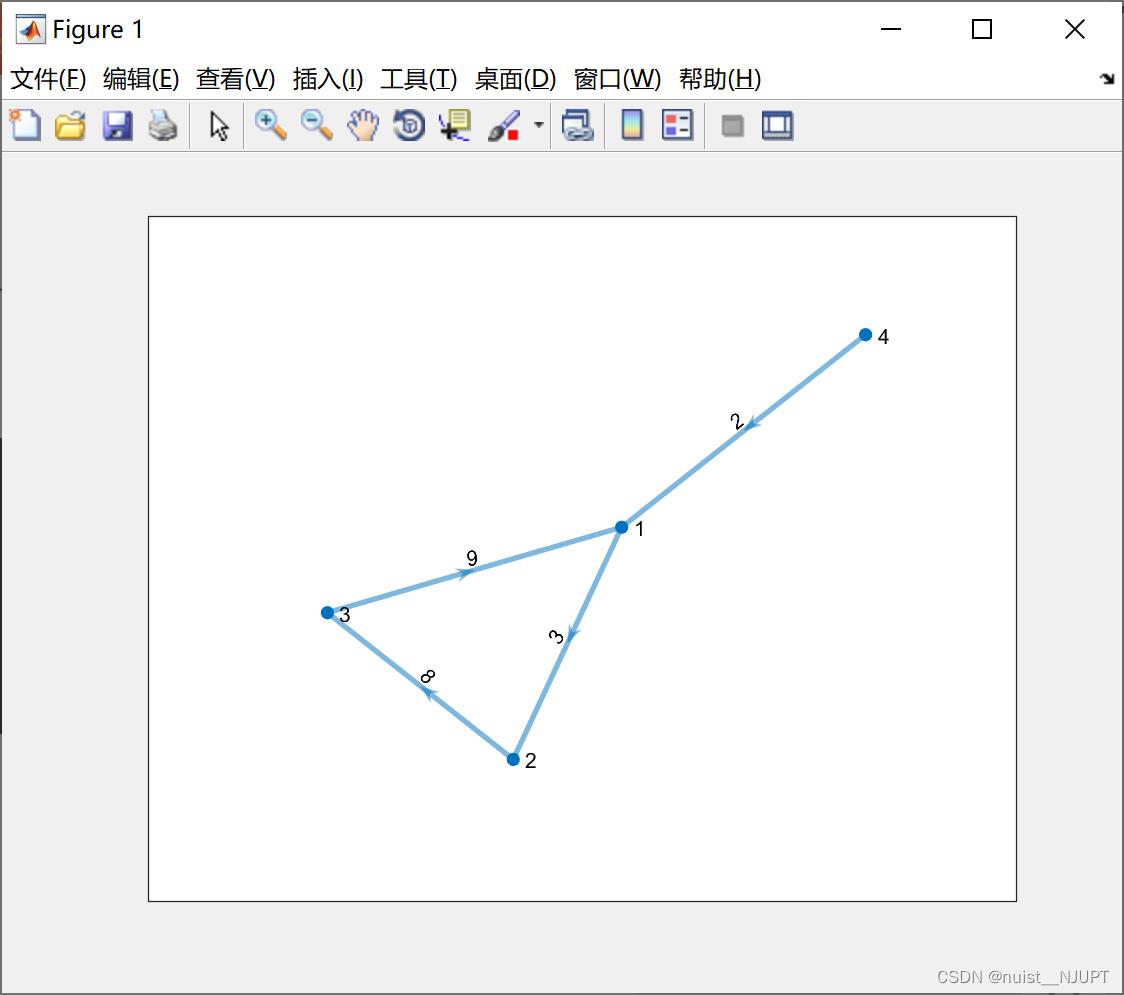  

 

1.4、最小生成树

最小生成树算法主要是cruskal和prime，这里具体的理论不在赘述，需要看理论的自行百度即可，这里演示matlab工具箱实现生成最小生成树。

求下面无向图的最小生产树，如下：

 求图的最小生产树的matlab代码：

clc
clear
a=zeros(11);
a(1,2) =2;a(1,3) =8;a(1,4) =1;
a(2,3) =1 ;a(2,3) =6;a(2,5) =1;
a(3,4) =7 ;a(3,5) =5;a(3,6) =1;
a(3,7 ) =2 ;
a(4,7 ) =9;
a(5,6) =3;a(5,8) =2;a(5,9) =9;
a(5,6) =3;a(5,8) =2;a(5,9) =9;
a(7 ,9) =3;a(7 ,10) =1;
a(8,9) =7;a(8,11) =9;
a(9,10)=1;a(9,11)=2;
a(10,11)=4;

b=sparse(a');
%Tree：给出最后的树的边集答案
%pred：答案中每个边对应的权值
%Kruskal也可以改成Prim
[Tree,pred]=graphminspantree(b,'Method','Kruskal')
view(biograph(Tree,[],'ShowArrows','off'))

绘制的最小生成树图如下所示：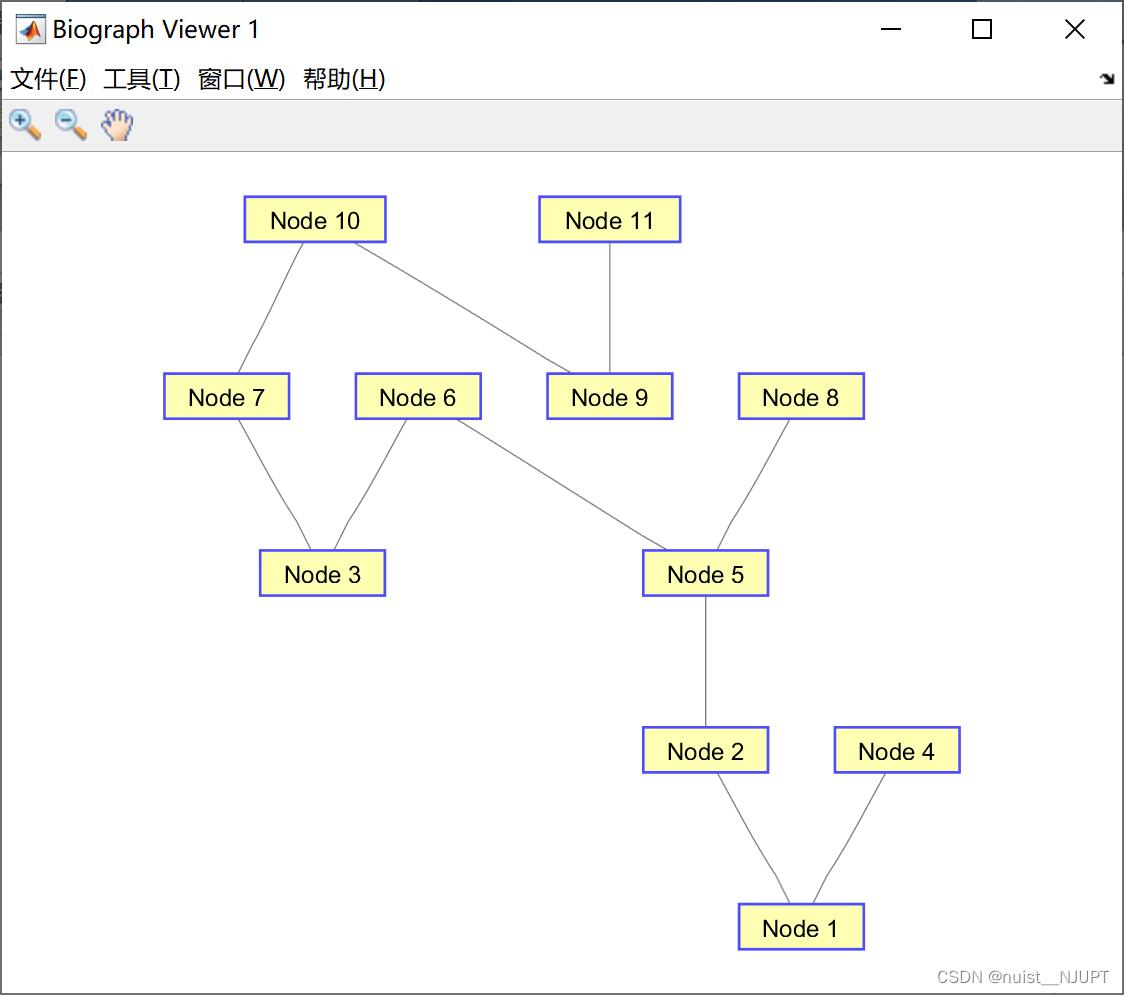

运行的结果如下：

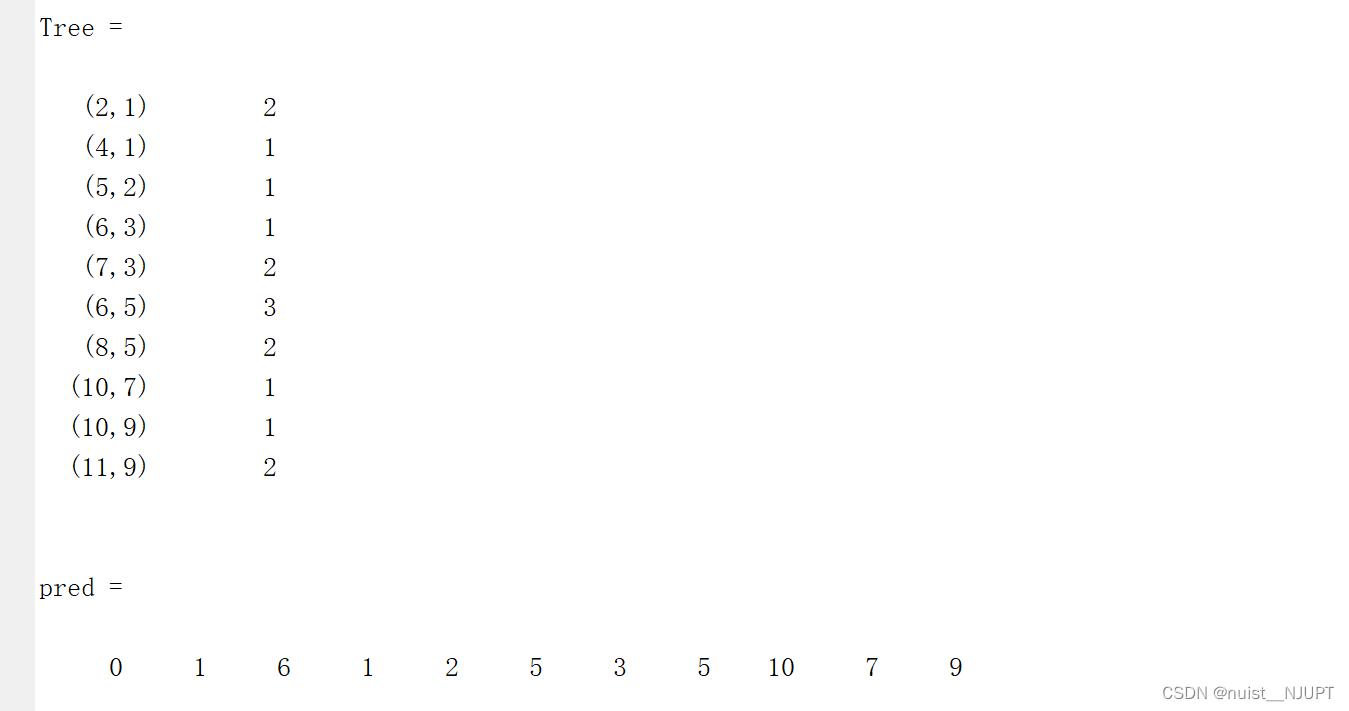
1.6、 最大流问题

比如对于如下的图，我们要使用matlab工具箱求解最大流问题，图中顶点3和4之间有两条弧，删弧（4,3），加入虚拟的顶点9。代码如下：

 我们求出上面有向图的最大费用流，最大费用流为15，代码如下：

clc
clear
a=zeros(9);%创立矩阵
%填写数据
a(1,2)=6; a(1,3)=4; a(1,4)=5;
a(2,3)=3; a(2,5)=9; a(2,6)=9;
a(3,4)=4; a(3,5)=6; a(3,6)=7; a(3,7)=3;
a(4,7)=5; a(4,9)=2;
a(5,8)=12;
a(6,5)=8; a(6,8)=10;
a(7,6)=4; a(7,8)=15;
a(9,3)=2;
b=sparse(a);%通过挤出任何零元素将满矩阵转换为稀疏格式。
[x,y,z]=graphmaxflow(b,1,8)
h = view(biograph(a,[ ],'ShowWeights','on'))%原始容量
view(biograph(y,[],'ShowWeights','on'))  %计算最大流后

原始的图形如下：

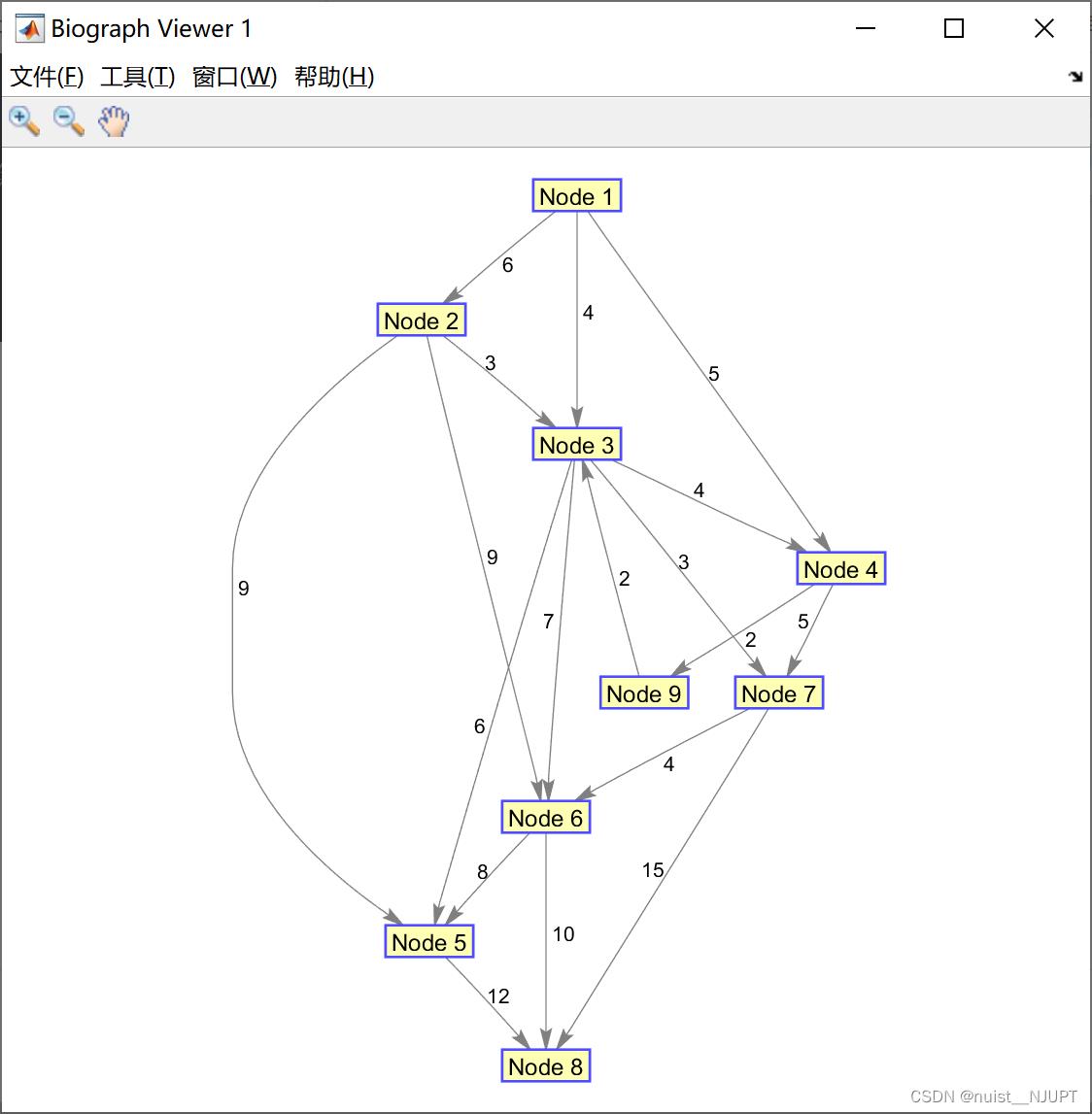
计算最大费用流后绘制的图形如下，显而易见，最大费用流是15，如下：

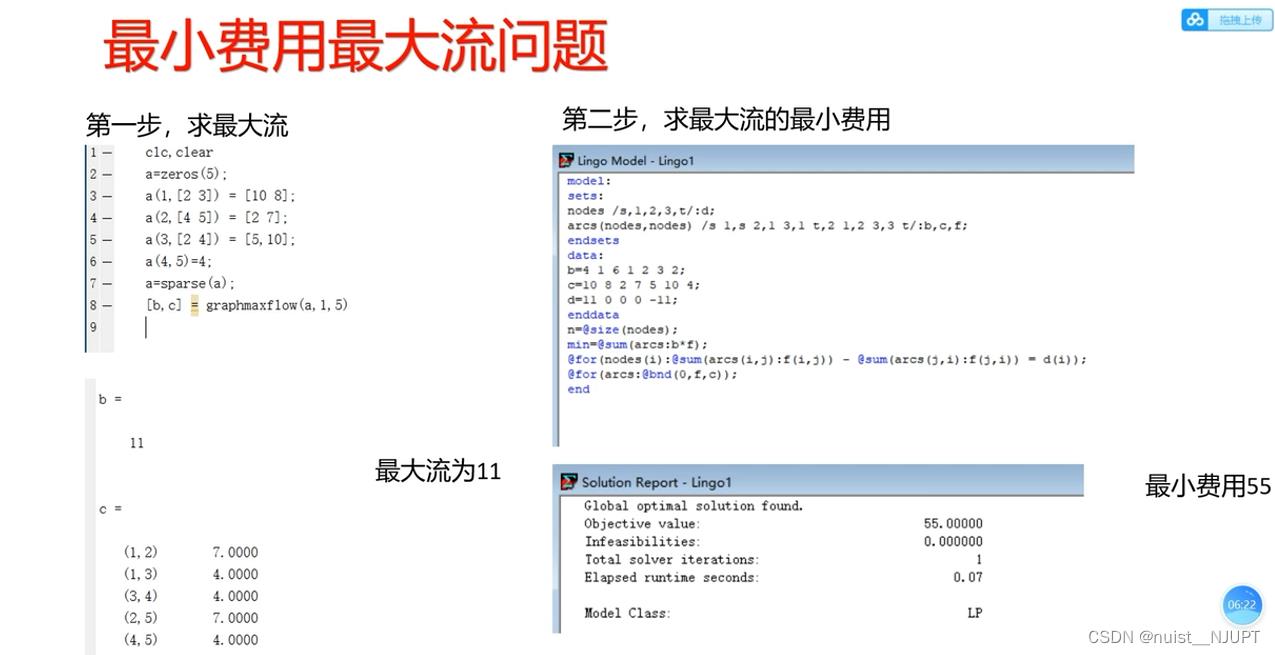
1.7、最小费用最大流问题

我们看下面的最小费用最大流的问题，我们使用matlab求解最大流，然后使用lingo求解最小费用，具体如下：