数学篇08 # 如何利用三角剖分和向量操作描述并处理多边形?
Posted 凯小默
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数学篇08 # 如何利用三角剖分和向量操作描述并处理多边形?相关的知识,希望对你有一定的参考价值。
说明
【跟月影学可视化】学习笔记。
图形学中的多边形是什么?
多边形又可以分为简单多边形和复杂多边形。
- 简单多边形:如果一个多边形的每条边除了相邻的边以外,不和其他边相交。
- 凸多边形:如果一个多边形中的每个内角都不超过 180°。

不同的图形系统如何填充多边形?
1. Canvas2D 如何填充多边形?
Canvas2D 的 fill 还支持两种填充规则:
- nonzero:不管有没有相交的边,只要是由边围起来的区域都一律填充。
- evenodd:根据重叠区域是奇数还是偶数来判断是否填充的
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8" />
<meta http-equiv="X-UA-Compatible" content="IE=edge" />
<meta name="viewport" content="width=device-width, initial-scale=1.0" />
<title>Canvas2D 如何填充多边形</title>
<style>
canvas
border: 1px dashed salmon;
</style>
</head>
<body>
<canvas width="512" height="512"></canvas>
<script type="module">
import Vector2D from "./common/lib/vector2d.js";
const canvas = document.querySelector("canvas");
const ctx = canvas.getContext("2d");
const width, height = canvas;
const w = 0.5 * width,
h = 0.5 * height;
ctx.translate(w, h);
ctx.scale(1, -1);
// 绘制坐标轴
function drawAxis()
ctx.save();
ctx.strokeStyle = "#ccc";
ctx.beginPath();
ctx.moveTo(-w, 0);
ctx.lineTo(w, 0);
ctx.stroke();
ctx.beginPath();
ctx.moveTo(0, -h);
ctx.lineTo(0, h);
ctx.stroke();
ctx.restore();
drawAxis();
// nonzero:不管有没有相交的边,只要是由边围起来的区域都一律填充。
// evenodd:根据重叠区域是奇数还是偶数来判断是否填充的
function draw(
context,
points,
fillStyle = "salmon", close = false, rule = "nonzero" =
)
context.beginPath();
context.moveTo(...points[0]);
for (let i = 1; i < points.length; i++)
context.lineTo(...points[i]);
if (close) context.closePath();
context.fillStyle = fillStyle;
context.fill(rule);
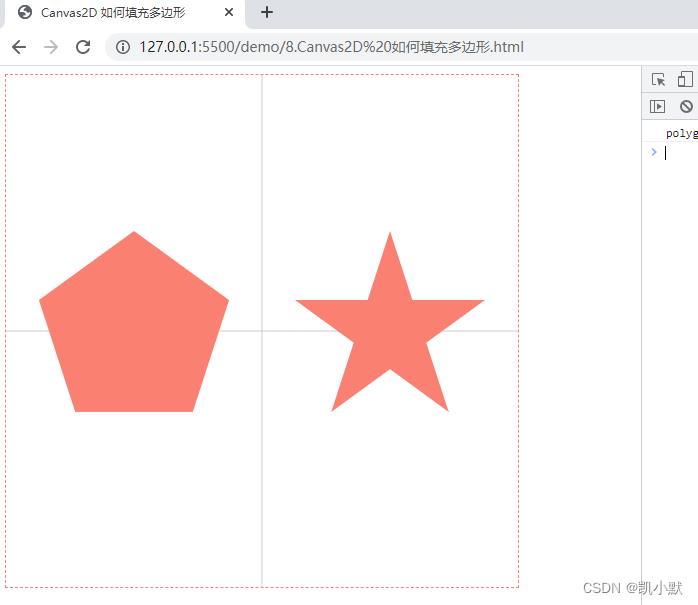
// 构建多边形的顶点,这里来5个
const points = [new Vector2D(0, 100)];
for (let i = 1; i <= 4; i++)
const p = points[0].copy().rotate(i * Math.PI * 0.4);
points.push(p);
// 绘制正五边形
const polygon = [...points]; // polygon 数组是正五边形的顶点数组
ctx.save();
ctx.translate(-128, 0);
draw(ctx, polygon);
ctx.restore();
console.log("polygon--->", polygon);
// 绘制正五角星
const stars = [
points[0],
points[2],
points[4],
points[1],
points[3],
]; // stars 数组是把正五边形的顶点顺序交换之后,构成的五角星的顶点数组。
ctx.save();
ctx.translate(128, 0);
draw(ctx, stars);
// draw(ctx, stars, rule: 'evenodd');
ctx.restore();
</script>
</body>
</html>
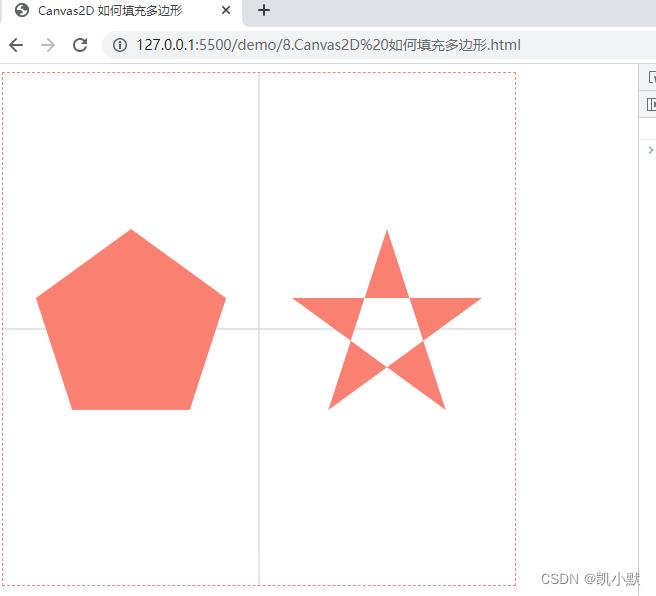
如果改成 rule: 'evenodd' 绘制五角星
draw(ctx, stars, rule: 'evenodd');
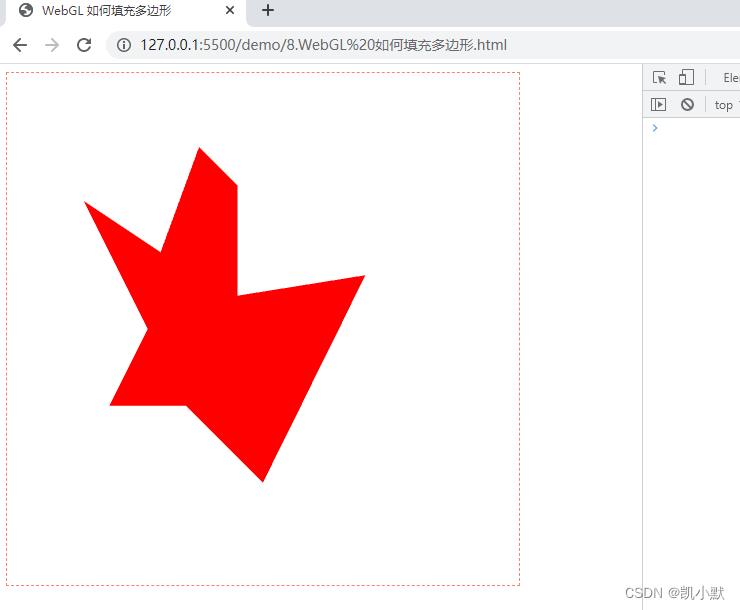
2. WebGL 如何填充多边形?
将多边形分割成若干个三角形的操作,在图形学中叫做三角剖分(Triangulation)。对 3D 模型,WebGL 在绘制的时候,也需要使用三角剖分,而 3D 的三角剖分又被称为网格化(Meshing)。
推荐学习:Delaunay Triangulation In Two and Three Dimensions
可以使用下面库来对多边形进行三角剖分:
以最简单的 Earcut 库(代码:https://github.com/mapbox/earcut/blob/master/src/earcut.js)为例,来了解 WebGL 填充多边形的过程
以下面这个多边形为例子,我们利用 Earcut 库对其进行三角剖分

<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8" />
<meta http-equiv="X-UA-Compatible" content="IE=edge" />
<meta name="viewport" content="width=device-width, initial-scale=1.0" />
<title>WebGL 如何填充多边形</title>
<style>
canvas
border: 1px dashed salmon;
</style>
</head>
<body>
<canvas width="512" height="512"></canvas>
<script type="module">
const canvas = document.querySelector("canvas");
const gl = canvas.getContext("webgl");
const vertex = `
attribute vec2 position;
void main()
gl_PointSize = 1.0;
gl_Position = vec4(position, 1.0, 1.0);
`;
const fragment = `
precision mediump float;
void main()
gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);
`;
const vertexShader = gl.createShader(gl.VERTEX_SHADER);
gl.shaderSource(vertexShader, vertex);
gl.compileShader(vertexShader);
const fragmentShader = gl.createShader(gl.FRAGMENT_SHADER);
gl.shaderSource(fragmentShader, fragment);
gl.compileShader(fragmentShader);
const program = gl.createProgram();
gl.attachShader(program, vertexShader);
gl.attachShader(program, fragmentShader);
gl.linkProgram(program);
gl.useProgram(program);
// 不规则多边形的顶点
const vertices = [
[-0.7, 0.5],
[-0.4, 0.3],
[-0.25, 0.71],
[-0.1, 0.56],
[-0.1, 0.13],
[0.4, 0.21],
[0, -0.6],
[-0.3, -0.3],
[-0.6, -0.3],
[-0.45, 0.0],
];
// 使用 Earcut 库进行三角剖分:Earcut 库只接受扁平化的定点数据
import earcut from "./common/lib/earcut.js";
// 使用数组的 flat 方法将顶点扁平化
const points = vertices.flat();
// 进行三角剖分
const triangles = earcut(points);
const position = new Float32Array(points);
const cells = new Uint16Array(triangles);
const pointBuffer = gl.createBuffer();
gl.bindBuffer(gl.ARRAY_BUFFER, pointBuffer);
gl.bufferData(gl.ARRAY_BUFFER, position, gl.STATIC_DRAW);
const vPosition = gl.getAttribLocation(program, "position");
gl.vertexAttribPointer(vPosition, 2, gl.FLOAT, false, 0, 0);
gl.enableVertexAttribArray(vPosition);
const cellsBuffer = gl.createBuffer();
gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, cellsBuffer);
gl.bufferData(gl.ELEMENT_ARRAY_BUFFER, cells, gl.STATIC_DRAW);
gl.clear(gl.COLOR_BUFFER_BIT);
gl.drawElements(gl.TRIANGLES, cells.length, gl.UNSIGNED_SHORT, 0);
// 用描边 LINE_STRIP 代替填充 TRIANGLES
// gl.drawElements(gl.LINE_STRIP, cells.length, gl.UNSIGNED_SHORT, 0);
</script>
</body>
</html>
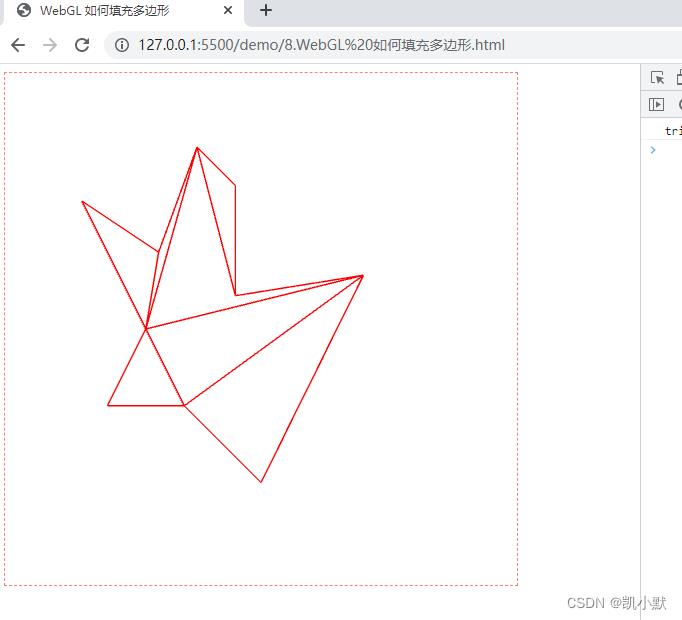
可以通过用描边 LINE_STRIP 代替填充 TRIANGLES 就可以清晰的看到这个多边形被分割成了多个三角形
// 用描边LINE_STRIP 代替填充 TRIANGLES
gl.drawElements(gl.LINE_STRIP, cells.length, gl.UNSIGNED_SHORT, 0);
注意:三角剖分后返回的数组里的值是顶点数据的 index。

如何判断点在多边形内部?
判断一个点是否在多边形内部时,需要先对多边形进行三角剖分,然后判断该点是否在其中一个三角形内部。
1. Canvas2D 如何判断点在多边形内部?
我们先使用 canvas2d 绘制出来上面的多边形
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8" />
<meta http-equiv="X-UA-Compatible" content="IE=edge" />
<meta name="viewport" content="width=device-width, initial-scale=1.0" />
<title>Canvas2D 如何判断点在多边形内部</title>
<style>
canvas
border: 1px dashed salmon;
</style>
</head>
<body>
<canvas width="512" height="512"></canvas>
<script type="module">
const vertices = [
[-0.7, 0.5],
[-0.4, 0.3],
[-0.25, 0.71],
[-0.1, 0.56],
[-0.1, 0.13],
[0.4, 0.21],
[0, -0.6],
[-0.3, -0.3],
[-0.6, -0.3],
[-0.45, 0.0],
];
const canvas = document.querySelector("canvas");
const ctx = canvas.getContext("2d");
const width, height = canvas;
ctx.translate(0.5 * width, 0.5 * height);
ctx.scale(1, -1);
const poitions = vertices.map(([x, y]) => [x * 256, y * 256]);
function draw(
ctx,
points,
strokeStyle = "salmon",
fillStyle = null
)
ctx.strokeStyle = strokeStyle;
ctx.beginPath();
ctx.moveTo(...points[0]);
for (let i = 1; i < points.length; i++)
ctx.lineTo(...points[i]);
ctx.closePath();
if (fillStyle)
ctx.fillStyle = fillStyle;
ctx.fill();
ctx.stroke();
draw(ctx, poitions, "transparent", "salmon");
// draw(ctx, [[100, 100], [100, 200], [150, 200]], 'transparent', 'salmon');
const left, top = canvas.getBoundingClientRect();
canvas.addEventListener("mousemove", (evt) =>
const x, y = evt;
// 坐标转换
const offsetX = x - left;
const offsetY = y - top;
ctx.clearRect(-256, -256, 512, 512);
if (ctx.isPointInPath(offsetX, offsetY))
draw(ctx, poitions, "transparent", "green");
// draw(ctx, [[100, 100], [100, 200], [150, 200]], 'transparent', 'green');
else
draw(ctx, poitions, "transparent", "salmon");
// draw(ctx, [[100, 100], [100, 200], [150, 200]], 'transparent', 'salm以上是关于数学篇08 # 如何利用三角剖分和向量操作描述并处理多边形?的主要内容,如果未能解决你的问题,请参考以下文章