youcans 的图像处理学习课11. 形态学图像处理（中）

Posted YouCans

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了youcans 的图像处理学习课11. 形态学图像处理（中）相关的知识，希望对你有一定的参考价值。

专栏地址：『youcans 的图像处理学习课』
文章目录：『youcans 的图像处理学习课 - 总目录』


【youcans 的 OpenCV 学习课】11. 形态学图像处理（中）

文章目录

3. 形态学算法

形态学处理的主要应用是提取图像中用来表示和描述形状的元素和成分，例如提取边界、连通分量、凸壳和区域骨架。


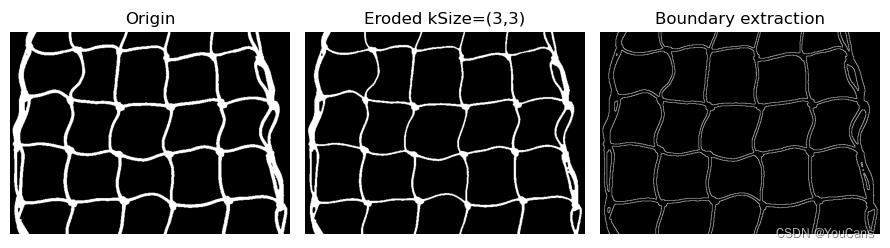
3.1 边界提取

边界提取的原理是通过对目标图像进行腐蚀和膨胀处理，比较结果图像与原图像的差别来实现。

内边界的提取可以利用图像的腐蚀处理得到原图像的一个收缩，再将收缩结果与目标图像进行异或运算，实现差值部分的提取。

集合 A 的边界 β ( A ) \\beta (A) β(A) 可以通过合适的结构元 B 腐蚀集合 A，然后求 A 与腐蚀结果的差集来实现：
β ( A ) = A − ( A ⊖ B ) \\beta(A) = A -(A \\ominus B) β(A)=A−(A⊖B)

常用的结构元 B 是 3*3 的全 1 核，而 5*5 的全 1 核往往可以得到2～3个像素宽度的边界。

类似地，外边界提取先对图像进行膨胀处理，然后用膨胀结果与原目标图像进行异或运算，也就是求膨胀结果与原目标图像的差集。


例程 10.10：形态算法之边界提取

    # 10.10 形态算法之边界提取
    imgGray = cv2.imread("../images/imgNetrope.png", flags=0)  # flags=0 读取为灰度图像
    ret, imgBin = cv2.threshold(imgGray, 25, 255, cv2.THRESH_BINARY_INV | cv2.THRESH_OTSU)  # 二值化处理

    kSize = (3, 3)  # 卷积核的尺寸
    kernel = np.ones(kSize, dtype=np.uint8)  # 生成盒式卷积核
    imgErode1 = cv2.erode(imgBin, kernel=kernel)  # 图像腐蚀
    imgBound1 = imgBin - imgErode1  # 图像边界提取

    plt.figure(figsize=(9, 5))
    plt.subplot(131), plt.axis('off'), plt.title("Origin")
    plt.imshow(imgBin, cmap='gray', vmin=0, vmax=255)
    plt.subplot(132), plt.title("Eroded kSize=(3,3)"), plt.axis('off')
    plt.imshow(imgErode1, cmap='gray', vmin=0, vmax=255)
    plt.subplot(133), plt.title("Boundary extraction"), plt.axis('off')
    plt.imshow(imgBound1, cmap='gray', vmin=0, vmax=255)
    plt.tight_layout()
    plt.show()


3.2 孔洞填充

孔洞是被前景像素连成的边框包围的背景区域。书法作品图像中存在孔洞，在图像分割后也经常会有一些孔洞。

闭运算孔洞填充：

形态学闭运算可以用来实现孔洞填充，闭运算先膨胀后腐蚀操作，膨胀使白色高亮区域增加，孔洞会被填充，但需要准确设置核大小，因此不是通用的方法。

约束膨胀孔洞填充：

冈萨雷斯《数字图像处理（第四版）》提供了一种孔洞填充的形态学算法，构造一个元素为 0 的阵列 X 0 X_0 X0​，其中对应孔洞的像素值为 1，采用迭代过程可以填充所有的孔洞：
X k = ( X k − 1 ⊕ B ) ∩ I c ,   k = 1 , 2 , 3... X_k = (X_k-1 \\oplus B) \\cap I^c, \\ k=1,2,3... Xk​=(Xk−1​⊕B)∩Ic, k=1,2,3...

先找到孔洞中的一个点，用结构元进行膨胀，然后用原始图像的补集进行约束（交集运算），不断迭代重复这一操作直到算法收敛，就得到孔洞填充图。

泛洪算法孔洞填充：

OpenCV 中提供了一种孔洞填充方法“泛洪填充法”，也成为“漫水填充法“。其原理是将像素点的灰度值视为高度，整个图像就像一张高低起伏的地形图，向洼地注水将会淹没低洼区域，从而实现孔洞填充。

漫水填充经常被用来标记或分离图像的一部分以便对其进行进一步处理或分析，也可以用来从输入图像获取掩码区域，掩码会加速处理过程，或只处理掩码指定的像素点，操作的结果总是某个连续的区域。

OpenCV 中的函数 cv.floodFill 可以实现漫水填充方法 。

函数说明：

cv.floodFill(image, mask, seedPoint, newVal[, loDiff[, upDiff[, flags]]]) -> retval, image, mask, rect

参数说明：

  • image：输入图像，可以为单通道或多通道，图像深度必须为8bit 或浮点类型。
  • dst：输出图像，大小和类型与 src 相同
  • mask：掩模图像，必须为单通道、8bit，且比 image 宽 2个像素、高 2个像素
  • setPoint：起始像素点
  • newVal：重绘像素区域的新的填充值（颜色）
  • rect：可选项，返回重绘区域的最小绑定矩形
  • loDiff：可选项，当前选定像素与其连通区中相邻像素中的一个像素，或者与加入该连通区的一个 seedPoint像素，二者之间的最大下行差异值。
  • upDiff：可选项，当前选定像素与其连通区中相邻像素中的一个像素，或者与加入该连通区的一个 seedPoint像素，二者之间的最大上行差异值。
  • flags：标志位，可选项，32bit 整型数据，由3部分组成： 0-7bit 表示邻接性（4邻接、8邻接）；8-15bit 表示 mask 的填充颜色；16-31bit 表示填充模式：
    • cv.FLOODFILL_FIXED_RANGE：如果设置则考虑当前像素和种子像素之间的差异，否则将考虑相邻像素之间的差异
    • cv.FLOODFILL_MASK_ONLY：如果设置则不改变原始图像，并忽略 newVal，只使用上述标志位 8-16 中指定的值填充掩码。本选项仅在具有掩模图像时适用。

注意事项：

  • 原始图像 image 仅当 flags 设置为 FLOODFILL_MASK_ONLY 时不会被修改，否则原始图像会被修改。
  • 由于掩模比原始图像大，所以图像中的像素 (x,y) 对应于掩模中的像素 (x+1,y+1)。
  • Flood-filling 不能跨越掩模图像中的非 0 像素，因此边缘检测的结果可以作为mask来阻止边缘填充。
  • 泛洪填充法可以用特定的颜色填充联通区域（newVal），参见例程 10.10。

例程 10.11：约束膨胀算法实现孔洞填充

    # 10.11 约束膨胀算法实现孔洞填充
    # 本算法参考：冈萨雷斯《数字图像处理（第四版）》 9.5.2 孔洞填充
    # 图像为二值化图像，255 白色为目标物，0 黑色为背景，要填充白色目标物中的黑色空洞
    imgGray = cv2.imread("../images/imgBloodCell.png", flags=0)  # flags=0 读取为灰度图像
    ret, imgBin = cv2.threshold(imgGray, 127, 255, cv2.THRESH_BINARY_INV | cv2.THRESH_OTSU)  # 二值化处理
    imgBinInv = cv2.bitwise_not(imgBin)  # 二值图像的补集

    kernel = cv2.getStructuringElement(cv2.MORPH_ELLIPSE, (3, 3))  # 构造 3×3 十字形结构元
    F = np.zeros(imgBin.shape, np.uint8)  # 构建阵列 F，并写入 BinInv 的边界值
    F[:, 0] = imgBinInv[:, 0]
    F[:, -1] = imgBinInv[:, -1]
    F[0, :] = imgBinInv[0, :]
    F[-1, :] = imgBinInv[-1, :]

    # 循环迭代：对 F 进行膨胀，膨胀结果与 BinInv 进行 AND 操作
    Flast = F.copy()
    for i in range(1000):
        F_dilation = cv2.dilate(F, kernel)
        F = cv2.bitwise_and(F_dilation, imgBinInv)
        if (F==Flast).all():
            break  # 结束迭代算法
        else:
            Flast = F.copy()
        if i==100: imgF100 = F  # 中间结果

    print("iter =".format(i))  # 迭代次数
    plt.figure(figsize=(9, 5))
    plt.subplot(131), plt.axis('off'), plt.title("Origin")
    plt.imshow(imgGray, cmap='gray', vmin=0, vmax=255)
    plt.subplot(132), plt.title("Hole filled (iter=100)"), plt.axis('off')
    plt.imshow(imgF100, cmap='gray', vmin=0, vmax=255)
    plt.subplot(133), plt.title("Hole filled (iter=)".format(i)), plt.axis('off')
    plt.imshow(F, cmap='gray', vmin=0, vmax=255)
    plt.tight_layout()
    plt.show()


例程 10.12：泛洪算法实现孔洞填充

    # 10.12 泛洪算法实现孔洞填充 (cv2.floodFill)
    # 图像为二值化图像，255 白色为目标物，0 黑色为背景，要填充白色目标物中的黑色空洞
    imgGray = cv2.imread("../images/imgBloodCell.png", flags=0)  # flags=0 读取为灰度图像
    ret, imgBin = cv2.threshold(imgGray, 127, 255, cv2.THRESH_BINARY_INV | cv2.THRESH_OTSU)  # 二值化处理

    h, w = imgBin.shape[:2]
    mask = np.zeros((h+2, w+2), np.uint8)  # 掩模图像比原始图像宽 2 个像素、高 2 个像素

    imgFloodfill = imgBin.copy()
    # isbreak = False
    # for i in range(imgFloodfill.shape[0]):
    #     for j in range(imgFloodfill.shape[1]):
    #         if (imgFloodfill[i][j] == 0):  # seedPoint对应像素必须是背景
    #             seedPoint = (i, j)
    #             isbreak = True
    #             break
    #     if (isbreak):
    #         break
    # cv2.floodFill(imgFloodfill, mask, seedPoint, 255)  # 从 seedPoint 开始，必须是背景像素
    cv2.floodFill(imgFloodfill, mask, (0, 0), newVal=225)  # 算法从背景像素原点 (0, 0) 开始
    imgFloodfillInv = cv2.bitwise_not(imgFloodfill)  # 计算补集
    imgHoleFilled = imgBin | imgFloodfillInv  # 计算交集
    imgRebuild = cv2.bitwise_not(imgHoleFilled)  # 计算补集

    plt.figure(figsize=(9, 5))
    plt.subplot(131), plt.axis('off'), plt.title("Origin")
    plt.imshow(imgGray, cmap='gray', vmin=0, vmax=255)
    plt.subplot(132), plt.title("Flood filled"), plt.axis('off')
    plt.imshow(imgFloodfill, cmap='gray', vmin=0, vmax=255)
    plt.subplot(133), plt.title("Hole filled image"), plt.axis('off')
    plt.imshow(imgRebuild, cmap='gray', vmin=0, vmax=255)
    plt.tight_layout()
    plt.show()


3.3 提取连通分量

从二值图像中提取连通分量是自动图像分析的核心步骤。

约束膨胀提取连通分量：

冈萨雷斯《数字图像处理（第四版）》提供了一种提取连通分量的形态学算法，构造一个元素为 0 的阵列 X 0 X_0 X0​，其中对应连通分量的像素值为 1，采用迭代过程可以得到所有的连通分量：
X k = ( X k − 1 ⊕ B ) ∩ I ,   k = 1 , 2 , 3... X_k = (X_k-1 \\oplus B) \\cap I, \\ k=1,2,3... Xk​=(Xk−1​⊕B)∩I, k=1,2,3...

该算法与约束膨胀孔洞填充的思路相同，使用条件膨胀来限制膨胀的增长，但用 I I I 代替 I c I^c Ic 以寻找前景点。

对于内含多个连通分量的图像 A，从仅为连通分量 A1 内部的某个像素 B 开始，用 3*3的结构元不断进行膨胀。由于其它连通分量与 A1 之间至少有一条像素宽度的空隙，每次膨胀都不会产生位于其它连通区域内的点。用每次膨胀后的图像与原始图像 A 取交集，就把膨胀限制在 A1 内部。随着集合 B 的不断膨胀，B 的区域不断生长，但又被限制在连通分量 A1 的内部，最终就会充满整个连通分量 A1，从而实现对连通分量 A1 的提取。

提取连通分量的过程也是对连通分量的标注，通常给图像中的每个连通区分配编号，在输出图像中该连通区内的所有的像素值赋值为对应的区域编号，这样的输出图像被称为标注图像。


例程 10.13：形态算法之提取连通分量

    # # 10.13 约束膨胀算法提取连通分量
    # 本算法参考：冈萨雷斯《数字图像处理（第四版）》 9.5.3 提取连通分量
    # 图像为二值化图像，255 白色为目标物，0 黑色为背景
    imgGray = cv2.imread("../images/Fig0918a.tif", flags=0)  # flags=0 读取为灰度图像
    # 预处理
    ret, imgThresh = cv2.threshold(imgGray, 200, 255, cv2.THRESH_BINARY_INV)  # 二值化处理
    kernel = np.ones((3, 3), dtype=np.uint8)  # 生成盒式卷积核
    imgClose = cv2.morphologyEx(imgThresh, cv2.MORPH_CLOSE, kernel)  # 闭运算，消除噪点
    imgErode = cv2.erode(imgClose, kernel=kernel)  # 腐蚀运算，腐蚀亮点

    imgBin = imgErode
    imgBinCopy = imgBin.copy()  # 复制 imgBin
    xBinary = np.zeros(imgBin.shape, np.uint8)  # 大小与 img 相同，像素值为 0
    kernel = cv2.getStructuringElement(cv2.MORPH_ELLIPSE, (3, 3))  # 3×3结构元
    count = []  # 为了记录连通分量中的像素个数
    while imgBinCopy.any():  # 循环迭代，直到 imgBinCopy 中的像素值全部为0
        Xa_copy, Ya_copy = np.where(imgBinCopy > 0)  # imgBinCopy 中值为255的像素的坐标
        xBinary[Xa_copy[0]][Ya_copy[0]] = 255  # 选取第一个点，并将 xBinary 中对应像素值改为255

        # 约束膨胀，先对 xBinary 膨胀，再与 imgBin 执行与操作（取交集）
        for i in range(100):
            dilation_B = cv2.dilate(xBinary, kernel)
            xBinary = cv2.bitwise_and(imgBin, dilation_B)

        # 取 xBinary 值为255的像素坐标，并将 imgBinCopy 中对应坐标像素值变为0
        Xb, Yb = np.where(xBinary > 0)
        imgBinCopy[Xb, Yb] = 0

        # 显示连通分量及其包含像素数量
        count.append(len(Xb))
        lenCount = len(count)
        if lenCount == 0:
            print("无连通分量")
        elif lenCount == 1:
            print("第1个连通分量为".format(count[0]))
        else:
            print("第个连通分量为".format(len(count), count[-1]-count[-2]))

    # print(count)
    plt.figure(figsize=(12, 6))
    plt.subplot(231), plt.axis('off'), plt.title("origin")
    plt.imshow(imgGray, cmap='gray', vmin=0, vmax=255)
    plt.subplot(232), plt.title("threshold"), plt.axis('off')
    plt.imshow(imgBin, cmap='gray', vmin=0, vmax=255)
    plt.subplot(233), plt.title("closed image"), plt.axis('off')
    plt.imshow(imgClose, cmap='gray', vmin=0, vmax=255)
    plt.subplot(234), plt.title("eroded image"), plt.axis('off')
    plt.imshow(imgErode, cmap='gray', vmin=0, vmax=255)
    plt.subplot(235), plt.title("xBinary"youcans 的图像处理学习课11. 形态学图像处理（中）


 youcans 的图像处理学习课11. 形态学图像处理（上）


 youcans 的图像处理学习课11. 形态学图像处理（下）


 youcans 的图像处理学习课11. 形态学图像处理（下）


 youcans 的图像处理学习课11. 形态学图像处理（上）


 youcans 的图像处理学习课11. 形态学图像处理（中）