深度学习基础之正向传播与反向传播

Posted 2022-10-03 Icy Hunter

文章目录

• 前言
• 正向传播
• 链式法则
• 反向传播
• • 加法节点的反向传播
  • 乘法节点的反向传播
  • 小结
• 实例
• • Sigmoid函数
  • Softmax-with-Loss 层
• 参考

前言

因为这学期上了一门深度学习的课，老师上课推公式，写密密麻麻一黑板，看也看不清，讲完擦了之后说这推导如果考试必考，人都傻了，只能回过头来看她课件理解理解了。
以下都是以计算图为例。

正向传播

正向传播非常好理解，就是一步一步算到最后。

这是一个基于计算图求解出最后结果的一个例子。
一步步从左向右计算，最后得出结果，这就是称为正向传播（forward propagation）。

使用计算图的好处：局部计算。
计算图的特征是可以通过传递“局部计算”获得最终结果。“局部”这个词的意思是“与自己相关的某个小范围”。局部计算是指，无论全局发生了什么，都能只根据与自己相关的信息输出接下来的结果。

举个例子：假设（经过复杂的计算）购买的其他很多东西总共花费4000元。这里的重点是，各个节点处的计算都是局部计算。这意味着，例如苹果和其他很多东西的求和运算（4000 + 200 → 4200）并不关心4000这个数字是如何计算而来的，只要把两个数字相加就可以了。换言之，各个节点处只需进行与自己有关的计算（在这个例子中是对输入的两个数字进行加法运算），不用考虑全局。

综上，计算图可以集中精力于局部计算。无论全局的计算有多么复杂，各个步骤所要做的就是对象节点的局部计算。虽然局部计算非常简单，但是通过传递它的计算结果，可以获得全局的复杂计算的结果。

我感觉这和递归分治的思路是差不多的，用小而简单的部分解得出最终复杂问题的解。

因为计算图拥有计算局部性的优点，所以可以通过正向传播和反向传播高效地计算各个变量的导数值，从而高效的完成计算。

链式法则

例如有这么一个函数：

链式法则是关于复合函数的导数的性质，定义如下：
如果某个函数由复合函数表示，则该复合函数的导数可以用构成复合函数的各个函数的导数的乘积表示。


其实就是高数中复合函数求偏导的方法。因此数学基础还是蛮重要的。

反向传播

计算图的反向传播（backward propagation）也就是BP算法，计算的方式：沿着与正方向相反的方向，上游传来的导数乘上局部导数，得出传给下游的导数。

这样通过链式法则，就能够完成反向传播了。
例：


如果看这个例子有点似懂非懂，继续看完下面回过头来看应该就会很明了。

下面介绍一些节点的反向传播的方法

加法节点的反向传播

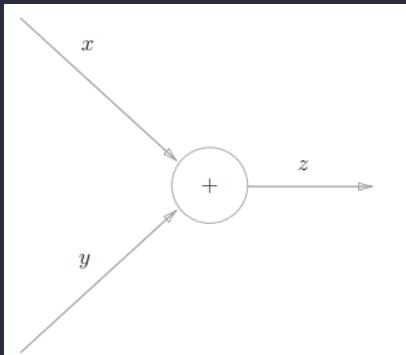
首先来考虑加法节点的反向传播。这里以z = x + y为对象，观察它的反向传播。z = x + y的导数可由下式（解析性地）计算出来。

那么其反向传播就如下:

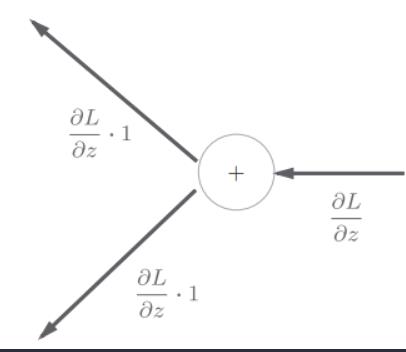
加法节点的反向传播将上游（反向传播右边为上游）的值原封不动地输出到下游

例子：

乘法节点的反向传播

接下来，我们看一下乘法节点的反向传播。这里我们考虑z = xy。这个
式子的导数用式（5.6）表示。

乘法的反向传播会将上游的值乘以正向传播时的输入信号的“翻转值”后传递给下游。翻转值表示一种翻转关系，如下图，正向传播时信号是x的话，反向传播时则是y；正向传播时信号是y的话，反向传播时则是x。

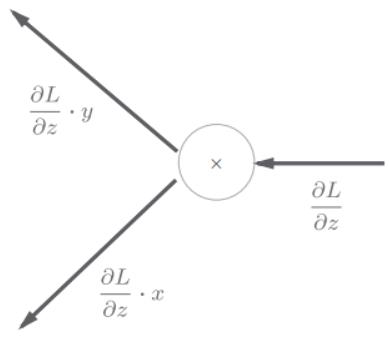
例子：

注意：
因为乘法的反向传播会乘以输入信号的翻转值，所以各自可按1.3 × 5 = 6.5、1.3 × 10 = 13计算。另外，加法的反向传播只是将上游的值传给下游，并不需要正向传播的输入信号。但是，乘法的反向传播需要正向传播时的输入信号值。因此，实现乘法节点的反向传播时，要保存正向传播的输入信号。

小结

其实还会有很多复杂的节点例如log节点，exp节点，/节点等等，其实会计算各种归根到底就是学会如何求这些函数的导数罢了。因此列举加法节点和乘法节点就是为了抛砖引玉，使得我们更形象的理解反向传播。

实例

接下来让我看一些比较复杂的函数的正向传播和反向传播的过程。

Sigmoid函数

Sigmoid函数计算图的正向传播过程：

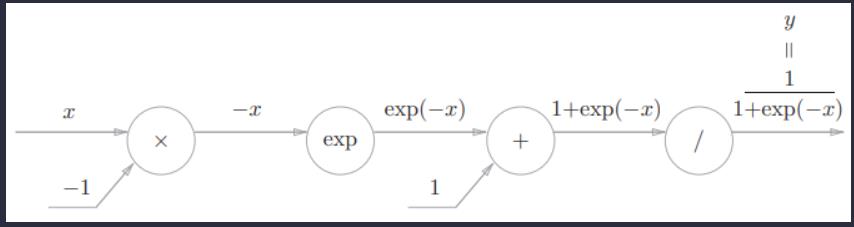
接下来进行反向传播：
为了方便表示，我们令

步骤1
“/”节点表示 ，它的导数可以解析性地表示为下式：

步骤2
“+”节点将上游的值原封不动地传给下游。计算图如下所示。

步骤3
“exp”节点表示y = exp(x)，它的导数由下式表示。

步骤4
“×”节点将正向传播时的值翻转后做乘法运算。因此，这里要乘以−1。

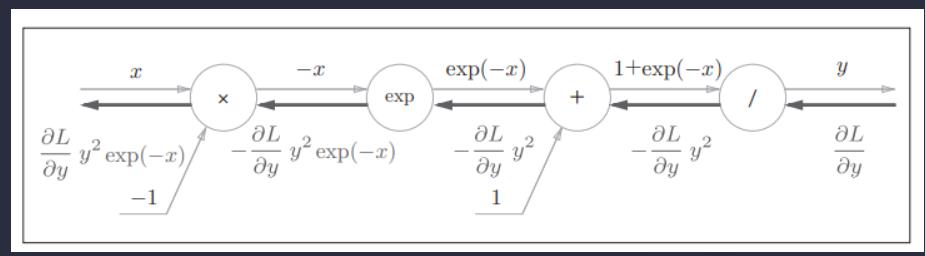
至此，反向传播已经完成。

可以整理一下：

那么我们可以定义一个Sigmoid节点，其反向传播表示如下：

Softmax-with-Loss 层

下面来实现Softmax层。考虑到这里也包含作为损失函数的交叉熵误差（cross entropy error），所以称为“Softmax-with-Loss层”（Softmax函数和交叉熵误差）。

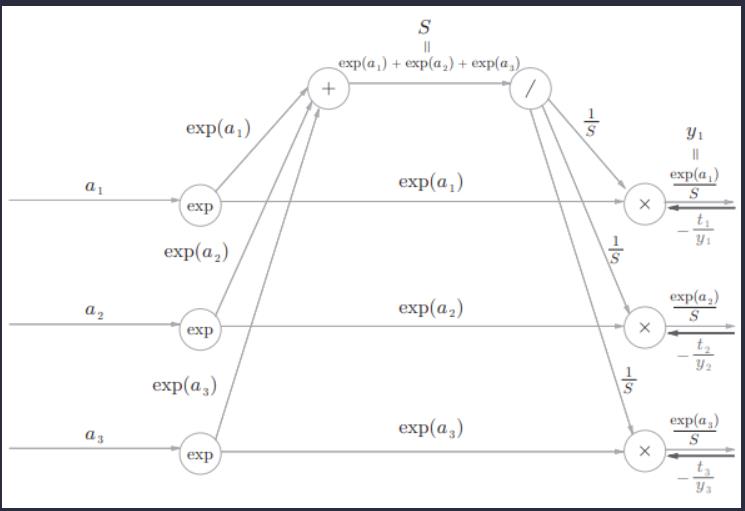
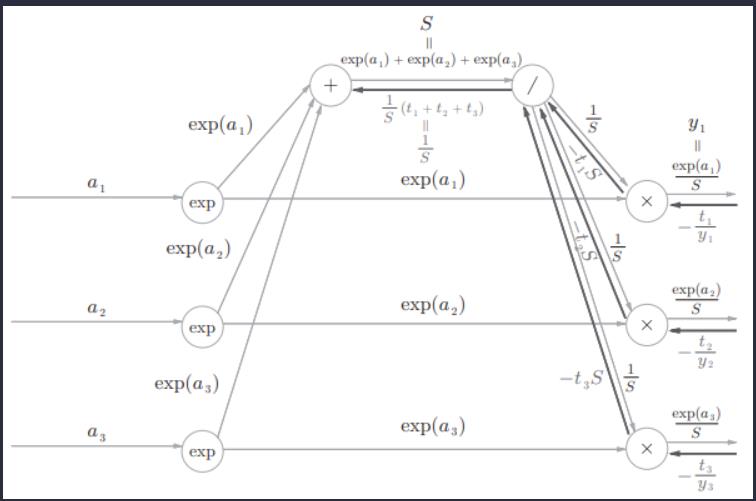
其正向传播如下：

为了方便表示，我们进行一下变量替换如下：

值得注意的是：

因为计算图是局部计算，图中的求导是将前面两个输入节点的看成不同变量的。虽然二者可能相关，但是还是要看成不同的变量，因此需要使用图的乘法规则来进行反向传播的计算。

接下来让我们一步步看看反向传播如何进行。

首先，交叉熵误差的反向传播：


“x”节点上游传过来的导数为1
“+”节点上游传过来的导数为-1
那列“x”节点上游传过来的导数都为-1
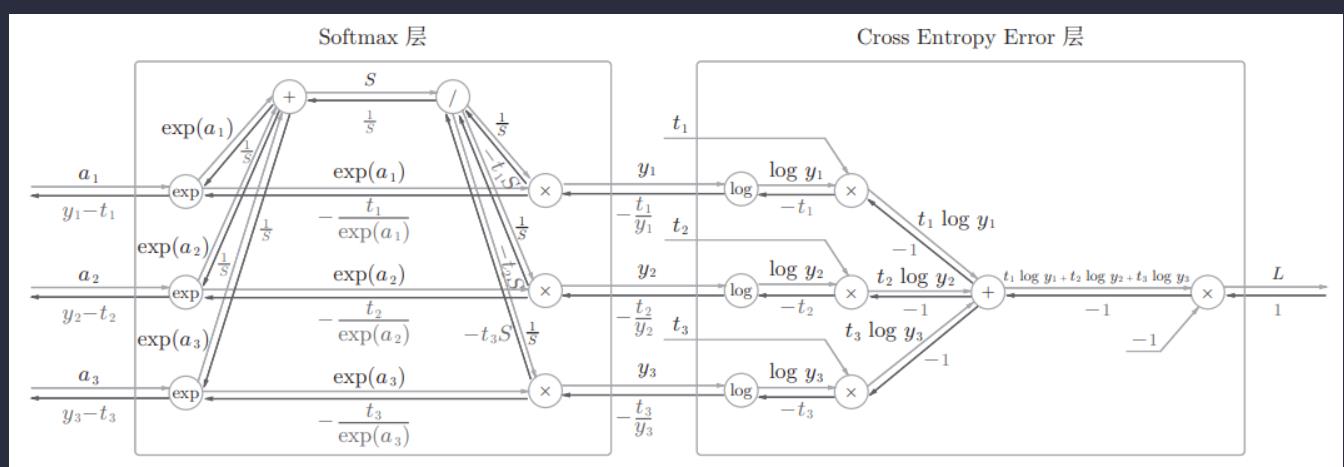
那列log节点上有传过来的导数分别为-t₁、-t₂、-t₃

这里遇到“x”节点。
“×”节点将正向传播的值翻转后相乘。这个过程中会进行下面的计算。

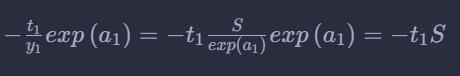
即传给“/”的导数如下：

“+”节点原封不动地传递上游的值。
“×”节点将值翻转后相乘。

因为上面令

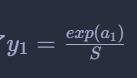
所以

最后exp节点的反向传播如下：

因为exp(x)的导数就是exp(x)，求导还是他本身
所以第一个exp节点最后反向传播的结果如下（正向分流，反向合流）：

因为开始令

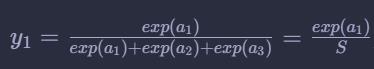
所以最后就是

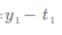
然后剩下的计算都是一样的了。

最终反向传播结果如下：

至此，Softmax-with-Loss 层反向传播的推导完成。

虽然一眼看上去感觉这个计算图十分复杂，但是一步步走过去每一步都是蛮简单的，这就是计算图的局部计算的优势了。

然后现在指定一个学习率lr(0.001等)，假设我们第一个输入是a₁经过反向传播得到的误差为y₁-t₁，那么更新a₁的公式如下：

a₁ ^*= a₁ - lr * (y₁-t₁)

这就是BP算法思想的核心，即先正向传播，计算出误差（损失值，通常会用一个损失函数来衡量预测值与真实值的差距，例如交叉熵函数、均方误差函数等等），然后将误差反向传播，得出每个参数应当做多少的修改以更接近真实值，让误差变小，从而使模型进行训练。

深度学习模型的训练就是依靠误差反向传播调整参数进行的。

参考

深度学习老师的课件。