每日一读Efficient Optimization Methods for Extreme Similarity Learning with Nonlinear Embeddings

Posted 2022-09-27 海轰Pro

目录

• 简介
• 论文简介
• ABSTRACT
• 1 INTRODUCTION
• 2 EXTREME SIMILARITY LEARNING
• 7 CONCLUSIONS
• 读后总结
• 结语

简介

Hello！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～
 
ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，获得过国家奖学金，有幸在竞赛中拿过一些国奖、省奖…已保研
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！
 
唯有努力💪
 
【每日一读】每天浅读一篇论文，了解专业前沿知识，培养阅读习惯（阅读记录 仅供参考）

论文简介

原文链接：https://dl.acm.org/doi/10.1145/3447548.3467363

会议：KDD '21: Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining （CCF A类）

年度：2021年8月14日

ABSTRACT

我们从所有可能的对中使用非线性嵌入模型(例如神经网络)来研究学习相似性问题。

原文：We study the problem of learning similarity by using nonlinear embedding models (e.g., neural networks) from all possible pairs

这个问题因其难以用极端数量的对进行训练而闻名

对于使用线性嵌入的特殊情况，许多研究已经通过考虑某些损失函数和开发有效的优化算法来解决处理所有对的问题

本文旨在扩展一般非线性嵌入的结果

• 首先，我们完成了详细的推导并提供了干净的公式，以有效地计算一些优化算法的构建块，例如函数、梯度评估和 Hessian 向量积。结果使得可以使用许多优化方法进行具有非线性嵌入的极端相似性学习
• 其次，我们详细研究了一些优化方法。由于使用了非线性嵌入，解决了与线性情况不同的实现问题
• 最后，一些方法被证明对于具有非线性嵌入的极端相似性学习非常有效

1 INTRODUCTION

许多应用程序都可以用于学习一对分别称为左右实体的两个实体之间的相似性问题

例如

• 在推荐系统中，用户-项目对的相似性表示用户对项目的偏好
• 在搜索引擎中，查询-文档对的相似度可以用作查询与文档之间的相关性
• 在多标签分类中，对于任何具有高相似度的实例-标签对，都可以将实例分类到标签上

一种流行的相似性学习方法是训练一个嵌入模型作为对中每个实体的表示，这样任何具有高相似性的对都映射到嵌入空间中的两个相近向量，反之亦然

对于嵌入模型的选择，最近的一些工作 [30] 报告了非线性相对于传统线性模型的优越性

应用非线性嵌入模型的一个典型例子是图 1 所示的两塔结构，其中多层神经网络作为每个实体的嵌入模型

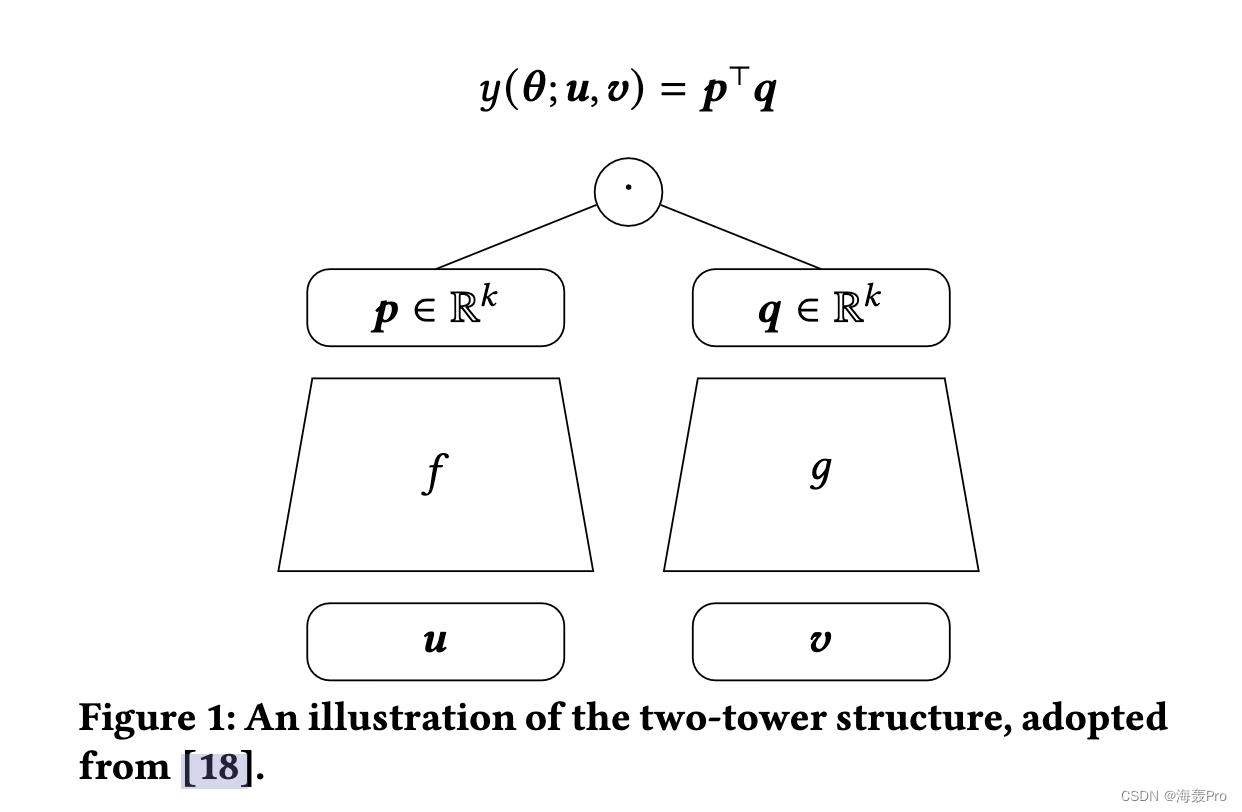
已经报道了在实际应用中的一些成功应用 [7, 11, 12, 23, 24]。

---

虽然许多工作只考虑观察到的对进行相似性学习，但越来越多的工作认为可以通过考虑所有可能的对来实现更好的性能

例如，具有隐式反馈的推荐系统面临一类场景，其中所有观察到的配对都被标记为相似，而不相似的配对则缺失

为了实现更好的相似性学习

• 一个广泛使用的设置 [16, 26, 27] 是将所有未观察到的对包含为不同的对
• 另一个例子是反事实学习 [22, 28]，因为观察到的配对带有由混杂因素引起的选择偏差，消除偏差的有效方法是通过输入标签来额外考虑未观察到的配对

然而，对于许多现实世界的场景，左侧实体的数量 𝑚 和右侧实体的数量 𝑛 都可能是巨大的

学习过程具有挑战性，因为直接应用任何优化算法都会产生令人望而却步的 O (𝑚𝑛) 成本。

为了避免 O (𝑚𝑛) 复杂性，可以对未观察到的对进行二次抽样，但已经表明，这种二次抽样设置不如非二次抽样设置 [17, 25]

我们将极大 𝑚𝑛 对的相似性学习问题称为极端相似性学习

---

为了解决高 O (𝑚𝑛) 复杂性，上述可以处理所有对的工作考虑了具有特定结构的未观察对的损失函数

然后他们能够用更小的 O (𝑚 +𝑛) 复杂度替换 O (𝑚𝑛) 复杂度

特别是，函数值、梯度或其他信息可以在 O (𝑚 + 𝑛) 成本中计算，因此可以考虑各种类型的优化方法

大多数现有的工作考虑线性嵌入（例如，[9,16,25] 中的矩阵分解），其中优化问题通常是多块凸形式

因此，许多人考虑使用分块设置来顺序最小化凸子问题

每个变量块所需的梯度或其他信息也可以在 O (𝑚 + 𝑛) 中计算。

---

如果考虑一般的非线性嵌入，迄今为止很少有工作研究优化算法

这项工作旨在通过以下主要贡献来填补空白:

• 为了计算 O (𝑚 + 𝑛) 成本中的函数值、梯度或其他信息，线性嵌入中的案例扩展似乎是可能的，但还没有详细的推导。 我们完成繁琐的计算并提供干净的配方。 这一结果使得可以使用许多优化方法来进行具有非线性嵌入的极端相似性学习。
• 然后我们详细研究一些优化方法。由于使用了非线性嵌入，解决了一些不同于线性情况的实现问题。最后，一些方法被证明对于具有非线性嵌入的极端相似性学习非常有效。

2 EXTREME SIMILARITY LEARNING

7 CONCLUSIONS

在这项工作中，我们研究了非线性嵌入的极端相似性学习

目标是减轻训练过程中的 O (𝑚𝑛) 成本

虽然这个主题已经针对使用线性嵌入的情况进行了很好的研究，但缺乏对非线性嵌入的系统研究

我们在以下几个方面填补了空白

• 首先，对于优化算法中的重要操作，例如函数和梯度评估，导出了成本为 O (𝑚 + 𝑛) 的干净公式
• 其次，这些公式可以使用许多优化算法来使用非线性嵌入模型进行极端相似性学习。 我们详细讨论了其中一些并检查了实施问题。 实验表明，通过一些算法可以实现高效的训练。

读后总结

这么文章数学性太强了 理解起来好困难

主要是：研究成对节点的相似性学习问题（针对数据量非常大的情况，降低复杂度）

简单阅读了一下，没有理解多少 …

结语

文章仅作为个人学习笔记记录，记录从0到1的一个过程

希望对您有一点点帮助，如有错误欢迎小伙伴指正