数据结构与算法：Bloom Filter(布隆过滤器)解决大数据查重问题

Posted 2022-09-26 _索伦

前言

在内存有所限制的情况下（如上面的面试问题），快速判断一个元素是否在一个集合（容器）当
中，还可以使用布隆过滤器。
布隆过滤器到底是个什么东西呢？
通俗来讲，在使用哈希表比较占内存的情况下，它是一种更高级的“位图法”解决方案，之所以说它更高级，是因为它没有位图法所说的缺陷。

文章目录

• 前言
• BloomFilter
• 场景1：过滤非法网站
• 场景2：Redis缓存中的应用
• BloomFilter黑名单网址示例
• 总结
• end

BloomFilter

1.Bloom Filter是通过一个位数组+k个哈希函数构成的。

图示：首先给出一个位数组，再给出三个哈希函数

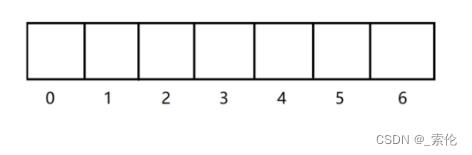
三个哈希函数通过关键字的计算，得到三个位置，这里比如0， 4， 6
那么在位数组上就将对应的位置置为1.

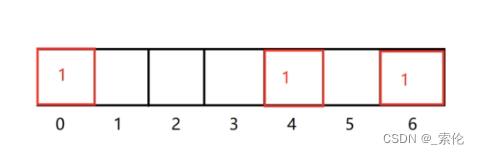
增加一个元素：

1. 经过K个哈希函数计算，得到bitmap位数组里面的一组位序号。
2. 把相应的位置置为1。

搜索一个元素：

1. 经过K个哈希函数计算，得到bitmap位数组里面的一组位序号。
2. 判断上面几个位置的值，如果全是1，证明相应的key存在，如果有一个以上是0，则证明key不在Bloom Filter中。

删除元素？
Bloom Filter不能提供删除操作，因为同一个位置可能是由多个key共用的，就像上面的示例。

Bloom Filter查询一个key值是否存在，如果查出来key经过k个哈希函数处理后，对应的位都是1，能说明这个key存在吗？

其实数据并不一定在，因为映射到的k个位可能被其他数据已经置为1了，所以会存在误判！！！

相反的，如果Bloom Filter说数据不在，那么数据肯定是不存在的！！！

只要能接受一定的误判率，那么这个方法还是很好用的。

场景1：过滤非法网站

提示过滤一些非法的网站，或者钓鱼网站等等

Bloom Filter：把所有可能怀疑有问题的网站的URL添加到布隆过滤器当中，查找当前访问的URL是否在黑名单内，如果存在，会进行提示当前网站有风险，禁止访问。如果URL不存在，那肯定是白名单上的合法网站，可以直接访问。

场景2：Redis缓存中的应用

如图：
有客户端请求进入网络层 ⇒ 业务层，然后是先去redis的缓存层查询，如果key存在，则直接返回，如果不存在，才进入数据库层来找到key，并将value在缓存层缓存，然后返回。
redis缓存是内存IO，数据库是磁盘IO，磁盘IO是比内存IO要慢几十上百万倍，

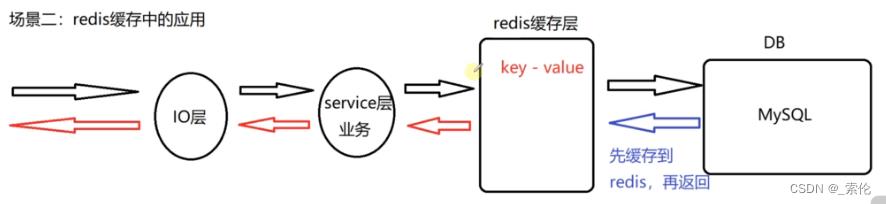
场景：
查key到底存不存在，而且效率要求高，最好还省内存；
那么Bloom Filter首先使用 setBit(key)，将key存放起来；
通过getBit(key)来查找，如果不存在，则去DB层，然后缓存到redis，再返回；getBit(key)如果存在，则redis中找到key，直接返回。

BloomFilter黑名单网址示例

在这里先实现一个Bloom Filter，提供增加和查询两个接口，然后再实现一个黑名单，将黑名单类提供给客户，提供add()和query()方法，底层也是一个Bloom Filter类型的变量。

#include <iostream>
#include <vector>
#include <string>

#include "stringhash.h"

using namespace std;

// 布隆过滤器
class BloomFilter

public:
	BloomFilter(int bitSize = 1471)
		: bitSize_(bitSize)
	
		bitMap_.resize(bitSize_ / 32 + 1);
	

public:
	// 添加元素
	void setBit(const char* str)
	
		// 计算k组哈希函数的值
		int idx1 = BKDRHash(str) % bitSize_;
		int idx2 = RSHash(str) % bitSize_;
		int idx3 = APHash(str) % bitSize_;

		// 把相应的idx1 idx2 idx3这几个位置为1
		int index = 0;
		int offset = 0;

		index = idx1 / 32;
		offset = idx1 % 32;
		bitMap_[index] |= (1 << offset);

		index = idx2 / 32;
		offset = idx2 % 32;
		bitMap_[index] |= (1 << offset);

		index = idx3 / 32;
		offset = idx3 % 32;
		bitMap_[index] |= (1 << offset);
	

	// 查询元素
	bool getBit(const char* str)
	
		// 计算k组哈希函数的值
		int idx1 = BKDRHash(str) % bitSize_;
		int idx2 = RSHash(str) % bitSize_;
		int idx3 = APHash(str) % bitSize_;

		int index = 0;
		int offset = 0;

		index = idx1 / 32;
		offset = idx1 % 32;
		if (0 == (bitMap_[index] & (1 << offset)))
		
			// 具体业务，根据需求更改
			cout << "该网址安全，是否继续？" << endl;
			return false;
		

		index = idx2 / 32;
		offset = idx2 % 32;
		if (0 == (bitMap_[index] & (1 << offset)))
		
			// 具体业务，根据需求更改
			cout << "该网址安全，是否继续？" << endl;
			return false;
		

		index = idx3 / 32;
		offset = idx3 % 32;
		if (0 == (bitMap_[index] & (1 << offset)))
		
			// 具体业务，根据需求更改
			cout << "该网址安全，是否继续？" << endl;
			return false;
		

		// 根据业务需求更改
		cout << "该网址非法访问！" << endl;
		return true;
	
private:
	int bitSize_;	// 位图的长度
	vector<int> bitMap_;	// 位图数组
;

class BlackList

public:
	// 添加非法URL
	void add(string url)
	
		blackList_.setBit(url.c_str());
	

	// 查询
	bool query(string url)
	
		return blackList_.getBit(url.c_str());
	
private:
	BloomFilter blackList_;
;

int main(void)

	BlackList list_;
	list_.add("https://www.baidu.com");
	list_.add("https://www.tmall.com");
	list_.add("https://www.360.com");
	list_.add("https://tencent.com");

	list_.query("https://www.tmall.com");
	list_.query("https://www.alibaba.com");

	return 0;

总结

这里总结一下Bloom Filter的注意事项：

1. Bloom Filter是通过一个位数组 + k个哈希函数构成的。
2. Bloom Filter的空间和时间利用率都很高，但是它有一定的错误率，虽然错误率很低，Bloom
   Filter判断某个元素不在一个集合中，那该元素肯定不在集合里面；Bloom Filter判断某个元素在一
   个集合中，那该元素有可能在，有可能不在集合当中。
3. Bloom Filter的查找错误率，当然和位数组的大小，以及哈希函数的个数有关系，具体的错误率
   计算有相应的公式（错误率公式的掌握看个人理解，不做要求）。
4. Bloom Filter默认只支持add增加和query查询操作，不支持delete删除操作（因为存储的状态位
   有可能也是其它数据的状态位，删除后导致其它元素查找判断出错）。
   Bloom Filter增加元素的过程：把元素的值通过k个哈希函数进行计算，得到k个值，然后把k当作
   位数组的下标，在位数组中把相应k个值修改成1。
   Bloom Filter查询元素的过程：把元素的值通过k个哈希函数进行计算，得到k个值，然后把k当作
   位数组的下标，看看相应位数组下标标识的值是否全部是1，如果有一个为0，表示元素不存在
   （判断不存在绝对正确）；如果都为1，表示元素存在（判断存在有错误率）。

很显然，过小的布隆过滤器很快所有的bit位均为1，那么查询任何值都会返回“可能存在”，起不到
过滤的目的。布隆过滤器的长度会直接影响误报率，布隆过滤器越长其误报率越小。另外，哈希函
数的个数也需要权衡，个数越多则布隆过滤器bit位置为1的速度越快，且布隆过滤器的效率越低；
但是如果太少的话，那误报率就会变高。

end

关于上面示例的这些哈希函数，在此附一个头文件。。

#pragma once

/// @brief BKDR Hash Function  
/// @detail 本 算法由于在Brian Kernighan与Dennis Ritchie的《The C Programming Language》一书被展示而得 名，是一种简单快捷的hash算法，也是Java目前采用的字符串的Hash算法（累乘因子为31）。  
template<class T>
size_t BKDRHash(const T* str)

    register size_t hash = 0;
    while (size_t ch = (size_t)*str++)
    
        hash = hash * 131 + ch;   // 也可以乘以31、131、1313、13131、131313..  
        // 有人说将乘法分解为位运算及加减法可以提高效率，如将上式表达为：hash = hash << 7 + hash << 1 + hash + ch;  
        // 但其实在Intel平台上，CPU内部对二者的处理效率都是差不多的，  
        // 我分别进行了100亿次的上述两种运算，发现二者时间差距基本为0（如果是Debug版，分解成位运算后的耗时还要高1/3）；  
        // 在ARM这类RISC系统上没有测试过，由于ARM内部使用Booth's Algorithm来模拟32位整数乘法运算，它的效率与乘数有关：  
        // 当乘数8-31位都为1或0时，需要1个时钟周期  
        // 当乘数16-31位都为1或0时，需要2个时钟周期  
        // 当乘数24-31位都为1或0时，需要3个时钟周期  
        // 否则，需要4个时钟周期  
        // 因此，虽然我没有实际测试，但是我依然认为二者效率上差别不大          
    
    return hash;

/// @brief SDBM Hash Function  
/// @detail 本算法是由于在开源项目SDBM（一种简单的数据库引擎）中被应用而得名，它与BKDRHash思想一致，只是种子不同而已。  
template<class T>
size_t SDBMHash(const T* str)

    register size_t hash = 0;
    while (size_t ch = (size_t)*str++)
    
        hash = 65599 * hash + ch;
        //hash = (size_t)ch + (hash << 6) + (hash << 16) - hash;  
    
    return hash;

/// @brief RS Hash Function  
/// @detail 因Robert Sedgwicks在其《Algorithms in C》一书中展示而得名。  
template<class T>
size_t RSHash(const T* str)

    register size_t hash = 0;
    size_t magic = 63689;
    while (size_t ch = (size_t)*str++)
    
        hash = hash * magic + ch;
        magic *= 378551;
    
    return hash;

/// @brief AP Hash Function  
/// @detail 由Arash Partow发明的一种hash算法。  
template<class T>
size_t APHash(const T* str)

    register size_t hash = 0;
    size_t ch;
    for (long i = 0; ch = (size_t)*str++; i++)
    
        if ((i & 1) == 0)
        
            hash ^= ((hash << 7) ^ ch ^ (hash >> 3));
        
        else
        
            hash ^= (~((hash << 11) ^ ch ^ (hash >> 5)));
        
    
    return hash;

/// @brief JS Hash Function  
/// 由Justin Sobel发明的一种hash算法。  
template<class T>
size_t JSHash(const T* str)

    if (!*str)        // 这是由本人添加，以保证空字符串返回哈希值0  
        return 0;
    register size_t hash = 1315423911;
    while (size_t ch = (size_t)*str++)
    
        hash ^= ((hash << 5) + ch + (hash >> 2));
    
    return hash;

/// @brief DEK Function  
/// @detail 本算法是由于Donald E. Knuth在《Art Of Computer Programming Volume 3》中展示而得名。  
template<class T>
size_t DEKHash(const T* str)

    if (!*str)        // 这是由本人添加，以保证空字符串返回哈希值0  
        return 0;
    register size_t hash = 1315423911;
    while (size_t ch = (size_t)*str++)
    
        hash = ((hash << 5) ^ (hash >> 27)) ^ ch;
    
    return hash;

/// @brief FNV Hash Function  
/// @detail Unix system系统中使用的一种著名hash算法，后来微软也在其hash_map中实现。  
template<class T>
size_t FNVHash(const T* str)

    if (!*str)   // 这是由本人添加，以保证空字符串返回哈希值0  
        return 0;
    register size_t hash = 2166136261;
    while (size_t ch = (size_t)*str++)
    
        hash *= 16777619;
        hash ^= ch;
    
    return hash;

/// @brief DJB Hash Function  
/// @detail 由Daniel J. Bernstein教授发明的一种hash算法。  
template<class T>
size_t DJBHash(const T* str)

    if (!*str)   // 这是由本人添加，以保证空字符串返回哈希值0  
        return 0;
    register size_t hash = 5381;
    while (size_t ch = (size_t)*str++)
    
        hash += (hash << 5) + ch;
    
    return hash;

/// @brief DJB Hash Function 2  
/// @detail 由Daniel J. Bernstein 发明的另一种hash算法。  
template<class T>
size_t DJB2Hash(const T* str)

    if (!*str)   // 这是由本人添加，以保证空字符串返回哈希值0  
        return 0;
    register size_t hash = 5381;
    while (size_t ch = (size_t)*str++)
    
        hash = hash * 33 ^ ch;
    
    return hash;

/// @brief PJW Hash Function  
/// @detail 本算法是基于AT&T贝尔实验室的Peter J. Weinberger的论文而发明的一种hash算法。  
template<class T>
size_t PJWHash(const T* str)

    static const size_t TotalBits = sizeof(size_t) * 8;
    static const size_t ThreeQuarters = (TotalBits * 3) / 4;
    static const size_t OneEighth = TotalBits / 8;
    static const size_t HighBits = ((size_t)-1) << (TotalBits - OneEighth);

    register size_t hash = 0;
    size_t magic = 0;
    while (size_t ch = (size_t)*str++)
    
        hash = (hash << OneEighth) + ch;
        if ((magic = hash & HighBits) != 0)
        
            hash = ((hash ^ (magic >> ThreeQuarters)) & (~HighBits));
        
    
    return hash;

/// @brief ELF Hash Function  
/// @detail 由于在Unix的Extended Library Function被附带而得名的一种hash算法，它其实就是PJW Hash的变形。  
template<class T>
size_t ELFHash(const T* str)

    static const size_t TotalBits = sizeof(size_t) * 8;
    static const size_t ThreeQuarters = (TotalBits * 3) / 4;
    static const size_t OneEighth = TotalBits / 8;
    static const size_t HighBits = ((size_t)-1) << (TotalBits - OneEighth);
    register size_t hash = 0;
    size_t magic = 0;
    while (size_t ch = (size_t)*str++)
    
        hash = (hash << OneEighth) + ch;
        if ((magic = hash & HighBits) != 0)
        
            hash ^= (magic >> ThreeQuarters);
            hash &= ~magic;
        
    
    return hash;