概率论—高中基础知识

Posted 2022-09-20 LuckyZhouStar

概率论包括随机事件及其概率、随机变量及其概率分布、多维随机变量及其概率分布、随机变量的数字特征及大数定律和中心极限定理。共五章，重点第一、二章，数理统计包括样本与统计量，参数估计和假设检验、回归分析。重点是参数估计。

---

一、加法原则
引例一，从北京到上海的方法有两类：第一类坐火车，若北京到上海有早、中、晚三班火车分别记作火 ₁、火₂、火₃，则坐火车的方法有3种；第二类坐飞机，若北京到上海的飞机有早、晚二班飞机，分别记作飞₁、飞₂。问北京到上海的交通方法共有多少种。

解：
从北京到上海的交通方法共有火₁、火₂、火₃、飞₁、飞₂共5种。它是由第一类的3种方法与第二类的2种方法相加而成。
一般地有下面的加法原则：
办一件事，有m类办法，其中：
第一类办法中有n₁种方法；
第二类办法中有n₂种方法；
……
第m类办法中有nₘ种方法；
则办这件事共有种方法

二、乘法原则
引例二，从北京经天津到上海，需分两步到达。
第一步从北京到天津的汽车有早、中、晚三班，记作汽₁、汽₂、汽₃ 第二步从天津到上海的飞机有早、晚二班，记作飞₁、飞₂ 问从北京经天津到上海的交通方法有多少种？

解：从北京经天津到上海的交通方法共有：
①汽₁飞₁，②汽₁飞₂ ，③汽₂ 飞₁，④汽₂ 飞₂ ，⑤汽₃飞₁，⑥汽₃飞₂ 。共6种，它是由第一步由北京到天津的3种方法与第二步由天津到上海的2种方法相乘3×2=6生成。 一般地有下面的乘法原则：
办一件事，需分m个步骤进行，其中：
第一步骤的方法有n₁种；
第二步骤的方法有n₂种；
……
第m类办法中有nₘ种方法；
则办这件事共有种方法

三、排列（数）
从n个不同的元素中，任取其中m个排成与顺序有关的一排的方法数叫排列数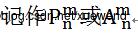，，公式：

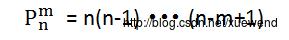
例如：

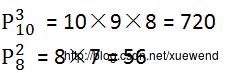
四、组合（数）

例一，袋中有8个球，从中任取3个球，求取法有多少种？
解：任取出三个球与所取3个球顺序无关，故方法数为组合数为种。

例二，袋中五件不同正品，三件不同次品（√√√√√×××）从中任取3件，求所取3件中有2件正品1件次品的取法有多少种？
解：
第一步在5件正品中取2件，取法有：种
第二步在3件次品中取1件，取法有： 种
由乘法原则，取法共有10×3=30（种）