计算机编码--为什么整数中负数的除法和右移不是一回事

Posted 2020-11-18 tlz888

缘起

　　最近在看卡耐基梅隆大学的【深入理解计算机系统实验】之datalab时，遇到一个题目：

 1 /* 
 2  * divpwr2 - Compute x/(2^n), for 0 <= n <= 30 
 3  *  Round toward zero 
 4  *   Examples: divpwr2(15,1) = 7, divpwr2(-33,4) = -2 
 5  *   Legal ops: ! ~ & ^ | + << >> 
 6  *   Max ops: 15 
 7  *   Rating: 2 
 8  */  
 9 int divpwr2(int x, int n) {  
10 
11 } 

即只能用题目提供的操作实现 x/(2^n) 的计算。对于正数，没什么可说的，直接x>>n即可。

但是负数也是这样吗，仔细一看，才发现  x/(2^n) 和 x>>n不是一回事。

比如 -33/(2^4) = -2, 但是另一方面，-33的编码为0xFFFFFFDF，右移4位变成0xFFFFFFFD，即-3，显然不一致。

 

思考中的犯傻

　　对于上述问题，在做最后的解释前，先插入一段我的思考过程，主要是记录其中的犯傻之处。

由于计算机中整数的表示法为 2的补码（two‘s complemet representation），如下公式：

    

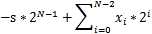
其中s为符号位，x为其他位，N为位数。

对于正数，s为0，只剩后面的求和项，除以(2^n)的话，从公式上看确实是直接右移n位即可。

接着这个思路，我就想，那么负数除以(2^n)等于：

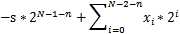
其中第二项跟正数一样，右移n位即可，第一项是什么呢？c语言中的int类型位数太长，这里简单以8位代替。

-2^（8-1）   = -128(十进制) = 1000 0000（二进制）

-2^（8-1-1）= -64(十进制) =   1100 0000（二进制）

-2^（8-1-2）= -32(十进制) =   1110 0000（二进制）

也就是说，前面说的第一项其实也是原式的第一项右移n位。所以，总体来说负数除法也是右移。

但是，这个结论显然与-33/(2^4)那个例子矛盾，可是错误在哪儿呢？

其实，错误就在于把x掰开成两个，然后整除2^n，在把结果加起来，这个过程与x直接整除2^n是不等价的。

比如：6/2=3,但是 3/2+3/2=1+1=2。虽然错误很明显，但是一开始思考的时候却犯傻了。

 

原因应该是什么

负数除法与移位不同的原因用下面一张图就能说明白：

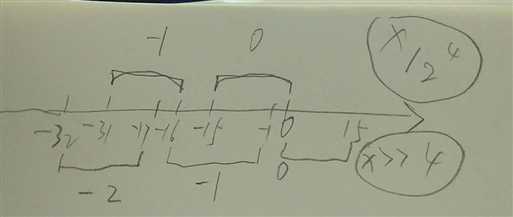
　　如图所示，中间是一条数轴，数轴上面是x与x/(2^4)的对应关系，下面是x与x>>4的对应关系，

设  x/(2^4)=f(x)>>4，那么从上图可以看出，当x/(2^4)得到-1时，f(x)>>4为了得到-1，f(x)要比x向右移动15，或2^4-1。

图中具体是-16->-1或者-31->-16。

　　因此，x / (2^n) = (x + (2^n-1)) >> n，所以，datalab那个题目的答案可以是：

1 int divpwr2(int x, int n) {  
2     //all zeros or all ones  
3     int signx=x>>31;  
4     //int mask=(1<<n)+(-1);  
5     int mask=(1<<n)+(~0);  
6     int bias=signx&mask;  
7     return (x+bias)>>n;  
8 } 

 

参考文章：

（1）负数的除法和右移的区别；

（2）datalab 深入理解计算机系统实验。