字符贡献度问题

Posted 2022-09-07 白龙码~

文章目录

• 字符贡献度问题
• • 一、问题引入
  • 二、问题分析
  • 三、代码实现

字符贡献度问题

一、问题引入

对于一个字符串，如ABA，求出其中只出现一次的字符的个数如何求取？easy，哈希表统计一下就好。

那么，对于ABA的所有子串，其中每个子串中只出现一次的字符个数之和如何求取？

---

二、问题分析

以ABA为例，一般的暴力算法是：求出所有子串，即A,B,A,AB,BA,ABA，然后对于每个子串，都使用哈希表计算只出现一次的字符个数。

很明显，该算法的时间复杂度为：
$$[C(N,1)+C(N,2)+C(N,3)+...+C(N,N)]\ast N=N\ast (2^N-1)$$
有没有更好的方法？

我们不妨考虑：什么时候子串的某个字符是唯一的？设原字符串为s[0, n)，子串为s[l, r]，出现一次的字符所在下标为i。那么表明，该字符上次出现的下标必然在l之前，下次出现的下标必然在r之后，因此才能保证[l, r]中该字符只出现一次。

那么我们再换一个角度：假设字符c上次出现的下标为Li，下次出现的下标为Ri，则对于s[Li, Ri]内的所有子串，字符c都能贡献一个只出现一次的次数，对否？那么整个问题就变成了，s[Li, Ri]内有多少个子串包含字符c！

我们以字符串AXABCA为例，计算该字符串中有多少个子串包含i=2处的字符A：

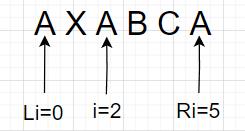
已知，s[1, 4]只包含一个字符A，我们可以将该字符串分为三部分：[1, 1], 2, [3, 4]，其中[1, 1]和[3, 4]不包含A。那么包含A的子串可以从[1, 1]和[3, 4]中抽取，但是必须保证[1, 1]中抽取的字符串必须以1结尾，因为它要与i=2处的A相连。同样的，[3, 4]中抽取的字符串必须以3开头，因为它要与i=2处的A相连。

所以，[1, 1]可以抽取s[1,1]、空串，[3, 4]可以抽取空串、s[3, 3]、s[3, 4]，总计2*3=6个子串。

那么从代数的角度，子串的个数就是[i - Li]*(Ri - i)。

因此，对于字符串中的每一个字符，我们求出它能为多少个子串贡献只出现一次的次数，就相当于变相地求解了整个复杂的问题了！

---

三、代码实现

题目出自LeetCode 828. 统计子串中的唯一字符

int uniqueLetterString(string s) 

    // 记下标i处的字符c左边出现c的下标为i1，右边出现c的下标i2
    // XBAXCA   i1=-1 i=2 i2=5  
    // 则该字符为(i-i1)*(i2-i)个子串贡献一个唯一字符
    int n = s.size();
    vector<int> dic(26, -1);
    vector<int> left(n); // 记录每个字符，左边出现同样字符的最近下标
    vector<int> right(n); // 记录每个字符，右边出现同样字符的最近下标
    for (int i = 0; i < n; ++i)
    
        left[i] = dic[s[i] - 'A'];
        dic[s[i] - 'A'] = i;
    
    dic = vector<int>(26, n);
    for (int i = n - 1; i >= 0; --i)
    
        right[i] = dic[s[i] - 'A'];
        dic[s[i] - 'A'] = i;
    

    int res = 0;
    for (int i = 0; i < n; ++i)
    
    	res += (i - left[i]) * (right[i] - i);
    

    return res;