[LeetCode]剑指 Offer 11. 旋转数组的最小数字

Posted 2022-09-06 Spring-_-Bear

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。

给你一个可能存在重复元素值的数组 numbers ，它原来是一个升序排列的数组，并按上述情形进行了一次旋转。请返回旋转数组的最小元素。例如，数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一次旋转，该数组的最小值为 1。

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

示例 1：

输入：numbers = [3,4,5,1,2]
输出：1

示例 2：

输入：numbers = [2,2,2,0,1]
输出：0

提示：

• n == numbers.length
• 1 <= n <= 5000
• -5000 <= numbers[i] <= 5000
• numbers 原来是一个升序排序的数组，并进行了 1 至 n 次旋转

题解：

排序数组的查找问题首先考虑使用二分法解决，其可将遍历的线性级别时间复杂度降低至对数级别 。

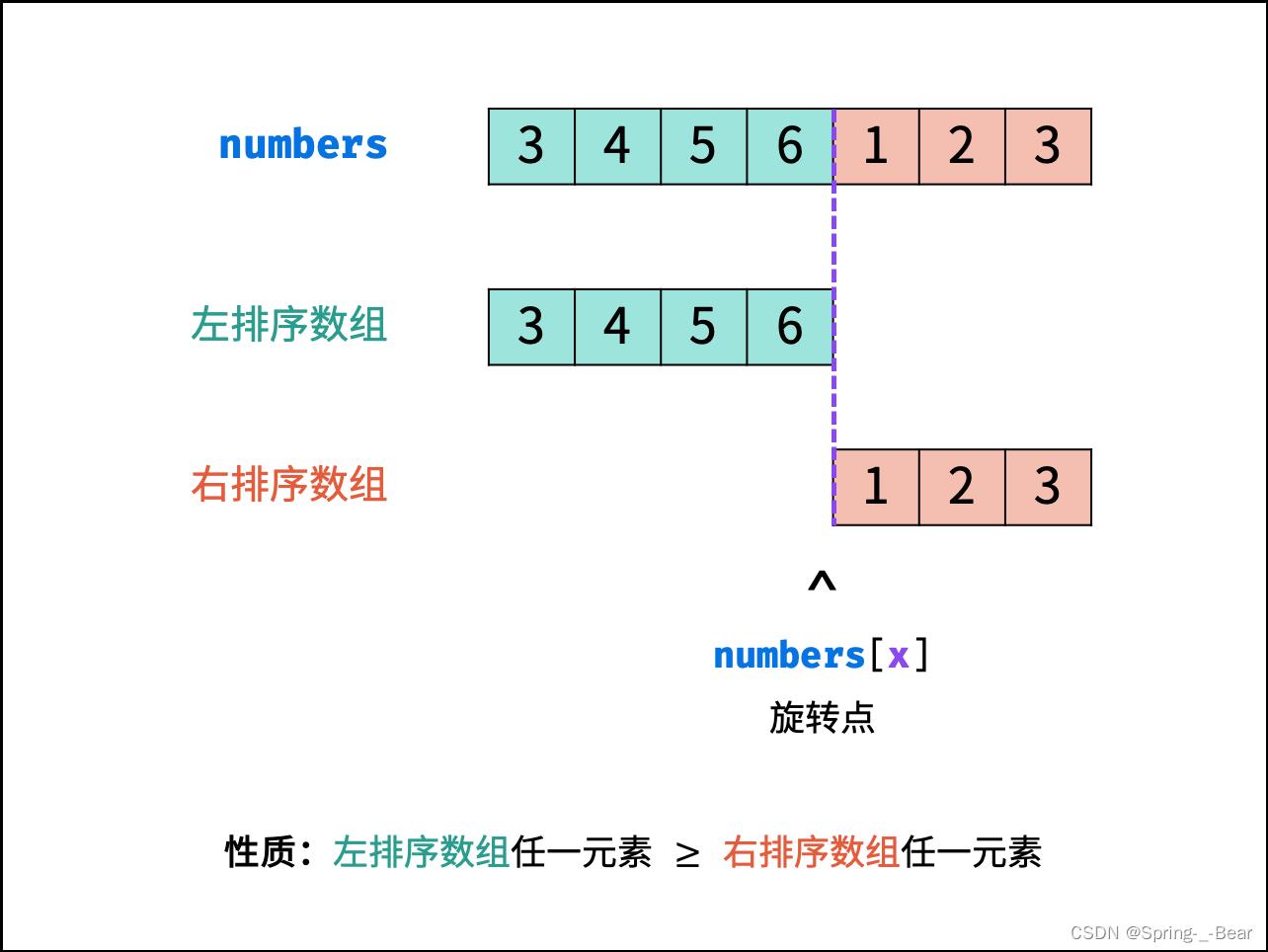
算法流程：

• 初始化： 声明 i, j 双指针分别指向 numbers 数组左、右两端
• 循环二分： 设 m = (i + j) / 2 为每次二分的中点（ / 代表向下取整除法，因此恒有 i ≤ m <j），可分为以下三种情况：
  1. 当 nums[m] > nums[j] 时： m 落在左排序数组中，即旋转点 x 一定在 [m + 1, j] 闭区间内，因此执行 i = m + 1
  2. 当 nums[m] < nums[j] 时： m 落在右排序数组中，即旋转点 x 一定在 [i, m] 闭区间内，因此执行 j = m
  3. 当 nums[m] = nums[j] 时： 无法判断 m 在哪个排序数组中，即无法判断旋转点 x 在哪个区间中。解决方案： 执行 j = j - 1 缩小判断范围

	/**
     * 剑指 Offer 11. 旋转数组的最小数字
     */
    public int minArray(int[] numbers) 
        int i = 0;
        int j = numbers.length - 1;
        while (i < j) 
            int m = (i + j) / 2;
            if (numbers[m] > numbers[j]) 
                i = m + 1;
             else if (numbers[m] < numbers[j]) 
                j = m;
             else 
                j--;
            
        
        return numbers[i];
    

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/xuan-zhuan-shu-zu-de-zui-xiao-shu-zi-lcof