《Translating Images into Maps》论文笔记

Posted 2022-08-24 m_buddy

参考代码：translating-images-into-maps

1. 概述

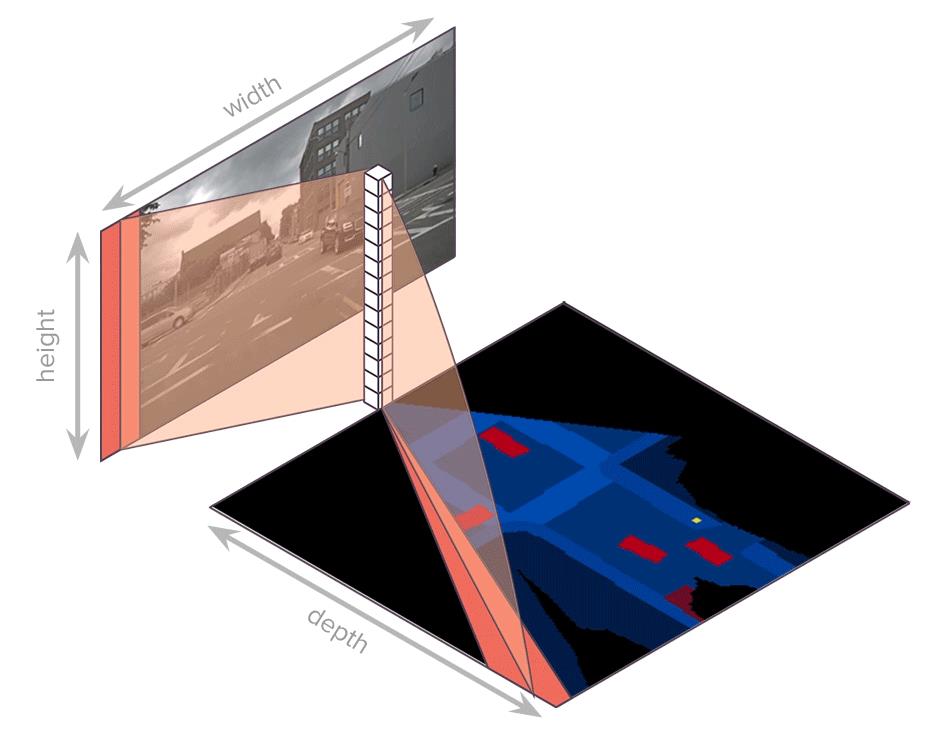
介绍：在这篇文章中提出了一种新的bev特征抽取方法，其思想是在图像特征的w维度上进行展开，对每个在w维度上展开的特征通过非线性映射的关系建立其到对应bev区域的映射，只不过这里的bev上的映射区域是从原点出发的一个扇形区域（文章也将其称之为polar ray），也就通过这样类似扫描的方式建立起w维度展开序列特征到bev特征的对应关系。此外，对于最终映射bev特征会根据距离的远近划分到不同stage的图像特征上去，也就是说对于越远的的地方使用的图像特征分辨率也就越大。除了对当前时间戳上的多帧图像映射到bev下，还通过关联时序特征的方式引入时序信息，从而提供更加丰富的感知表达。

使用该工程下的GIF动图更加能形象表达序列映射的对应关系：

2. 方法设计

2.1 网络pipeline

文章的主体结构见下图所示：

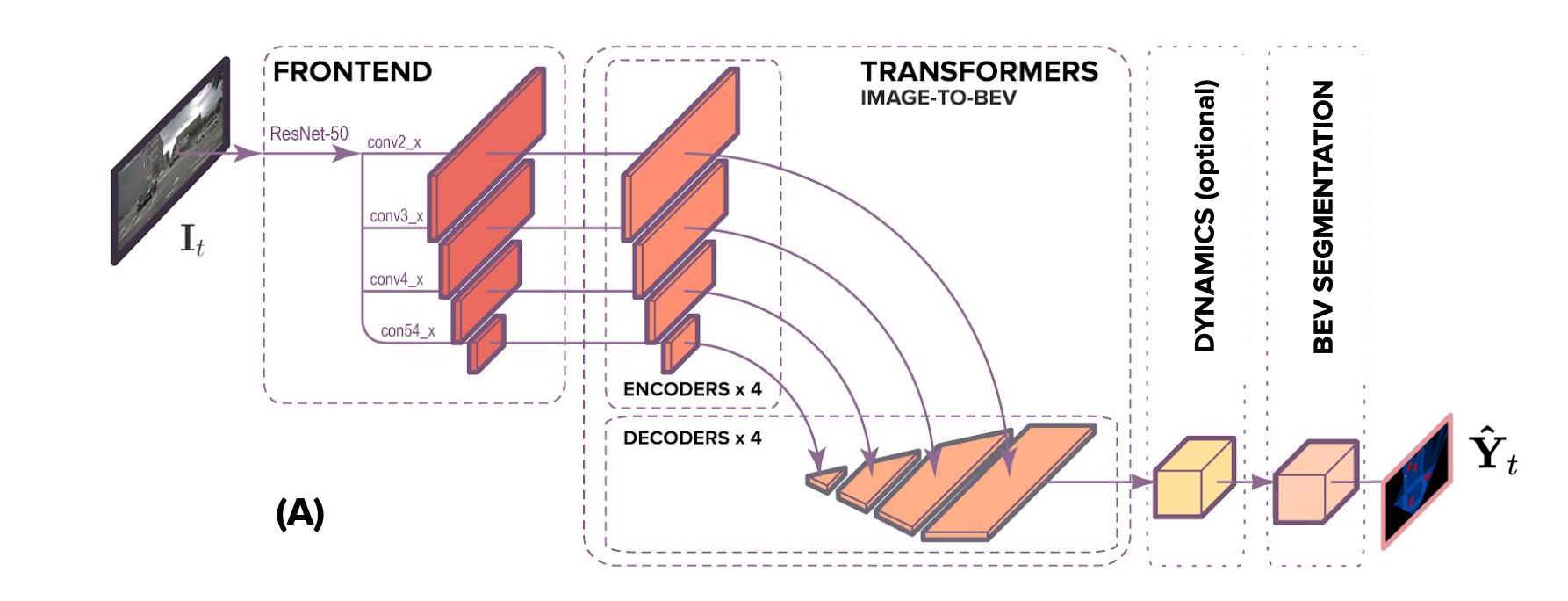
通过分析上图中数据的流向可以将网络的处理流程划分为如下几个步骤：

• Step1：通过如CNN或者Transformer这样的特征抽取网络抽取输入图像特征 $S^I\in R^{C\ast H\ast W}$；
• Step2：按照距离的远近将不同距离段的bev划分到不同stage的图像特征上去，并通过非线性形映射得到对应bev特征$S^{(\varphi (BEV))}$；
• Step3（optional）：这一步是可选的，主要用于去关联时序信息，对应上面的DYNAMICS操作；
• Step4 ：在得到的bev特征上完成下游任务，比如分割；

2.2 图像特征到BEV的特征转换

文章中提到的bev特征（polar ray）转换是通过在w维度上进行序列预测的方式得到的，也就是下图中的形式：

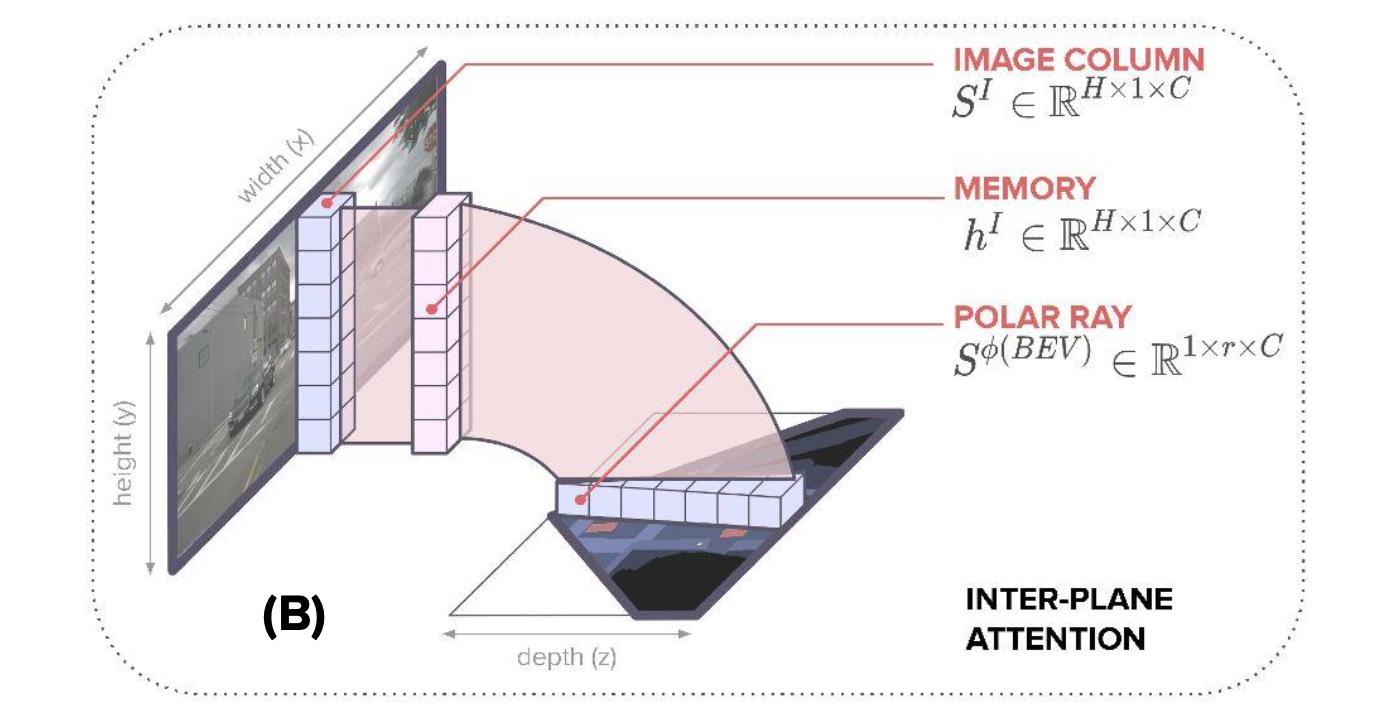
输入的一列图像特征会经过非线性映射得到特征$h\in R^{H\ast C}$，之后通过attention的映射得到bev特征$y\in R^{r\ast C}$，其中$r$就是代表bev特征（polar ray）表达的长度（或者理解为场景深度）。此外，这里是通过queries的形式表达需要表达的bev特征，其构建过程不仅考虑了bev特征长度，还考虑了角度信息，也就是这两者统一参与了queries的构建过程。参考：

# src/model/positional_encoding.py#L69
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)  # 角度信息
div_term = torch.exp(
    torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model)
)
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.sin(position * div_term)

2.2.1 基于标准attention的特征转换

这里的attention包含两个部分：图像特征上的attention和polar-ray上的attention。这两个分别完成的是图像特征到bev特征（polar ray）映射和polar ray特征的表达优化。这里虽然没有显式去使用depth信息，其实是depth隐式编码在了attention的操作中了。

图像特征上的attention：
这里输入是在w维度上进行划分之后的图像特征，其经过非线性层之后得到memory特征$h$，之后会与query做attention，从而得到polar ray特征表达。首先对输入的图像特征和query做映射：
$$Q(y_i)=y_i{W}_Q,K(h_i)=h_i{W}_K,W_Q,W_K\in R^{C\ast D}$$
之后图像特征上的每个点和polar-ray上的每个点的映射关系转换为概率表达：
$${\alpha }_{i,j}=\frac{exp(e_{i,j})}{{\sum }_{k=1}^{H}exp(e_{i,k})}$$
从而得到pola-ray上其中一个点的最后表达：
$$c_i=\sum _{j=1}^H{\alpha }_{i,j}K(h_j)$$
之后，polar-ray特征经过非线性映射得到最后结果：
$$S_i^{\varphi (BEV)}=g(c),c=c_1,\dots ,c_r$$

polar-ray上的attention：
这里的attention是建立ray和ray之间的关联（也就是self-attention），从而去优化bev的特征表达，则这里可以借鉴上述表达中关于attention的描述。

2.2.2 基于单调注意力机制的特征转换

在上述的特征转换过程中是通过学习的方式得到bev特征的，但是构建特征关联权重的时候其实忽略了一个重要的发现：在图像中从底部出发，越往上其真实的距离也是越远的，也就是图像的高度跟实际的深度是具有一定关联的，因而文章这里引入了一种单调attention机制（MA，Monotonic attention），希望借此来实现对深度的显式表达，从而用于生成更好的bev特征表达。

对于上述提到的单调注意力机制，其实就是依据query的不同在输入图像特征上去选择对应范围的特征表达，因而这里在上述2.2.1节图像特征attention基础上添加了一个确定停止位置$t_i$（相当于通过这个排除掉一些特征，从而由于全部图像特征加入attention导致的过拟合情况）的概率分布表达：
$$p_{i,j}=sigmoid(Energy(y_i,h_j))$$
那么在图像特征位置$j$处的配置权重被描述为：
$${\alpha }_{i,j}=p_{i,j}((1-p_{i,j-1})\frac{{\alpha }_{i,j-1}}{p_{i,j-1}}+{\alpha }_{i-1,j})$$
则结合2.2.1节中对于概率的计算在添加了截止信息概率之后：
$${\beta }_{i,j}=\sum _{k=j}^H(\frac{{\alpha }_{i,k}exp(e_{i,k})}{{\sum }_{l=1}^{k}exp(e_{i,l})})$$
最后polar-ray上的一个点的输出表达：
$$c_i=\sum _{j=1}^{H以上是关于《Translating\; Images\; into\; Maps》论文笔记的主要内容，如果未能解决你的问题，请参考以下文章}$$

Python文档阅读笔记-Turn Images into Cartoons using Python

Python文档阅读笔记-Turn Images into Cartoons using Python

Python文档阅读笔记-Turn Images into Cartoons using Python

IDEA插件系列（93）：Paste Images into Markdown插件——复制图片到markdown文件中

Translating Skills

Translating Virtual Machine Code