归并排序笔记

Posted 2022-08-18 Debroon

归并排序

• 原理
• • 算法策略：分治
  • 归并图示
  • 归并排序的微观模拟
  • 自底向上的归并排序
• 优化
• • 在有序数组上，变成 O(n) 算法
  • 加入插入排序
  • 内存操作优化
• 题目增益
• • 逆序对数量

 

---

原理

算法策略：分治

以冒泡排序为例，之所以慢，是因为每一次选出一个最大的数，都要和其它所有的数字相比，其实并不需要这么麻烦，要想提高效率，就要减少数据之间的相互比较。

最早对冒泡排序的改进是一种叫做归并排序的算法，它就利用了少做事情的思想，归并排序的思想大致如下：

• 冒泡排序：假如有一个学区，里面有 2 万名高中学生，如果让大家到一个超级大的学校上大课，再从中挑出学生中的尖子，效率一定高不了。这就相当于冒泡排序，每一个人都要和所有人去比。

• 归并排序：如果我们把 2 万人放到 10 所学校中，每所学校只有两千人，从各个学校先各自挑出学习尖子，再彼此进行比较，这就有效得多了。这就是归并排序原理。

• 快速排序：如果我们先划出几个分数线，根据个人成绩的高低把 2 万个学生分到十所学校去，第一所学校里的学生成绩最好，第十所最差，对比归并排序没有彼此比较的那步了，再找出学习尖子，那就容易了，工作量最小，这就是快速排序的原理。

其实归并、快排的设计思路，都是分治策略，分治是提高算法效率的一种思路。

把大问题分解为很多小问题，再逐个解决，再把小问题的解，合并成原来问题的解。

分治策略的用法在于，子问题的独立，子问题得到的答案是原问题的解。

 

---

归并图示

归并原理如下：

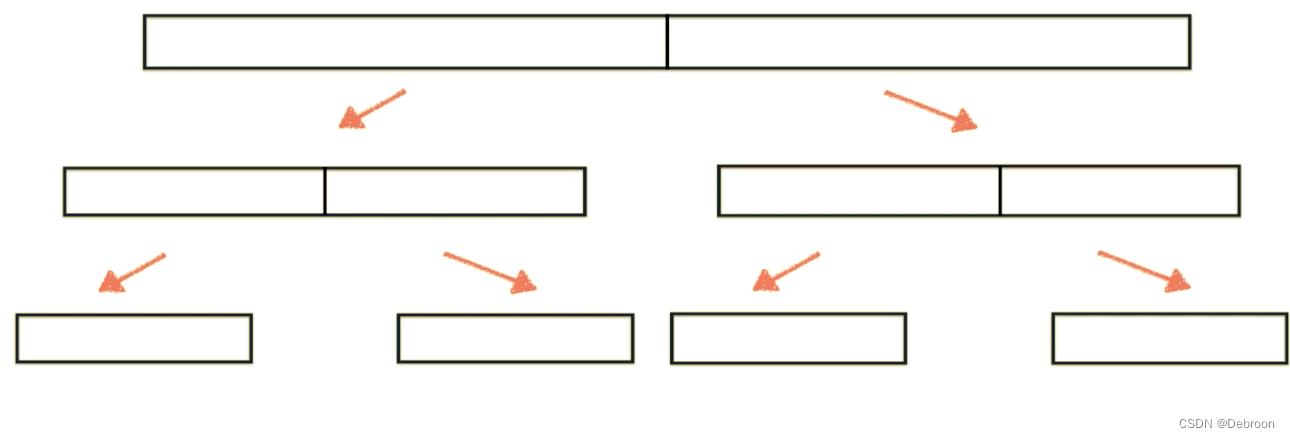
把全班同学分成两组，分别排序，那么从每一组中挑选出一个最大的，就能省去一半的相互比较时间。

于是他们就先将整个班级一分为二，先分别进行排序，再把两个排好序的组，合并成为一个有序的序列。相比排序，对有序的序列合并是很快的。归并排序这个词就是这么来的。

这样做大约可以节省一半时间。当然，节省一半时间意义不大，但是别着急，因为对一个班级分出来的两个小组，排序时也可以采用上述技巧。

第二步，就是对两个组的排序。显然我们不应该再用冒泡排序。既然能分成两组，就能把每个小组再分为两组，即分成四组，重复上面的算法，分别排序再合并。这样就能省 3/4 的时间。

再接下来，四组可以分为八组，能省 7/8 的时间，八组可以分为十六组，时间就不断省得越来越多。分到最后每个小组只剩下两个人的时候，其实就不用排序了，只要比较一次大小即可。

#include<iostream>
using namespace std;

/* 归并排序模板 */
void merge_sort(int a[], int l, int r)
    if( l >= r ) return;             // 最基本的问题：只有一个元素，或者没有元素，不用排序
    int mid = (l + r) / 2;           // 分界点
    merge_sort(a, l, mid);           // 分治，对前半部分排序
    merge_sort(a, mid+1, r);         // 分治，对后半部分排序
    
    int tmp[r - l + 1];              // 临时数组，存储排序好的值
    int i = l, j = mid+1, k = 0;     // 循环不变量 i、j，保证算法正确运行的关键，k只是一个计数变量
    /* 合并俩个有序数组 */
    while( i <= mid && j <= r)       // i, j 维护算法正确边界
        if(a[i] <= a[j]) tmp[k++] = a[i++];
        else tmp[k++] = a[j++];
    while( i <= mid ) tmp[k++] = a[i++];
    while( j <= r ) tmp[k++] = a[j++];
    for(i=l, j=0; i<=r; i++, j++) a[i] = tmp[j];  // 更新原数组，变成有序数组 


int main()
    int n, a[102400];
    cin >> n;
    for(int i=0; i<n; i++)
        cin >> a[i];
    merge_sort(a, 0, n-1);    
    for(int i=0; i<n; i++)
        cout << a[i] << ' ';

正确写出一个算法，定义清楚循环不变量是关键。

• 循环不变量初始化：需要几个，初始位置在哪里？
• 循环不变量范围：在哪个区间才能保证算法的正确性？

归并排序，分解过程是很简单的，就是一半一半的分。

void merge_sort(int a[], int l, int r)
    if( l >= r ) return;             // 最基本的问题：只有一个元素，或者没有元素，不用排序
    int mid = (l + r) / 2;           // 分界点
    merge_sort(a, l, mid);           // 分治，对前半部分排序
    merge_sort(a, mid+1, r);         // 分治，对后半部分排序

	/* 如何归并？*/
	merge(a, l, mid, r);             // 合并，对俩个有序数组排序

维护算法正确性的难点，在于归并过程。

归并过程转化为问题，即已知俩个有序的数组，如何合并为一个有序的数组？如：

• 数组一：1、3、5、6
• 数组二：2、4、7、8

因为是有序的，所以最小元素，要么是数组一中最小元素，要么是数组二中最小元素，所以只需要比较这俩个即可。

次最小、次次最小、···，都是如此，俩个数组中当前最小的那个。

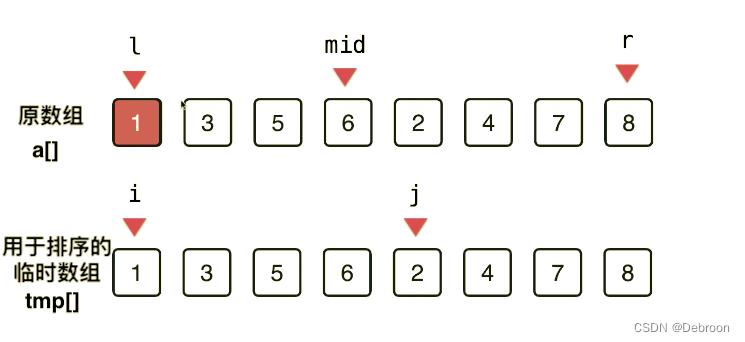
我们实现这个过程，需要定义俩个指针：

• 初始位置，在俩个数组的开头，$i=l，j=mid+1$

循环不变量 i, j 的范围是：

• 比较俩个元素 $a[i]<a[j]$，保存小的那个，a[i] 小：$tmp[k++]=a[i++]$，a[j] 小：$tmp[k++]=a[j++]$，之后这个指针向后移动一位。
• 直到指针到了数组最后一个元素后，这个数组排序完毕，即 $i=mid且j=r$。

 

---

归并排序的微观模拟

void merge_sort(int a[], int l, int r)
    if( l >= r ) return;             // 最基本的问题：只有一个元素，或者没有元素，不用排序
    int mid = (l + r) / 2;           // 分界点
    merge_sort(a, l, mid);           // 分治，对前半部分排序
    merge_sort(a, mid+1, r);         // 分治，对后半部分排序
    merge(a, l, mid, r);             // 合并，对俩个有序数组排序

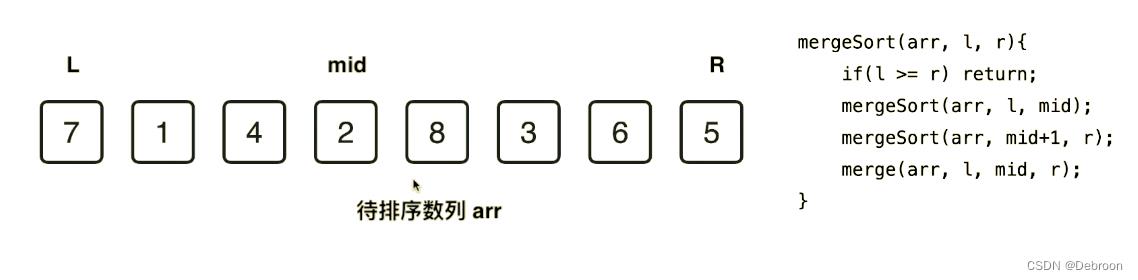
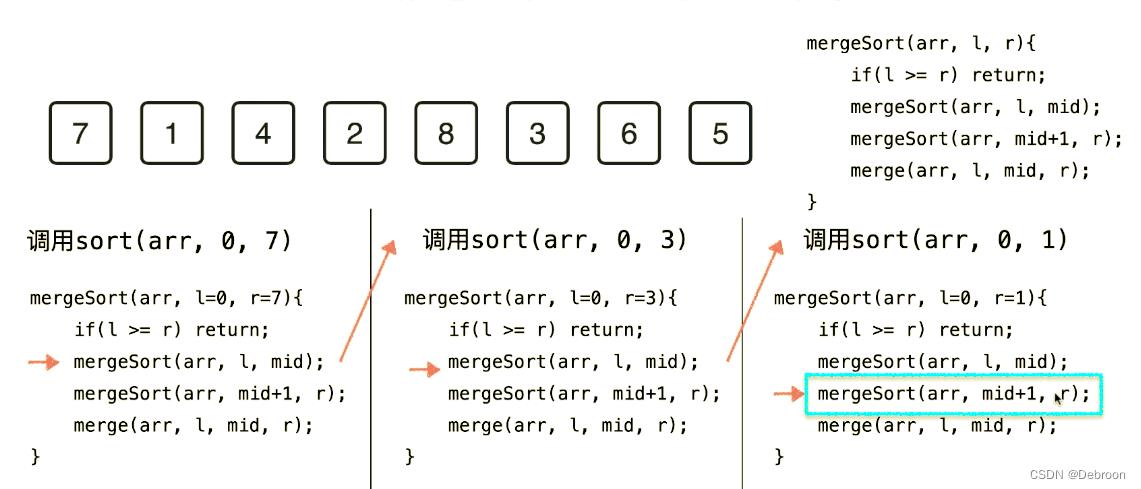
从调用 merge_sort(arr, 0, 7) 开始。

void merge_sort(int a[], int l=0, int r=7)
    if( l >= r ) return;             // 最基本的问题：只有一个元素，或者没有元素，不用排序
    int mid = (l + r) / 2;           // 分界点
    merge_sort(a, l, mid);           // 分治，对前半部分排序
    merge_sort(a, mid+1, r);         // 分治，对后半部分排序
    merge(a, l, mid, r);             // 合并，对俩个有序数组排序

因为 0 < 7，所以函数没有 return。
.
计算 mid = (0 + 7) / 2 = 3。
.
调用函数 merge_sort(a, 0, 3);
.

因为 0 < 3，所以函数没有 return。
.
计算 mid = (0 + 3) / 2 = 1。
.
调用函数 merge_sort(a, 0, 1);
.

因为 0 < 1，所以函数没有 return。
.
计算 mid = (0 + 1) / 2 = 0。
.
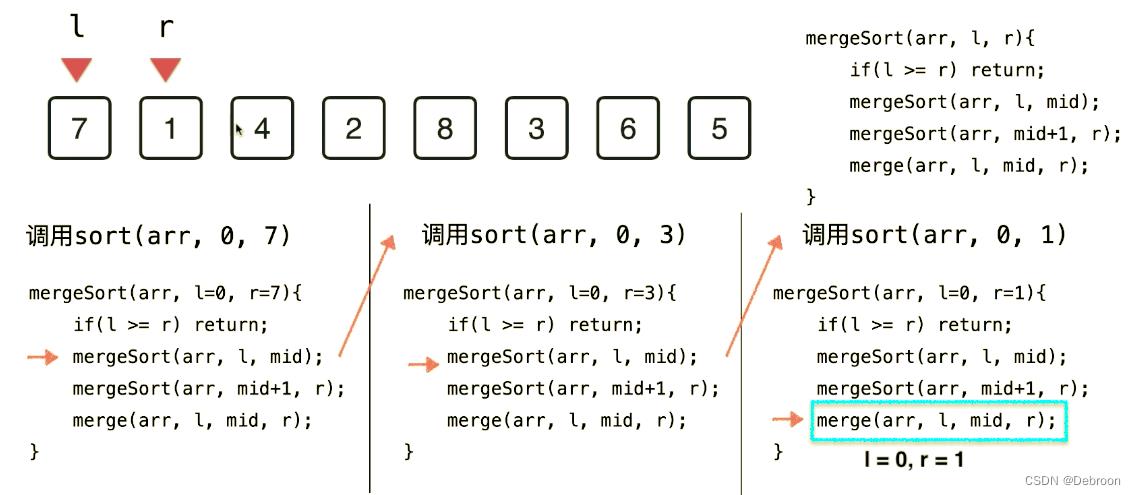
调用函数 merge_sort(a, 0, 0);
.

因为 0 == 0，函数 return;
.
merge_sort(a, 0, 0) 函数调用结束后，会回到 merge_sort(a, 0, 1) 上个调用函数的下一行
.
mid = 0, r = 1，调用 merge_sort(a, 1, 1)
.
因为 1 = 1，函数 return;
.
merge_sort(a, 1, 1) 函数调用结束后，会回到 merge_sort(a, 0, 1) 上个调用函数的下一行
.
merge(0, 1)
.
merge(0, 1)排序好后，变成 1、7、4、2、8、3、6、5
.
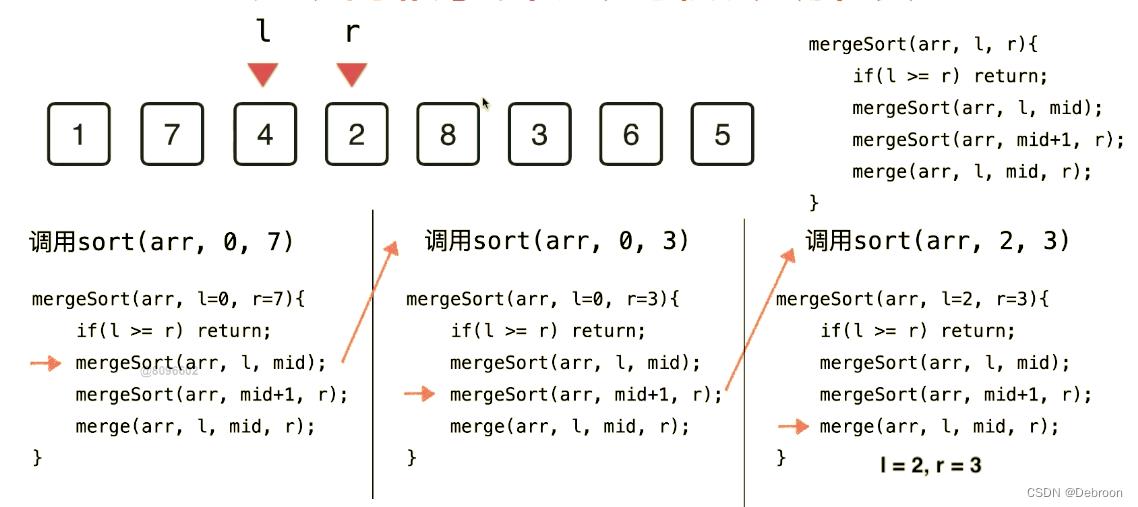
merge_sort(a, 0, 1) 函数结束后，会回到 merge_sort(a, 0, 3) 上个调用函数的下一行，merge_sort(a, 2, 3)
.
merge(2, 3) 排序好后，变成 1、7、2、4、8、3、6、5
.
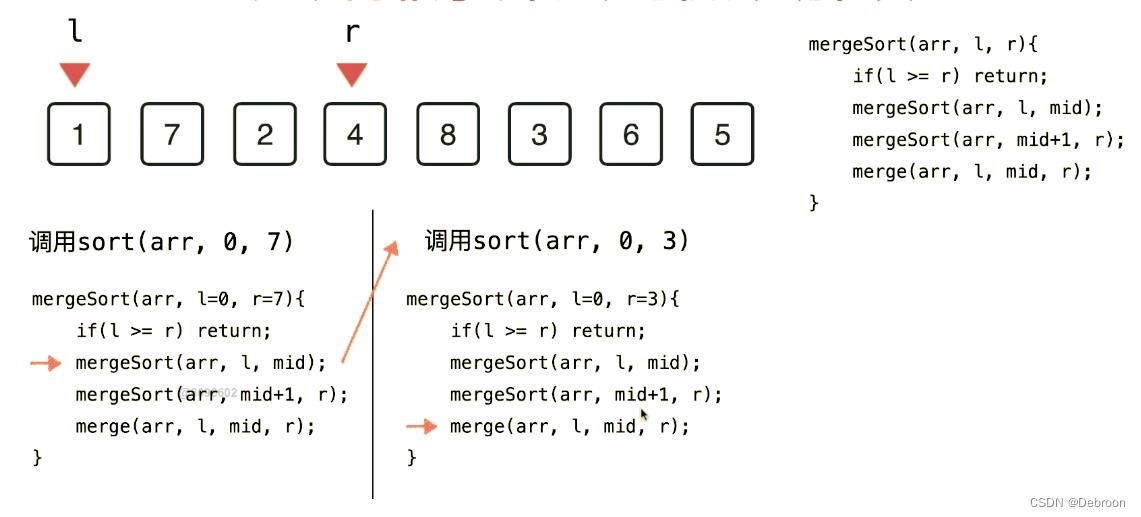
merge_sort(a, 2, 3) 函数结束后，会回到 merge_sort(a, 0, 3) 上个调用函数的下一行，merge(0, 3)
.

1、7 有序，2、4 有序，此时合并俩个有序数组，变成 1、2、4、7、8、3、6、5
.
至此，原数组 a[] 左半部分排序完毕，右半部分以此类推。

归并排序的时间复杂度：$O(nlogn)$，空间复杂度：$O(n)$。
 

---

自底向上的归并排序

递归版本是自顶向下的，归并排序也可以自底向上实现。

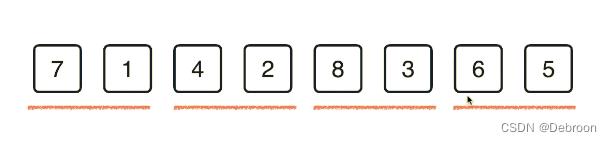
首先把数列俩俩分，排好序后，再四四分：

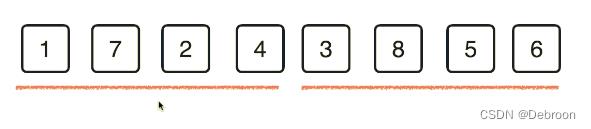
排好序后，再八八分，翻倍涨：

void merge_sort(int a[], int l, int r)
	for( int i=1; i<r; i += i )	// 循环不变量 i：1、2、4、8 ···· < n
		for( int j=0; j+i<r; j += 2*i ) // 合并俩个数组 [j, j+i-1] [j+i, j+i+i-1]
			merge(a, j, j+i-1, min(j+i+i-1, r-1));

 

---

优化

 

---

在有序数组上，变成 O(n) 算法

后面还有人优化了归并排序，优化的地方是充分利用待排序数据列，很多序列是已经排好序的不需要再重新排序，利用这个特性并且加上合适的合并规则可以更加高效的排序剩下的待排序序列。

void merge_sort(int a[], int l=0, int r=7)
    if( l >= r ) return;             // 最基本的问题：只有一个元素，或者没有元素，不用排序
    int mid = (l + r) / 2;           // 分界点
    merge_sort(a, l, mid);           // 分治，对前半部分排序
    merge_sort(a, mid+1, r);         // 分治，对后半部分排序
    if ( a[mid] > a[mid+1] )         // 优化，如果数组有序，不需要合并
    	merge(a, l, mid, r);         // 合并，对俩个有序数组排序

 

---

加入插入排序

小规模的数据规模，插入排序比归并快。

void merge_sort(int a[], int l=0, int r=7)
    if( r - l <= 15 ) 
    	insert_sort(a, l, r), return;
    int mid = (l + r) / 2;           // 分界点
    merge_sort(a, l, mid);           // 分治，对前半部分排序
    merge_sort(a, mid+1, r);         // 分治，对后半部分排序
    if ( a[mid] > a[mid+1] )         // 优化，如果数组有序，不需要合并
    	merge(a, l, mid, r);         // 合并，对俩个有序数组排序

 

---

内存操作优化

我们在递归函数内部申请数组空间 tmp，这个过程会持续很多次，我们可以只开创一次。

void merge_sort(int a[], int l=0, int r=7, int tmp[])
    if( l <= r ) 
    	return;
    int mid = (l + r) / 2;           // 分界点
    merge_sort(a, l, mid);           // 分治，对前半部分排序
    merge_sort(a, mid+1, r);         // 分治，对后半部分排序
    if ( a[mid] > a[mid+1] )         // 优化，如果数组有序，不需要合并
    	merge(a, l, mid, r, tmp);    // 合并，对俩个有序数组排序

还有一种可以让空间复杂度变成 $O(1)$，原地归并排序。
 

---

题目增益

 

---

逆序对数量

题目链接：https://leetcode.cn/problems/shu-zu-zhong-de-ni-xu-dui-lcof/

最朴素的想法，双指针遍历比较，时间复杂度 $O(n^2)$：

int ans = 0;
for(int i=0; i<n; i++)
	for(int j=i+1; j<n; j++)
		if(a[i] > a[j])	ans ++;

其实我们可以用归并排序快速求解逆序对问题。

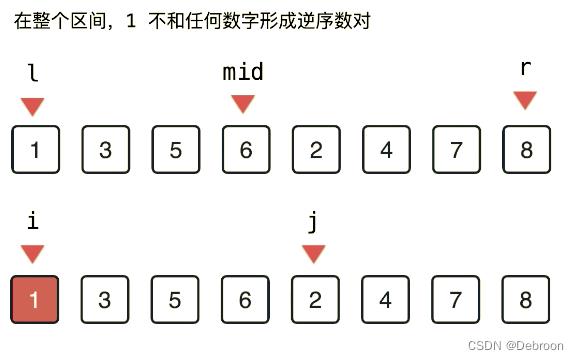
因为 1 在左边区间，左边没有元素，或者已经归并完了，所以没有逆序对。

i++

由于 2 在右边区间，左边还没归并的元素，就形成了逆序对。

因为 3 在左边区间，前面的元素归并完了，右边数组的元素由于在 3 后面，所以也没有形成逆序对。

i++

由于 4 在右边区间，左边还没归并的元素，就形成了逆序对。

直到 i = mid+1, j > r，结束。

规律：在归并过程中，如果后面区间的元素归并上来，就会和左边区间剩余元素形成逆序数对。

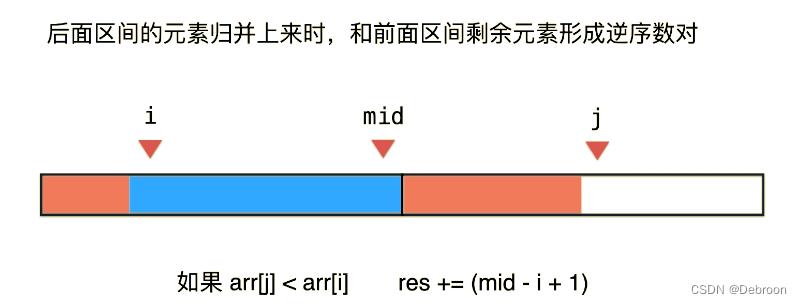
#include<iostream>
using namespace std;
long long ans;

void merge_sort(int a[], int l, int r)
    if( l>=r) return;
    int mid = (l+r)/2;
    merge_sort(a, l, mid);
    merge_sort(a, mid+1, r);
    
    int tmp[r-l+1];
    int i = l, j = mid+1, k = 0;
    while( i <= mid && j <= r)
        if(a[i] <= a[j]) tmp[k++] = a[i++];
        else tmp[k++] = a[j++], ans += mid - i + 1;  // 记录
    while(i<=mid) tmp[k++] = a[i++];
    while(j<=r) tmp[k++] = a[j++];
    for(i=l, j=0; i<=r; i++, j++) a[i] = tmp[j];


int main()
    int n, a[102400];
    cin >> n;
    for(int i=0; i<n; i++)
        cin >> a[i];
    merge_sort(a, 0, n-1);
    cout << ans;