2022国赛数学建模思路 - 案例：K近邻算法

Posted 2022-08-15 建模君A

2022 高教社杯(国赛数学建模)思路解析

2022高教社杯ABCD赛题思路解析：

https://blog.csdn.net/dc_sinor/article/details/126211983

K近邻算法

我们先看一张图：

观察一下，黄点和蓝点代表了两种标签，比如每个蓝点都是一个合格的产品，黄点是劣质的产品。事实上在图中可以看到，相同标记的样本点通常是成团的形式聚在一起，因为合格的产品在属性上一定是相同或相似的（合格的产品在属性上不太可能会跑到不合格的一类中去）。

那么我们预测过程中，查看被预测的样本x是属于哪一堆来判断它是黄豆还是蓝豆是不是可行呢？

当然可以啦，K近邻就是一种基于该原理的算法。从名字里就可以看到，K近邻样本的预测上，是看被预测样本x离哪一团最近，那它就是属于哪一类的。

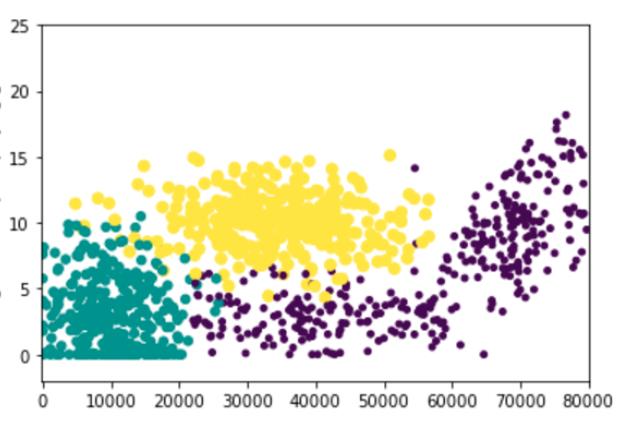
图里有两种标记，就叫它黄豆、绿豆、紫豆好了（这里也能看到，K近邻不像感知机只能划分两种类，K近邻是一种多类划分的模型）。当我们要预测一个样本x时，将x的特征转换为在图中的坐标点，分别计算和绿豆、黄豆、紫豆的举例，比如说距离分别为1， 1.5， 0.8。选择其中距离最小的紫豆作为样本x的预测类别。

那啥是样本x和一团豆的距离？
1.找到样本x最近的点，该点的类就是样本的预测类：这是一种方法，但是如果有噪音呢（同一块区域又有黄点又有绿点）？比如说x实际上是黄豆，但是它的位置在黄豆和绿豆的边界上（例如上图黄点和绿点的交叉处），很可能它最近的点是一个绿点，所以….不太好

2.与每一团的中心点进行距离计算：分别计算绿色、黄色、紫色的中心点，判断距离最小的类即为预测输出类。这样会不会有问题吗？我们看一下上图中绿色和紫色交叉的地方，很明显在这个交叉位置离绿色很近，与紫色中心点较远，但实际上紫色的。所以……不太好

3.找到样本点周围的K个点，其中占数目最多的类即预测输出的类：克服了前两种方法的弊端，实际上这就是K近邻所使用的算法

knn数学原理

K近邻并没有显式的学习过程，也就是不需要对训练集进行学习。预测过程中直接遍历预测点与所有点的距离，并找到最近的K个点即可。找到K个最近点后，使用多数表决（即投票）的方式确定预测点的类别。式3.1I(yi=ci)中的I为指示函数，当括号内条件为真时I(true)=1，I(false)=0。argmax表示令后式数值最大时的参数，例如argmax(-X^2 + 1)的结果为0，因为x=0时-X^2 + 1结果为1，为最大值。

式3.1表示对于每一个类Cj，进行I(yi=cj)进行求和，就是计算这K个点中有多少个标记为Cj的点，例如K=25，一共有四个类分别为C1、C2、C3、C4，25个点中他们的个数分别有10、5、1、9个，那么最多数目的类别C1就是样本点的预测类别。

距离度量

在多维空间中有很多种方式可以计算点与点之间的举例，通常采用欧氏距离作为K近邻的度量单位（大部分模型中欧氏距离都是一种不错的选择）。其实就是样本A、B中每一个特征都互相相减，再平方、再求和。与二维中两点之间距离计算方式相同，只是扩展到了多维。

曼哈顿与P=无穷可以不用深究，在本文中使用曼哈顿准确度极差（仅针对Mnist数据集使用K近邻的情况），这两种方式目前仅作了解即可。

KNN的缺点

1、在预测样本类别时，待预测样本需要与训练集中所有样本计算距离，当训练集数量过高时（例如Mnsit训练集有60000个样本），每预测一个样本都要计算60000个距离，计算代价过高，尤其当测试集数目也较大时（Mnist测试集有10000个）。

1、K近邻在高维情况下时（高维在机器学习中并不少见），待预测样本需要与依次与所有样本求距离。向量维度过高时使得欧式距离的计算变得不太迅速了。本文在60000训练集的情况下，将10000个测试集缩减为200个，整个过程仍然需要308秒（曼哈顿距离为246秒，但准确度大幅下降）。

使用欧氏距离还是曼哈顿距离，性能上的差别相对来说不是很大，说明欧式距离并不是制约计算速度的主要方式。最主要的是训练集的大小，每次预测都需要与60000个样本进行比对，同时选出距离最近的K项。

代码实现

import numpy as np
import time
def loadData(fileName):
    '''
    加载文件
    :param fileName:要加载的文件路径
    :return: 数据集和标签集
    '''
    print('start read file')
    #存放数据及标记
    dataArr = []; labelArr = []
    #读取文件
    fr = open(fileName)
    #遍历文件中的每一行
    for line in fr.readlines():
        #获取当前行，并按“，”切割成字段放入列表中
        #strip：去掉每行字符串首尾指定的字符（默认空格或换行符）
        #split：按照指定的字符将字符串切割成每个字段，返回列表形式
        curLine = line.strip().split(',')
        #将每行中除标记外的数据放入数据集中（curLine[0]为标记信息）
        #在放入的同时将原先字符串形式的数据转换为整型
        dataArr.append([int(num) for num in curLine[1:]])
        #将标记信息放入标记集中
        #放入的同时将标记转换为整型
        labelArr.append(int(curLine[0]))
    #返回数据集和标记
    return dataArr, labelArr
def calcDist(x1, x2):
    '''
    计算两个样本点向量之间的距离
    使用的是欧氏距离，即 样本点每个元素相减的平方  再求和  再开方
    欧式举例公式这里不方便写，可以百度或谷歌欧式距离（也称欧几里得距离）
    :param x1:向量1
    :param x2:向量2
    :return:向量之间的欧式距离
    '''
    return np.sqrt(np.sum(np.square(x1 - x2)))
    #马哈顿距离计算公式
    # return np.sum(x1 - x2)
def getClosest(trainDataMat, trainLabelMat, x, topK):
    '''
    预测样本x的标记。
    获取方式通过找到与样本x最近的topK个点，并查看它们的标签。
    查找里面占某类标签最多的那类标签
    （书中3.1 3.2节）
    :param trainDataMat:训练集数据集
    :param trainLabelMat:训练集标签集
    :param x:要预测的样本x
    :param topK:选择参考最邻近样本的数目（样本数目的选择关系到正确率，详看3.2.3 K值的选择）
    :return:预测的标记
    '''
    #建立一个存放向量x与每个训练集中样本距离的列表
    #列表的长度为训练集的长度，distList[i]表示x与训练集中第
    ## i个样本的距离
    distList = [0] * len(trainLabelMat)
    #遍历训练集中所有的样本点，计算与x的距离
    for i in range(len(trainDataMat)):
        #获取训练集中当前样本的向量
        x1 = trainDataMat[i]
        #计算向量x与训练集样本x的距离
        curDist = calcDist(x1, x)
        #将距离放入对应的列表位置中
        distList[i] = curDist
    #对距离列表进行排序
    #argsort：函数将数组的值从小到大排序后，并按照其相对应的索引值输出
    #例如：
    #   >>> x = np.array([3, 1, 2])
    #   >>> np.argsort(x)
    #   array([1, 2, 0])
    #返回的是列表中从小到大的元素索引值，对于我们这种需要查找最小距离的情况来说很合适
    #array返回的是整个索引值列表，我们通过[:topK]取列表中前topL个放入list中。
    #----------------优化点-------------------
    #由于我们只取topK小的元素索引值，所以其实不需要对整个列表进行排序，而argsort是对整个
    #列表进行排序的，存在时间上的浪费。字典有现成的方法可以只排序top大或top小，可以自行查阅
    #对代码进行稍稍修改即可
    #这里没有对其进行优化主要原因是KNN的时间耗费大头在计算向量与向量之间的距离上，由于向量高维
    #所以计算时间需要很长，所以如果要提升时间，在这里优化的意义不大。（当然不是说就可以不优化了，
    #主要是我太懒了）
    topKList = np.argsort(np.array(distList))[:topK]        #升序排序
    #建立一个长度时的列表，用于选择数量最多的标记
    #3.2.4提到了分类决策使用的是投票表决，topK个标记每人有一票，在数组中每个标记代表的位置中投入
    #自己对应的地方，随后进行唱票选择最高票的标记
    labelList = [0] * 10
    #对topK个索引进行遍历
    for index in topKList:
        #trainLabelMat[index]：在训练集标签中寻找topK元素索引对应的标记
        #int(trainLabelMat[index])：将标记转换为int（实际上已经是int了，但是不int的话，报错）
        #labelList[int(trainLabelMat[index])]：找到标记在labelList中对应的位置
        #最后加1，表示投了一票
        labelList[int(trainLabelMat[index])] += 1
    #max(labelList)：找到选票箱中票数最多的票数值
    #labelList.index(max(labelList))：再根据最大值在列表中找到该值对应的索引，等同于预测的标记
    return labelList.index(max(labelList))
def test(trainDataArr, trainLabelArr, testDataArr, testLabelArr, topK):
    '''
    测试正确率
    :param trainDataArr:训练集数据集
    :param trainLabelArr: 训练集标记
    :param testDataArr: 测试集数据集
    :param testLabelArr: 测试集标记
    :param topK: 选择多少个邻近点参考
    :return: 正确率
    '''
    print('start test')
    #将所有列表转换为矩阵形式，方便运算
    trainDataMat = np.mat(trainDataArr); trainLabelMat = np.mat(trainLabelArr).T
    testDataMat = np.mat(testDataArr); testLabelMat = np.mat(testLabelArr).T
    #错误值技术
    errorCnt = 0
    #遍历测试集，对每个测试集样本进行测试
    #由于计算向量与向量之间的时间耗费太大，测试集有6000个样本，所以这里人为改成了
    #测试200个样本点，如果要全跑，将行注释取消，再下一行for注释即可，同时下面的print
    #和return也要相应的更换注释行
    # for i in range(len(testDataMat)):
    for i in range(200):
        # print('test %d:%d'%(i, len(trainDataArr)))
        print('test %d:%d' % (i, 200))
        #读取测试集当前测试样本的向量
        x = testDataMat[i]
        #获取预测的标记
        y = getClosest(trainDataMat, trainLabelMat, x, topK)
        #如果预测标记与实际标记不符，错误值计数加1
        if y != testLabelMat[i]: errorCnt += 1
    #返回正确率
    # return 1 - (errorCnt / len(testDataMat))
    return 1 - (errorCnt / 200)
if __name__ == "__main__":
    start = time.time()
    #获取训练集
    trainDataArr, trainLabelArr = loadData('../Mnist/mnist_train.csv')
    #获取测试集
    testDataArr, testLabelArr = loadData('../Mnist/mnist_test.csv')
    #计算测试集正确率
    accur = test(trainDataArr, trainLabelArr, testDataArr, testLabelArr, 25)
    #打印正确率
    print('accur is:%d'%(accur * 100), '%')
    end = time.time()
    #显示花费时间
print('time span:', end - start)

2022 高教社杯(国赛数学建模)思路解析

2022高教社杯ABCD赛题思路解析：

https://blog.csdn.net/dc_sinor/article/details/126211983