深度学习100问之深入理解Vanishing/Exploding Gradient（梯度消失/爆炸）

Posted 2022-08-13 我是管小亮

这几天正在看梯度消失/爆炸，在深度学习的理论中梯度消失/爆炸也是极其重要的，所以就抽出一段时间认真地研究了一下梯度消失/爆炸的原理，以下为参考网上的几篇文章总结得出的。

本文分为四个部分：第一部分主要介绍深度学习中一些关于梯度消失/爆炸(Vanishing/Exploding Gradient)的基础。第二部分主要介绍深度学习中什么是梯度消失/爆炸；第三部分主要介绍怎么解决梯度消失/爆炸。

一、Preface

本文主要深度理解在深度学习中的梯度消失/爆炸以及解决方案。

随着神经网络层数的增加，会出现梯度消失/爆炸(Vanishing/Exploding Gradient)的问题，在介绍详细的内容之前，先简单说一说梯度问题的根源——深度神经网络和反向传播。

在目前的深度学习研究中，深度学习的神经网络的发展造就了一种可能：我们可以搭建更深层的网络，完成很复杂的任务，VGG这个论文就是主要提出并证明了深度对于深度学习神经网络性能的提升。除此之外，LSTM等的最终结果也表明了在处理复杂任务上，深层网络比浅层网络具有更好的性能。

但是，我们说目前优化神经网络的方法都是基于反向传播的思想，即根据损失函数计算的误差通过链式法则、梯度下降、反向传播的方式，更新和优化深度学习神经网络中的权值。这么做最大的原因便是基于非线性激活函数对于网络的作用，整个深度网络都可以看做是一个复合非线性函数。

$$F(x)=f_n(...f_3(f_2(f_1(x)\ast W_1+b_1)\ast W_2+b_2)\ast W_3+b_3)...)$$

我们希望深度学习可以很好的完成输入到输出之间的映射通过上面的这个多元函数。假设对于不同的输入，输出的最优解是$g(x)$，那么，优化网络的目的就是找到合适的权值，让损失函数更小，比如最简单的损失函数：
$$Loss=||g(x)-f(x)|{|}_2^2$$

如果损失函数的数据空间是下图这样的，我们寻找最优的权值就是为了寻找下图中的最小值点，对于这种数学寻找最小值问题，目前最主流的方法就是梯度下降法。

二、Why、What

梯度消失与梯度爆炸其实是一种情况，那么为什么会出现这两种情况？

为什么会出现梯度消失的现象呢？因为在深层网络中通常采用的激活函数是$sigmoid$，在该函数中最小值和最大值的梯度(也就是倒数)都趋近于0。神经网络的反向传播是逐层对函数偏导相乘，当神经网络层数非常深的时候，最后一层产生的偏差就因为乘了很多的小于1的数而越来越小，最终就会变为0，从而导致层数比较浅的权重没有更新。

那么什么是梯度爆炸呢？梯度爆炸就是在深层网络中由于初始化权值过大，前面层会比后面层变化的更快，就会导致权值越来越大，梯度爆炸的现象就发生了。

图中是一个四层的全连接网络，根据公式：

$$F(x)=f_n(...f_3(f_2(f_1(x)\ast W_1+b_1)\ast W_2+b_2)\ast W_3+b_3)...)$$

我们可以得到(n+1)层的输入，也就是n层的输出的关系，f是激活函数，

$$f_{n+1}(x)=f(f_n(x)\ast W_{n+1}+b_{n+1})$$

如果要更新第 i 隐藏层的权值信息，根据链式求导法则，更新梯度信息：

$$\Delta W_i=\frac{\partial Loss}{\partial W_i}=\frac{\partial Loss}{\partial f_4(x)}\frac{\partial f_4(x)}{\partial f_3(x)}\frac{\partial f_3(x)}{\partial f_i(x)}\frac{\partial f_i(x)}{\partial W_i}$$

所以说$\frac{\partial f_4(x)}{\partial f_3(x)}$就是对激活函数的求导，如果$\frac{\partial f_4(x)}{\partial f_3(x)}$大于1，那么层数增多的时候，乘以一个大于1的数会变得更大，最终的求出的梯度更新将以指数形式增加，即发生梯度爆；如果$\frac{\partial f_4(x)}{\partial f_3(x)}$小于1，那么随着层数增多，乘以一个小于1的数会变得更小，求出的梯度更新信息将会以指数形式衰减，即发生了梯度消失。

例如：1)大于1时，$1.2^5=2.48832$；2)小于1时，$0.8^5=0.32768$。这两个例子是比较直观的数学理解方式了。

下面来看几组通过增加隐藏层层数后的每一层偏置的变化情况(从数学角度上在这里可以理解为在反向传播过程中每一次迭代对每一层偏置的求导结果变化情况，也就是梯度的大小变化情况，也就是需要更新的值的大小变化情况)：



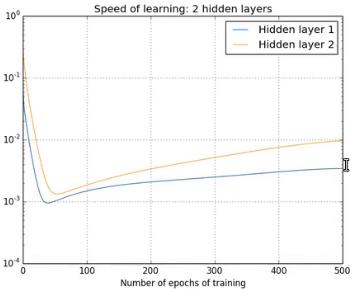
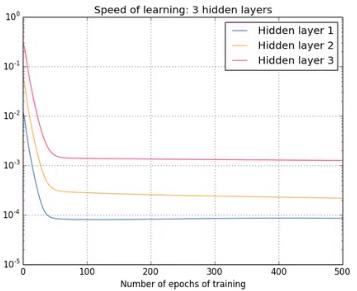
可以看出，第一个隐藏层比第四个几乎要慢100倍，这就是梯度消失，如果内层的梯度比外层大很多，就叫做梯度爆炸。

这么看来，梯度消失/爆炸(Vanis