基于GA优化算法的磁性贴片位置布置优化算法matlab仿真

Posted 2022-08-12 fpga和matlab

目录

一、理论基础

二、案例背景

1.问题描述

2.思路流程

三、部分MATLAB仿真

四、仿真结论分析

五、参考文献

---

一、理论基础

二、案例背景

1.问题描述

2.思路流程

首先来分析一下这个最优计算公式：

 

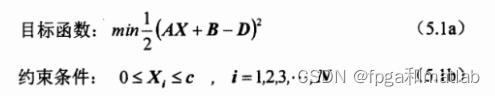
一、A矩阵为对圆筒内表面上的132个点进行贴片，进而对匀场球体表面上132个测量点的贡献矩阵系数。 以上数据构成MATLAB大数据矩阵，其中大矩阵中的数据按照从-5至+5的顺序进行周期排列填充，其中行数为12*11=132行。           

        其中12为重复的周期数，11为每个周期中所含有的行数=-5至+5,一共为11行，每行中的元素按照表格中的角度从小到大进行填充，          

        每个角度中的列数据按照由上至下的顺序填充，每行中含有的数据为11*12=132个数据，也即构成大矩阵的132列。所以，大

        矩阵中一共含有的填充数据位（12*11）（总行数）*132（总列数）=17424个数据。（此矩阵也即算法中的贡献因子矩阵A）

二、每个位置上的贴片数量构成的矩阵X，贴片位置数一共为12*11=132个，其中12代表沿着圆筒圆周方向将360°等分12份，11代表每一等分位置处，沿着轴向位置从坐标-5至+5的11个位置（即11个位置处的贴片数量可表示为：-x5、-x4、-x3、-x2、-x1、x0、+x1、+x2、+x3、+x4、+x5），所以矩阵X中的元素数为12*11=132个，可表示成132*1的矩阵。

三、B矩阵为初始磁场分布数值列矩阵（需要填充的数据详见上表-1）

四、D矩阵为目标磁场分布数值列矩阵（需要填充的数据详见上表-3），各点目标场值的偏差量控制在-2000Hz～2000Hz。

三、部分MATLAB仿真

clc;
clear;
close all;
warning off;
addpath 'GA_toolbox\\'
%初始矩阵读取
[Ini_c,B,B0,D,D0,A0,A1,A2,A3,A4,A5,A6,A7,A8,A_1,A_2,A_3,A_4,A_5,A_6,A_7,A_8]=func_ini_matrix();
 

%获得A,插值，变为相同维度
A8   = A8.*[B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0];
A7   = A7.*[B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0];
A6   = A6.*[B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0];
A5   = A5.*[B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0];
A4   = A4.*[B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0];
A3   = A3.*[B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0];
A2   = A2.*[B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0];
A1   = A1.*[B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0];
A0   = A0.*[B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0];
A_1  = A_1.*[B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0];
A_2  = A_2.*[B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0];
A_3  = A_3.*[B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0];
A_4  = A_4.*[B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0];
A_5  = A_5.*[B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0];
A_6  = A_6.*[B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0];
A_7  = A_7.*[B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0];
A_8  = A_8.*[B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0];

A     = [A_8,A_7,A_6,A_5,A_4,A_3,A_2,A_1,A0,A1,A2,A3,A4,A5,A6,A7,A8];
Ax    = [A;A;A;A;A;A;A;A;A;A;A;A];  %这个位置就是之前说的数据A太小导致 
 

Ax    = imresize(Ax,[132,132]);
 
 
[R,C] = size(B);
%[-x5、-x4、-x3、-x2、-x1、x0、+x1、+x2、+x3、+x4、+x5]'
X     = zeros(R*C,1);
%矩阵预先处理，即维度变换
B     = B/1e6+[B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0];
D     = D/1e6+[D0,D0,D0,D0,D0,D0,D0,D0,D0,D0,D0,D0];

Bx    = reshape(B,[R*C,1]);
Dx    = reshape(D,[R*C,1]);

%约束条件
Cmax  = 20;

%下面开始使用遗传优化算法
%根据遗传算法进行参数的拟合
MAXGEN = 500;
NIND   = 1000;
Nums   = length(Dx);

Chrom  = crtbp(NIND,Nums*10);
Sm     = 0;
Areas  = [];

for i = 1:Nums
    Areas = [Areas,[0;Cmax]];
end
 
FieldD = [rep([10],[1,Nums]);Areas;rep([0;0;0;0],[1,Nums])];
 
gen   = 0;
for a=1:1:NIND 
 
    %计算对应的目标值
    Xx             = round(Cmax*rand(1,Nums));
    [epls]         = func_obj(Ax,Xx,Bx,Dx);
    E              = epls;
    Js(a,1)        = E;
end

Objv  = (Js+eps);
gen   = 0; 
 
ERR=zeros(1,MAXGEN);

while gen < MAXGEN;   
      gen
      Pe0 = 0.995;
      pe1 = 0.005; 
      FitnV=ranking(Objv);    
      Selch=select('sus',Chrom,FitnV);    
      Selch=recombin('xovsp', Selch,Pe0);   
      Selch=mut( Selch,pe1);   
      phen1=bs2rv(Selch,FieldD);   
 
      for a=1:1:NIND  
          Xx             = phen1(a,:);
          for jj = 1:Nums
              if Xx(jj) < 1 
                 Xx(jj) = 0;
              end
              if Xx(jj) > Cmax 
                 Xx(jj) = Cmax;
              end
          end
          Xx             = round(Xx);
          %计算对应的目标值
          epls           = func_obj(Ax,Xx,Bx,Dx);
          E              = epls;
          JJ(a,1)        = E;
          Xx2a         = Xx;
      end 
      Objvsel=(JJ);    
      [Chrom,Objv]=reins(Chrom,Selch,1,1,Objv,Objvsel);   
      gen=gen+1; 
      %保存参数收敛过程和误差收敛过程以及函数值拟合结论
      index1     = isnan(JJ);
      index2     = find(index1 == 1);
      JJ(index2) = [];
      ERR(gen)=mean(JJ);
end 

figure;plot(ERR)
xlabel('优化迭代次数');
ylabel('误差（Mhz）');
grid on

[V,I]   = min(JJ);
Xx_best = Xx2I;


X       = reshape(Xx_best,[11,12]) 


y       = Ax*Xx_best'+Bx;
Y       = (reshape(y,[11,12]) - ([B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0,B0]));

round(1e6*max(max(Y)))
 
 
 

四、仿真结论分析

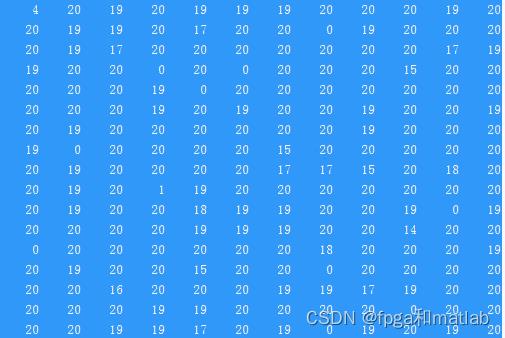
优化后的X位置信息

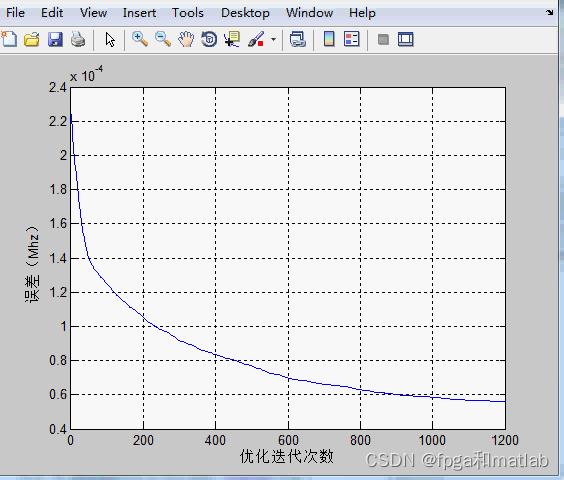
GA优化迭代过程。

五、参考文献

[1]董健腾, 龙绪明, 曹宏耀,等. 贴片机贴装路径优化的改进遗传算法[J]. 电子工业专用设备, 2015(12):6.A10-45