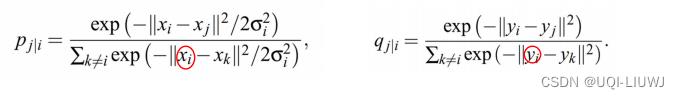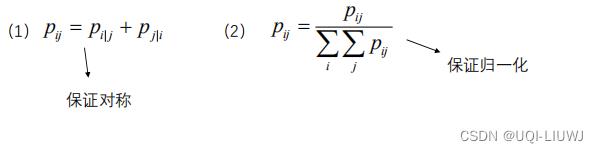机器学习笔记：t-SNE

Posted 2022-08-11 UQI-LIUWJ

0 前言

• t-SNE（t-Distributed Stochastic Neighbor Embedding）
• 是一种非常常用的数据降维，常用于数据可视化
• t-SNE/SNE的基本原理是：
  • 在高维空间构建一个概率分布拟合高维样本点间的相对位置关系
  • 在低维空间，也构建 一个概率分布，拟合低维样本点之间的位置关系
  • 通过学习，调整低维数据点， 令两个分布接近

1 SNE 随机邻域嵌入 （ Stochastic Neighbor Embedding ）

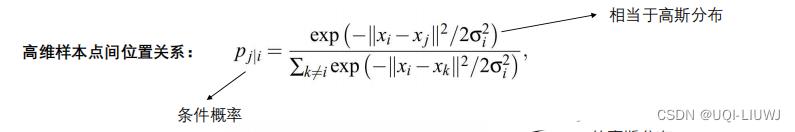
 （类似于softmax）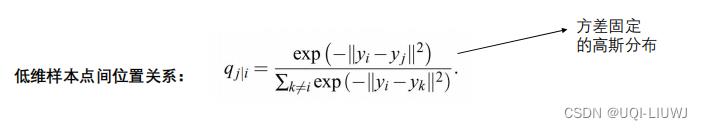

 

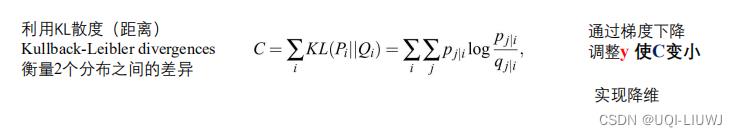
• 如果低维映射点yi和yj成功正确地建模了高维数据点xi和xj之间的相似性，则条件概率pj|i和qj|i将相等。

• 受这一观察结果的启发，SNE的目标是找到一种低维数据表示法，以最小化pj|i和qj|i之间的分布距离（两个条件分布接近）

1.1 SNE主要缺点

1.1.1 距离不对称

不难发现是不等的（分母不一样） ，这就导致了i—>j和j—>i的距离不对称。【与实际情况不符】

改进的方法是使用联合概率而不是条件概率

        在实际问题中，计算所有的需要太多的计算复杂度，于是实际应用中，一般是：

• 

 1.1.2 拥挤体现

        从高维到低维进行转换的过程中，低维点的距离无法建模高维点之间的位置关系，使得高维空间中距离较大的点对，在低维空间距离会变得较小         比如原来红绿点之间距离很远，降维之后距离就很近了

解决方法  利用拖尾较大的 student-t分布 来对低维点建模

 

 

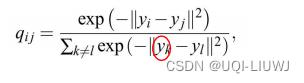
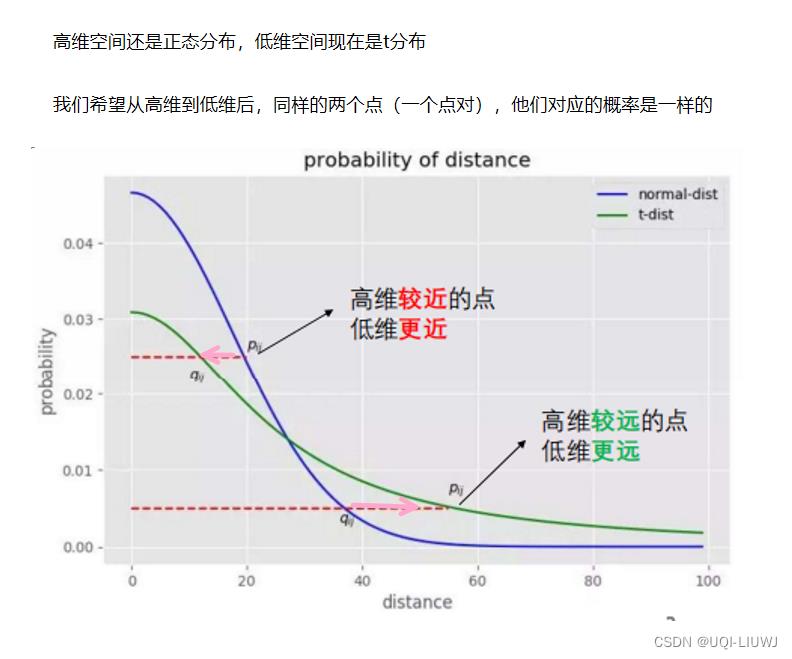
 2 T-SNE

2.1 σ的求法

最naive的方法就是随机设置了。 

更有效地方法如下：

我们把

 

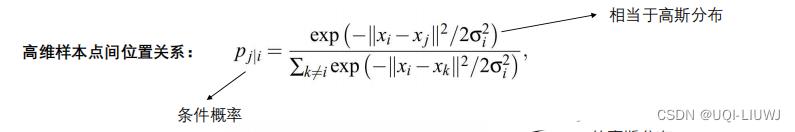
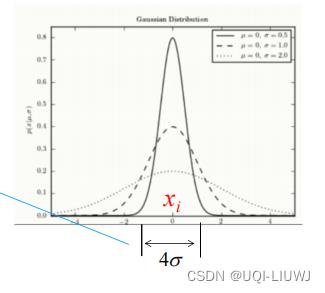
看成高斯分布，那么σ就类似于标准差

根据高斯分布的性质，我们知道，在(k是一个常数）的区间内，概率是比较大的。

所以我们根据xi周围临近点的数量，来增减σ

那么，如何对σ进行定量的约束呢，我们设置一个固定的参数perlexity，表示分布的熵。

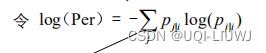
其中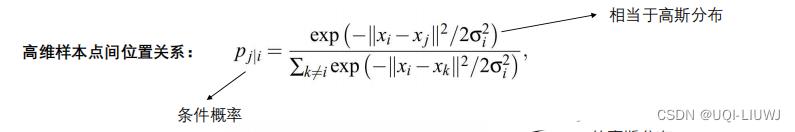

不难发现熵（perplexity）和σi成正比，所以我们可用类似于二分查找法来确定σi