sklearn笔记：PCA

Posted 2022-08-09 UQI-LIUWJ

0 理论知识

机器学习笔记PCA_UQI-LIUWJ的博客-CSDN博客

1 基本使用方法

class sklearn.decomposition.PCA(
    n_components=None, 
    *, 
    copy=True, 
    whiten=False, 
    svd_solver='auto', 
    tol=0.0, 
    iterated_power='auto', 
    n_oversamples=10, 
    power_iteration_normalizer='auto', 
    random_state=None)

2 参数说明

n_components	降至几维【特征的数量】（如果n_components没有配置的话，保持维度）
whiten	是否进行白化操作【使得特征互相独立，且在[0,1]区间内】

3 属性说明

components_

4 举例说明

4.1 导入库&数据集

import numpy as np
from sklearn.decomposition import PCA

X = np.array([[-1,-1,1,1], 
              [-2,-1,5,6], 
              [-3,-2,4,6], 
              [1,1,9,7], 
              [2,1,0,1], 
              [3,2,9,12]])

4.2 生成PCA

pca=PCA(n_components=2).fit(X)

4.3 components_ 

PCA的几个主轴

pca.components_
'''
array([[ 0.16382179,  0.14340848,  0.66107511,  0.7180363 ],
       [ 0.83556307,  0.50546848, -0.13218006, -0.16989525]])
'''

4.4 explained_variance_ &  explained_variance_ratio_

每个主轴方差在总体中的占比。

个人理解为，每个主轴的重要性占比。这个对判断我们n_component_比较有用。

比如我们一开始设置n_component_为3，那么：

pca=PCA(n_components=3).fit(X)

pca.explained_variance_
#array([31.51576789,  6.79717077,  1.44075915]

pca.explained_variance_ratio_
#array([0.79251721, 0.17092634, 0.03623032])

可以看到第三个主轴的方差占比很低，所以我们可以只用两个主轴即可。

pca=PCA(n_components=2).fit(X)

pca.explained_variance_
#array([31.51576789,  6.79717077])

pca.explained_variance_ratio_
#array([0.79251721, 0.17092634])

4.5 singular_values_

每一个主轴对应的特征值

pca.singular_values_
#array([12.55304104,  5.82973874])

4.6 其他attribute

mean_	就是相当于X.mean(axis=0)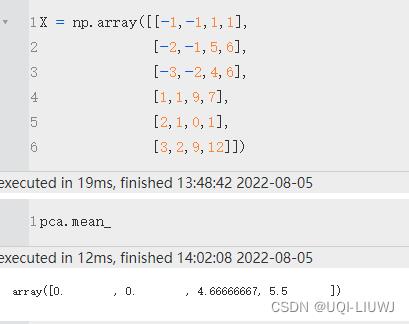
n_components_	主轴个数
n_features_	特征个数

 4.6 函数

fit,fit_transform,transform