数据结构之算法基础

Posted 2022-08-06 爱上口袋的天空

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构之算法基础相关的知识，希望对你有一定的参考价值。

一、简介

什么是算法？
算法的复杂度
算法的分类
一些经典算法

二、为什么要学习算法

1、程序

程序 = 数据结构 + 算法

2、算法——大厂面试的必备主菜

算法可以衡量程序员的技术功底
算法可以体现程序员的学习能力和成长潜力
学习算法有助于提高分析解决问题的能力
学习算法是做性能优化、成长为架构师的必经之路

三、什么是算法(Algorithm)

算法，是指解题方案的准确而完整的描述，是一系列解决问题的清晰指令，算法代表着用系统的方法描述解决问题的策略机制。也就是说，能够对一定规范的输入，在有限时间内获得所要求的输出。

四、算法的特性

有穷性（Finiteness）
算法必须能在执行有限个步骤之后终止；
确切性（Definiteness）
算法的每一步骤必须有确切的定义
输入项（Input）
一个算法有0个或多个输入，以描述运算对象的初始情况
输出项（Output）
一个算法有一个或多个输出，以反映对输入数据加工后的结果
可行性（Effectiveness）
算法中每个计算步骤都可以在有限时间内完成（也称之为有效性）

五、算法的复杂度

如何分析算法的优劣？
求和：1 + 2+ 3 + ... + 100
时间复杂度
执行算法所需要的计算工作量
空间复杂度
算法需要消耗的内存空间

六、算法的时间复杂度

我们考虑的问题
不同的机器，计算速度不同
如果我们的计算机无限快，那只要确定算法能够终止就可以，所有算法性能没有比较的必要了
如果输入数据量很小，那一般机器也都可以在非常短的时间内完成，算法性能也没有必要比较了
计算资源有限，输入数据量很大的情况下，不同算法耗费的时间差异极大
基本指令——程序执行消耗的时间单位
算术指令、数据移动指令、控制指令
int a = 1；运行时间 1
if (a > 1) 运行时间 1
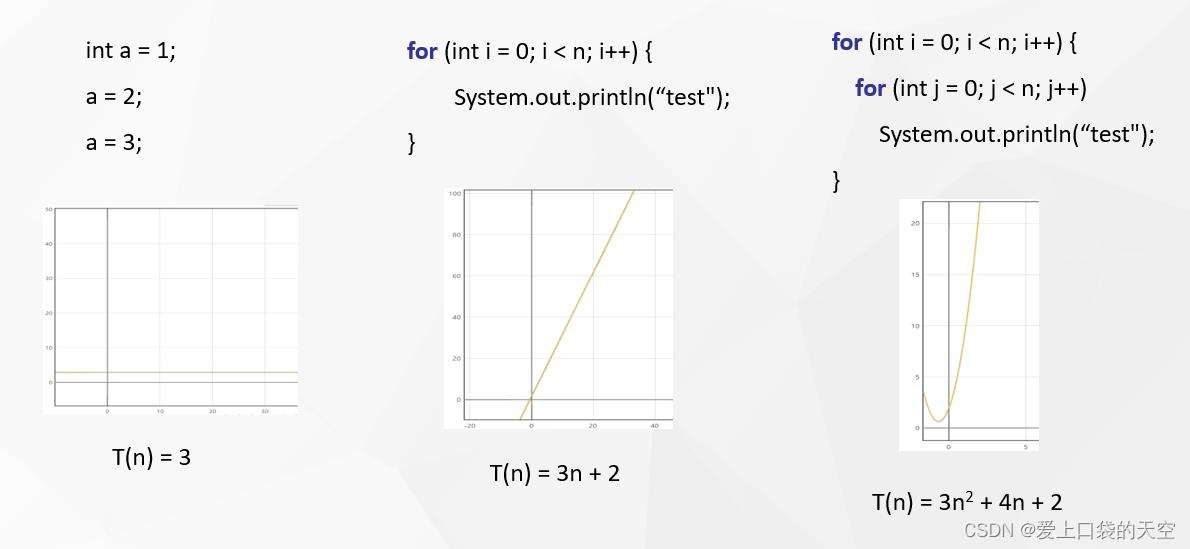
for (int i = 0; i < N; i++) System.out.println(i); 运行时间 3N+2
1、首先i=0,赋予变量i=0,算作1
2、每一次都判断i<n,从0开始，判断到i<n时，经历n+1次，算作N+1
3、i++,从0开始，加到n，算作N，i=0之前已经算过了
4、System.out.println(i)，打印0到N-1,算作N
5、最终的结果1+N+1+N+N = 3N+2

七、时间复杂度

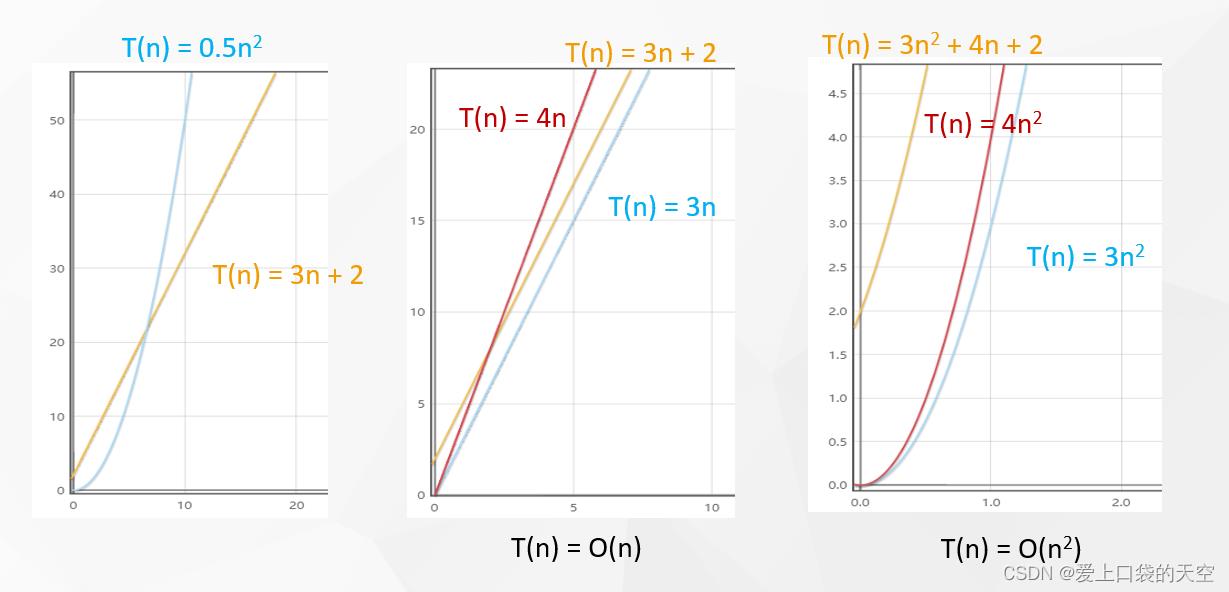
不同的算法，运行时间 T(n) 随着输入规模 n 的增长速度，是不同的

1、复杂度的大O表示法

•对于给定的函数g(n)，用O(g(n))来表示以下函数的集合：

• O(g(n)) = f(n): 存在正常量 c 和 n0，使对所有 n≥n0 ，有 0≤f(n) ≤ cg(n)

•算法分析中，一般用大O符号来表示函数的渐进上界

•这表示，当数据量达到一定程度时，g(n) 的增长速度不会超过 O(g(n)) 限定的范围

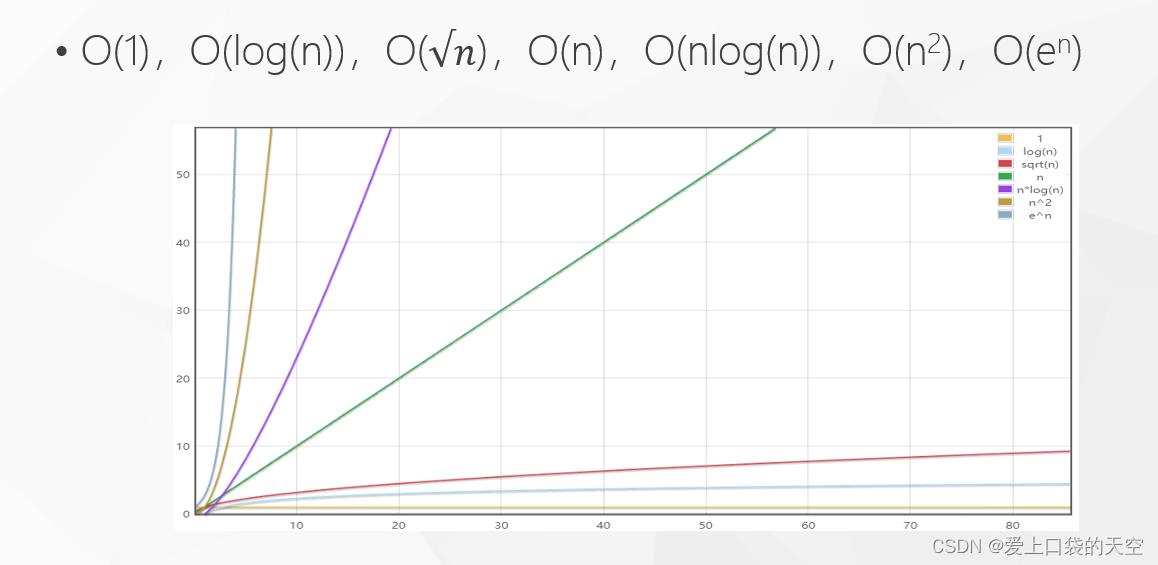
2、常见的算法复杂度

八、空间复杂度

1、算法执行所占用的空间

Array[100] ： O(100)
Array[N] ： O(N)
int val = 1; 空间复杂度 O(1)

有时候递归调用，需要计算调用栈所占用的空间

九、算法的分类

1、按照应用目的

搜索算法
排序算法
字符串算法
图算法
最优化算法
数学算法

2、按照实现策略

暴力法
增量法
分治法
贪心算法
动态规划法
回溯法
分支限界法

十、分治算法

分而治之
问题的规模越小，越容易解决
把复杂问题不断分成多个相同或相似的子问题，直到每个子问题可以简单地进行求解
将所有子问题的解合并起来，就是原问题的解
分治和递归
产生的子问题形式往往和原问题相同，只是原问题的较小规模表达
使用递归手段求解子问题，可以很容易地将子问题的解合并，得到原问题的解
基本步骤
step1：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题
step2：若子问题规模较小而容易被解决则直接解，否则递归地解各个子问题
step3：将各个子问题的解合并为原问题的解
应用场景
二分搜索、大整数乘法、归并排序、快速排序
棋盘覆盖问题、循环赛日程表问题、汉诺塔问题等