数据挖掘之数据预处理
Posted Caaaaaan
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据挖掘之数据预处理相关的知识,希望对你有一定的参考价值。
数据质量
被广泛接受的数据质量的测量标准:
- 准确性
- 完整性(存在缺失值)
- 一致性
- 合时性(数据过时)
- 可信性(数据库来源)
- 解释性
数据预处理
数据预处理的目的是,提高数据质量
主要任务
- 数据清理
- 填写缺失值
- 平滑噪声数据
- 识别或删除离群
- 解决不一致问题
- 数据集成
- 整合多个数据库
- 多维数据集或文件
- 数据缩减
- 降维
- 降数据(Numerosity reduction)
- 数据压缩
- 数据转换和数据离散化
- 规范化
- 离散化
数据清洗
处理缺失值
-
忽略元组(即删除单一对象)
当类标号缺少时通常这么做(监督式机器学习中训练集缺乏类标签)
- 类标号指的是预测类型的训练集中,最后的预测结果缺失
当每个属性(即字段)缺少值比例比较大,效果比较差
- 这种情况下,会使得数据集规模变小太多
- 可以考虑删除单一属性
-
手动填写:工作量大
-
自动填写:使用属性的平均值填充(常用)
df_values=df_values.drop((miss_data[miss_data['total']>200]).index,axis=1)
df_values['pres'].fillna(df_values['pres'].mean(),inplace=True)
df_values['mass'].fillna(df_values['mass'].mean(),inplace=True)
df_values['plas'].fillna(df_values['plas'].mean(),inplace=True)
处理噪音数据
-
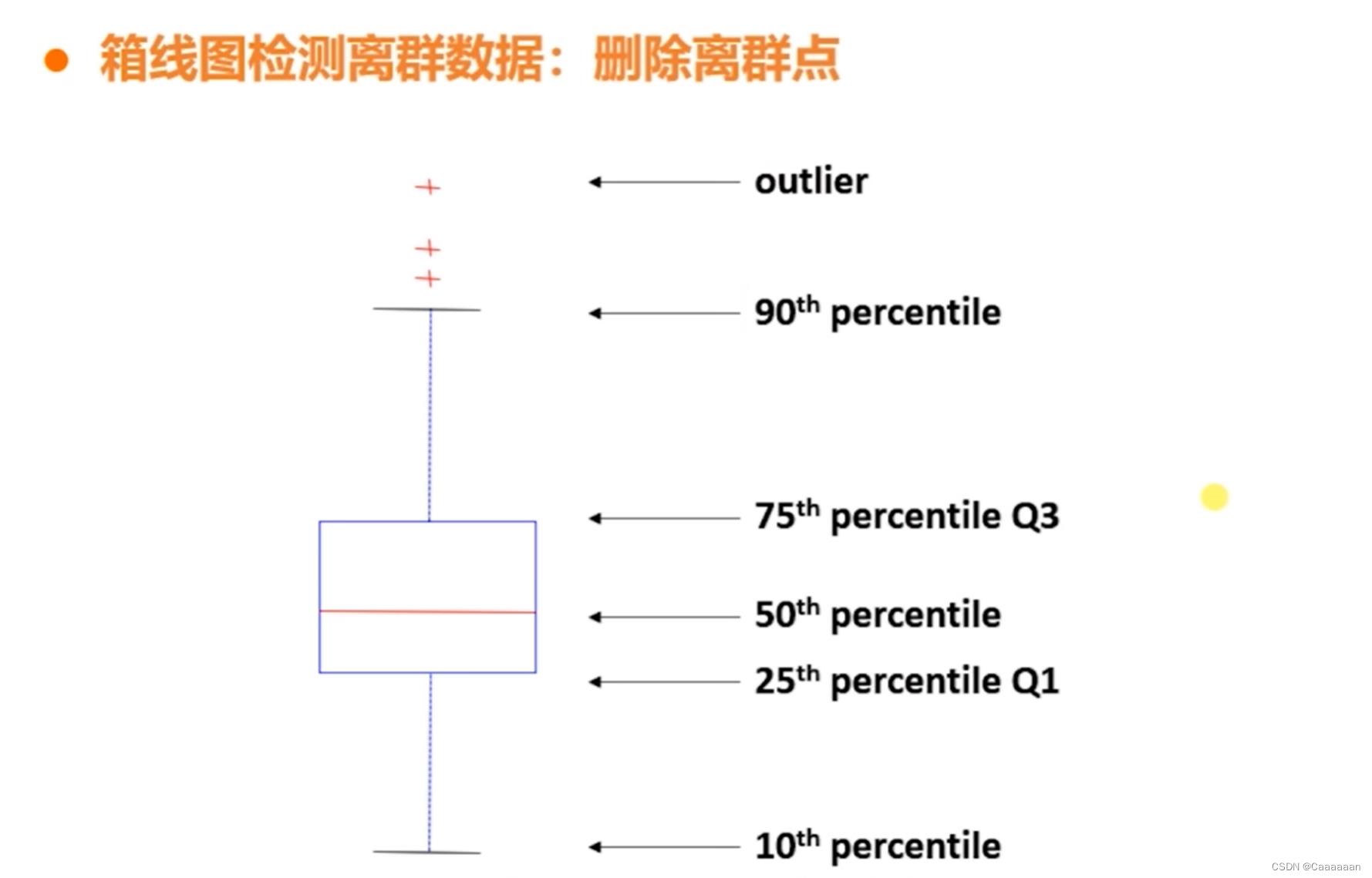
箱型图检测离群数据:删除离群点
当离群点很多时,也会导致数据集规模变小
处理不一致的数据
- 计算推理、替换
- 全局替换
数据集成
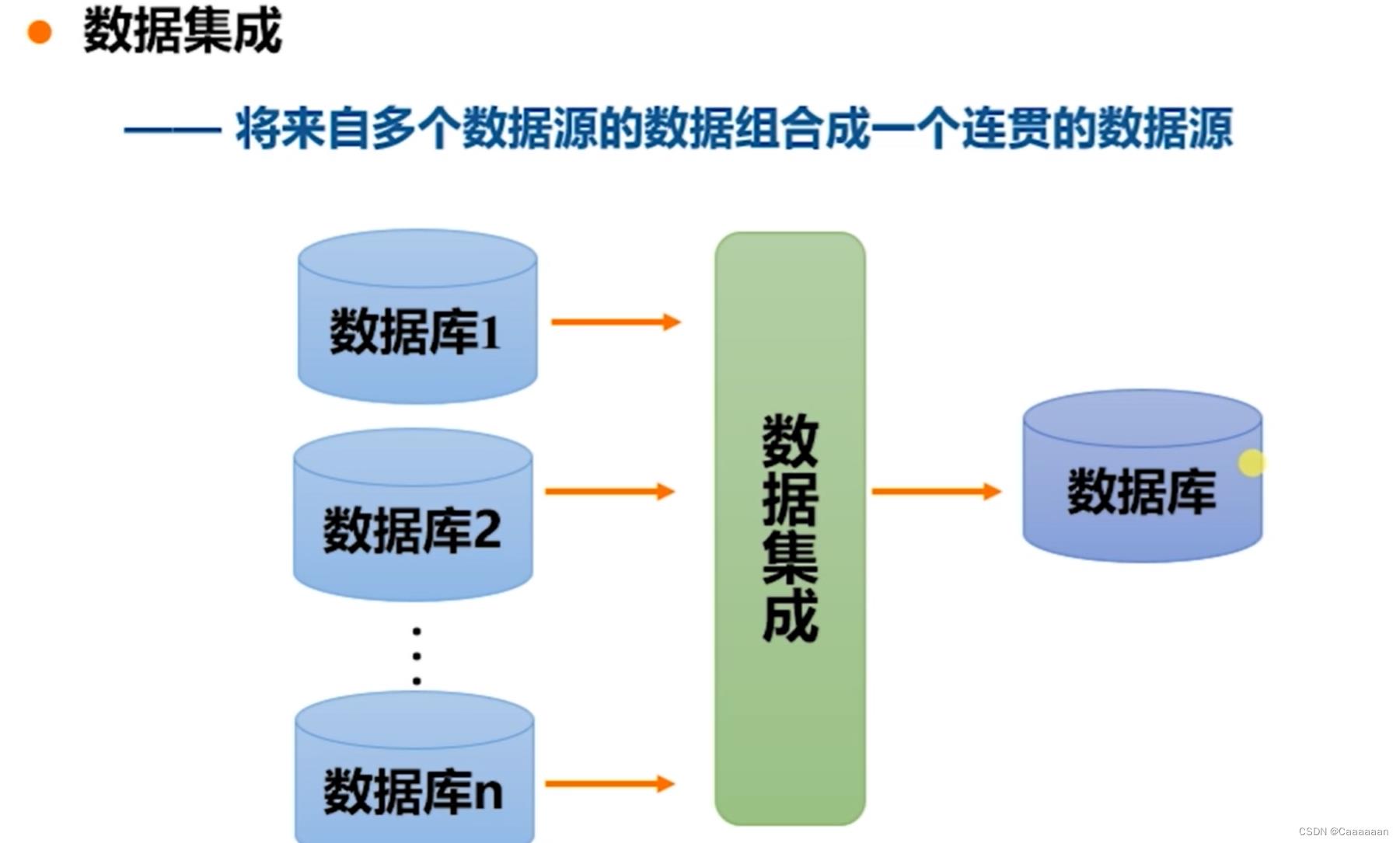
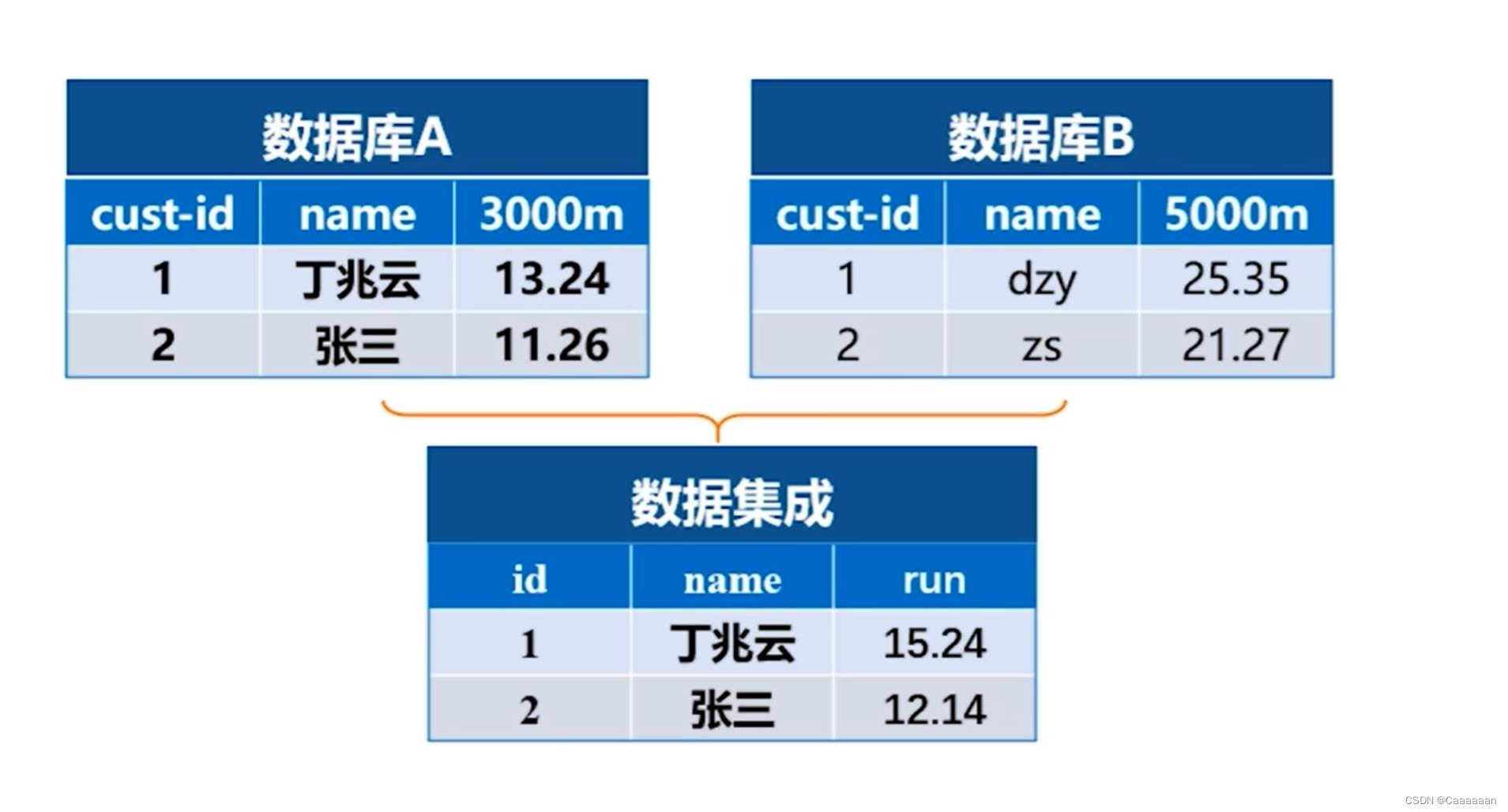
数据集成:将来自多个数据源的数据组合成一个连贯的数据源
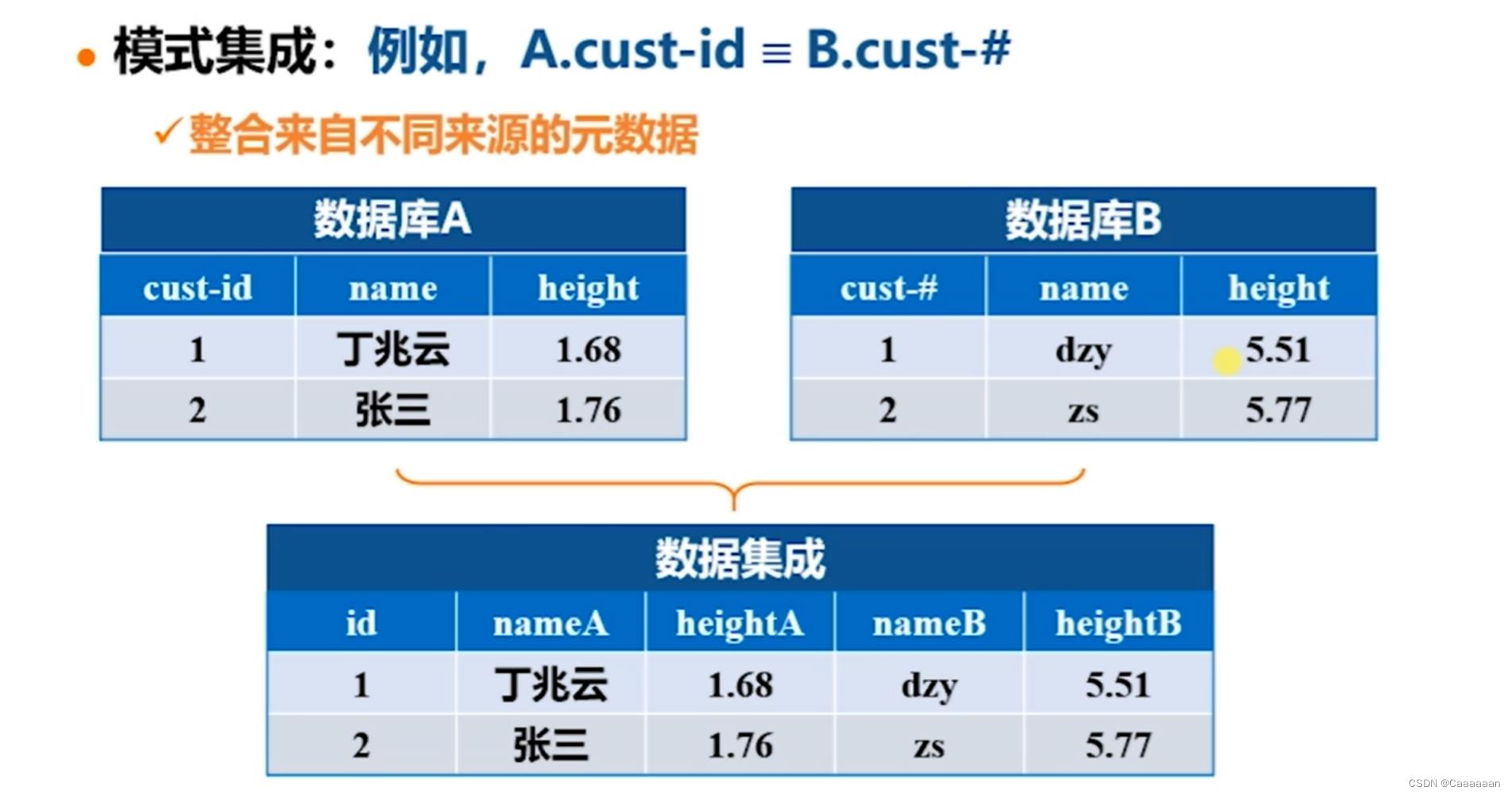
模式集成
- 即当两个数据集的字段名不同,但是表达内容相同时,进行集成处理
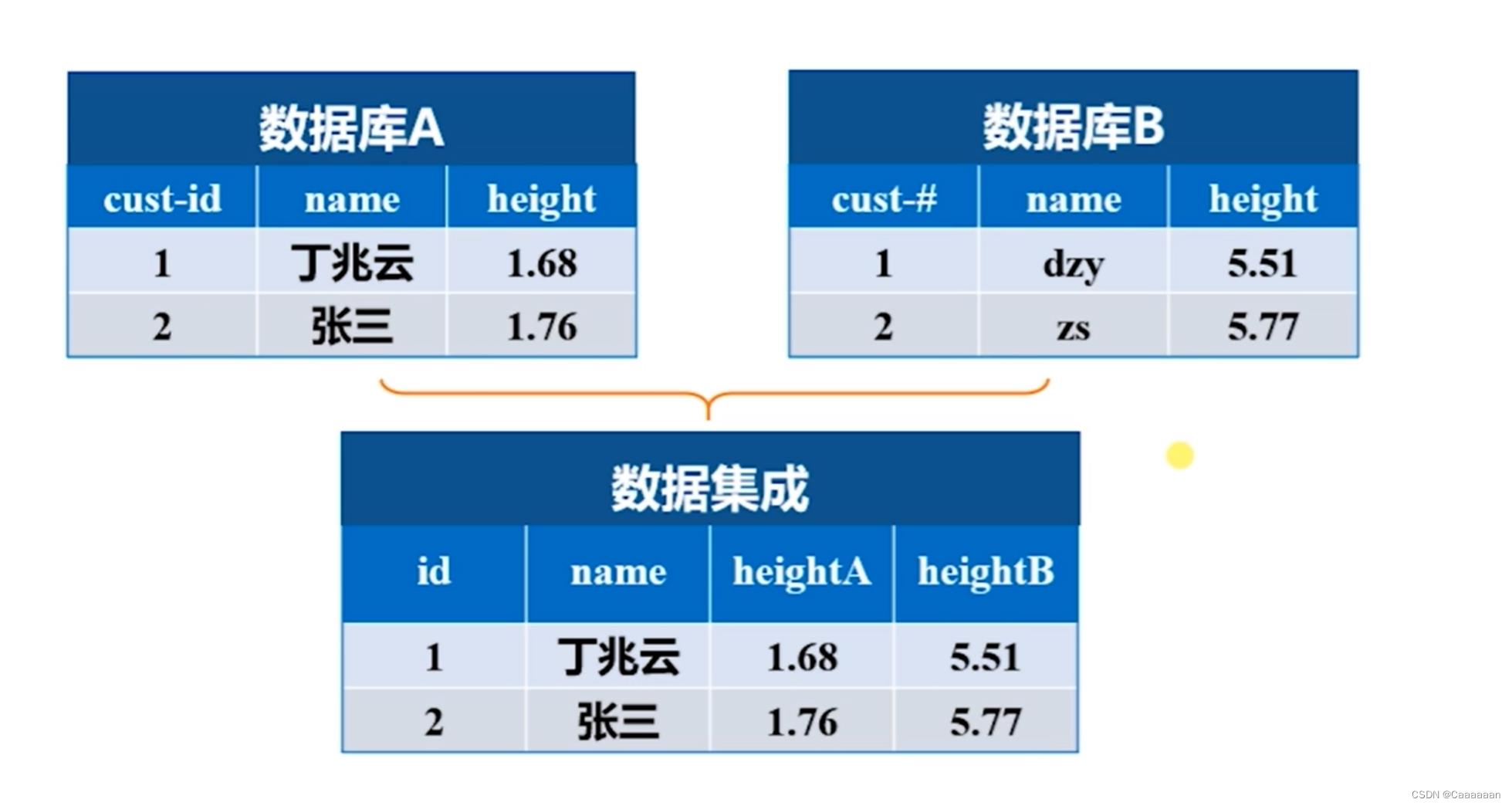
实体识别问题
- 当其中一个数据集,名字用的是中文名,但是另一个数据集用的是英文名
- 但是他们表达的是同一个人(即同一个实体,因此在这种环境下,我们需要对实体识别,再集成)
数据冲突检测和解决
- 对于同一个真实世界的实体,来自不同源的属性值
- 可能的原因:表述方式的不同,尺度的不同(如公制与英制单位)
即如上图,描述高度这个实体,这个数值不一样(单位不一样)
冗余信息的处理
如:一个数据集中有3000m的成绩,另一个有5000m的成绩,则集成为跑步能力进行衡量
- 相同属性或对象可能有不同的文字在不同的数据库中
- 一个属性可能是“派生”的另一个表中的属性,例如跑步能力
- 通过相关性分析和协方差分析可以检测到冗余的属性
- 仔细集成来自多个数据源,可能有助于减少/避免冗余和不一致的地方,并提高读取速度和质量
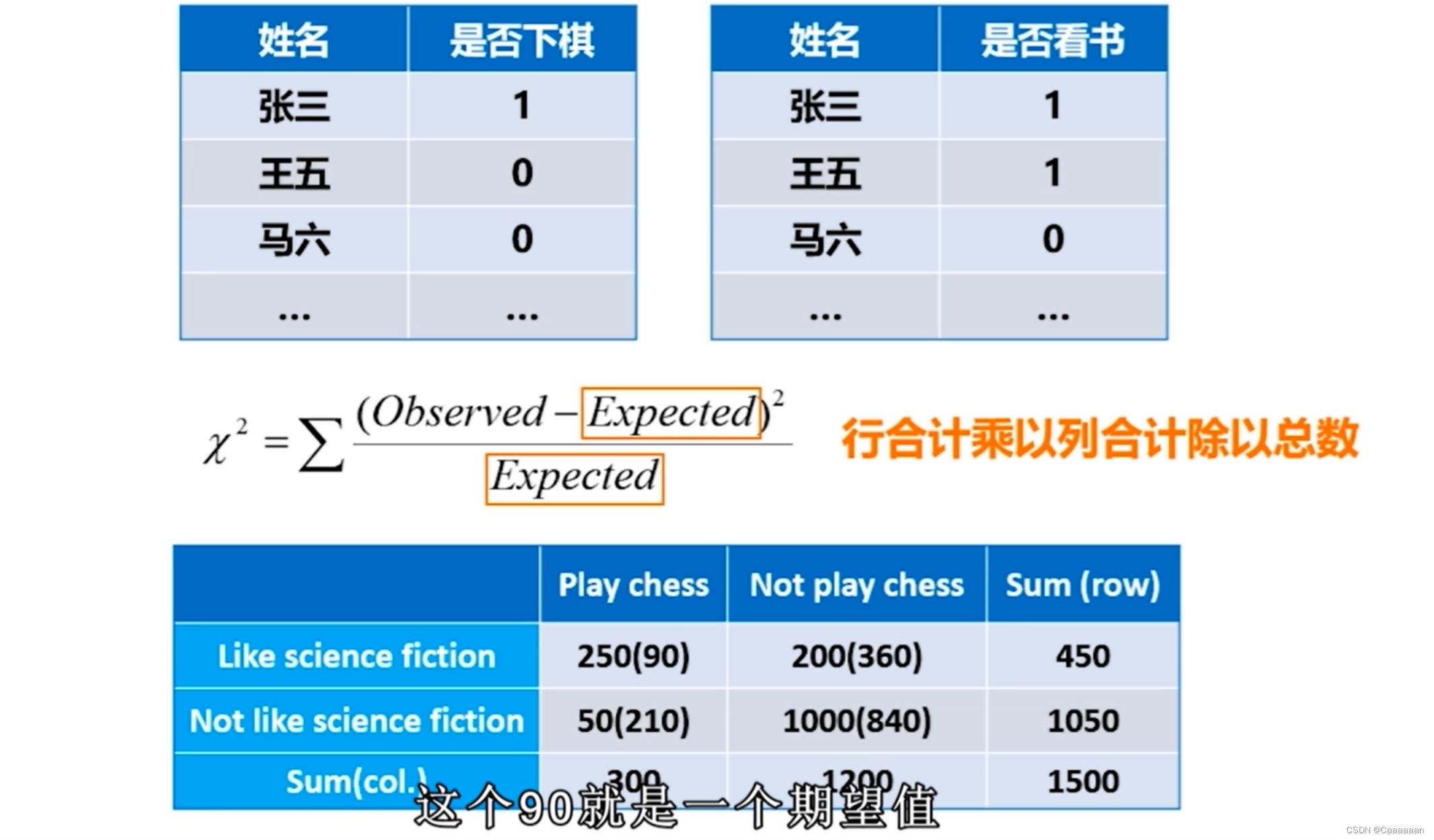
相关分析——离散变量
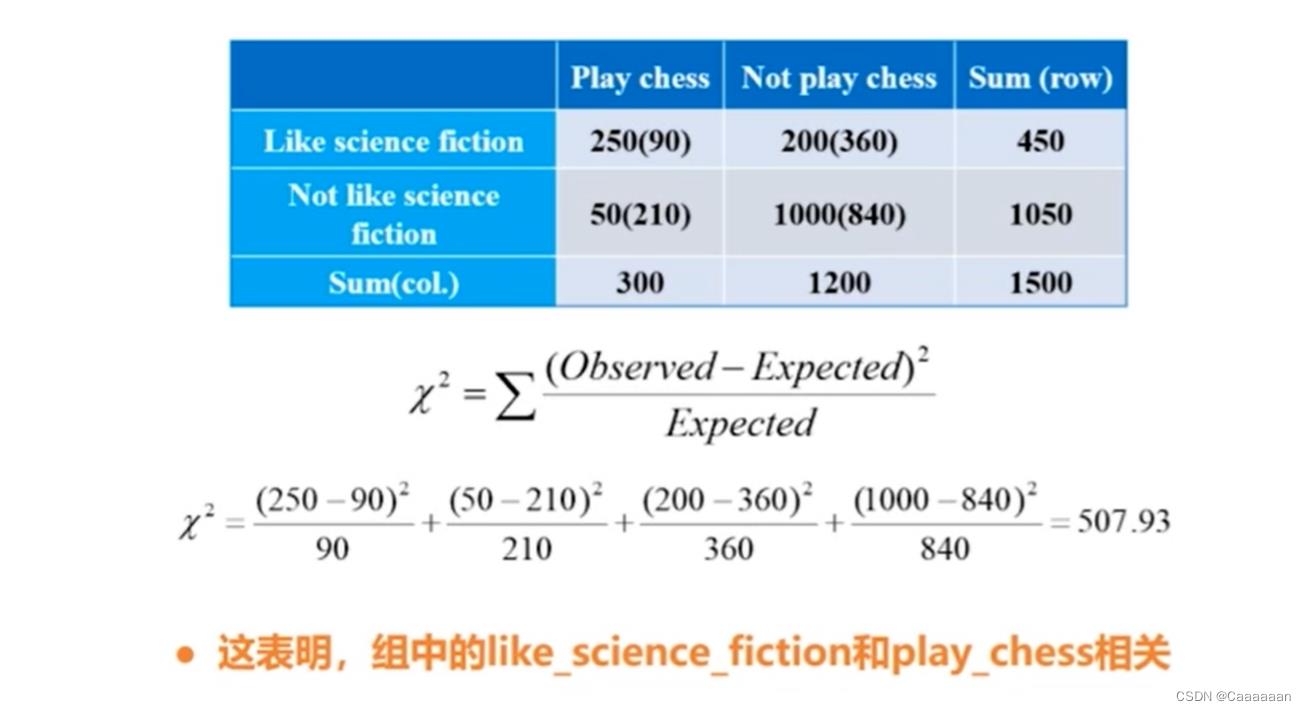
卡方测试 χ 2 ( c h i − s q u a r e ) t e s t χ 2 = ∑ ( O b s e r v e d − E x p e c t e d ) 2 E x p e c t e d ∙ χ 2 值越大,越有可能变量是相关的 ∙ 相关性并不意味着因果关系 卡方测试\\\\ \\chi^2(chi-square)test\\\\ \\chi^2=\\sum\\frac(Observed-Expected)^2Expected\\\\ \\bullet \\chi^2值越大,越有可能变量是相关的\\\\ \\bullet 相关性并不意味着因果关系 卡方测试χ2(chi−square)testχ2=∑Expected(Observed−Expected)2∙χ2值越大,越有可能变量是相关的∙相关性并不意味着因果关系
-
第一个数是统计值,既喜欢下棋,又喜欢科幻小说
-
括号里的值是期望值
-
期望值的计算是通过对应行合计*对应列合计/总数
如450*300/1500=90
-
得到期望值和统计值之后,就可以得到对应的卡方测试
相关分析——连续变量
连续变量没有办法对统计值和期望值进行计数
- 相关系数——皮尔逊相关系数
- 可用corr()得到相关系数矩阵后,使用热力图
皮尔逊相关系数 r p , q = ∑ ( p − p ‾ ) ( q − q ‾ ) ( n − 1 ) σ p σ q = ∑ ( p q ) − n p ‾ q ‾ ( n − 1 ) σ p σ q 皮尔逊相关系数\\\\ r_p,q=\\frac\\sum(p-\\overlinep)(q-\\overlineq)(n-1)\\sigma_p\\sigma_q=\\frac\\sum(pq)-n\\overlinep\\,\\overlineq(n-1)\\sigma_p\\sigma_q 皮尔逊相关系数rp,q=(n−1)σpσq∑(p−p)(q−q)=(n−1)σpσq∑(pq)−npq
-
其中n是元组的数目,而p和q是各自属性的具体值, σ p \\sigma_p σp和 σ q \\sigma_q σq是各自的标准偏差
-
当r>0是,表示两变量正相关;r<0时,两变量负相关
-
当|r|=1时,表示两变量为完全线性相关,即函数关系
-
当r=0时,表示两变量间无线性相关关系
-
当0<|r|<1,表示两变量存在一定程度的线性相关。
- 而且当|r|越接近1,两变量间线性关系越密切;
- |r|越接近于0时,表示两变量的线性相关越弱。
-
一般可按三级划分
- |r|<0.4为低度线性相关
- 0.4<=|r|<0.7为显著性相关
- 0.7<=|r|<1为高度线性相关
协方差
- 协方差也用于表示两组数据的相关性
协方差与相关系数的转化 r p , q = C o v ( p , q ) σ p σ q 协方差与相关系数的转化\\\\ r_p,q=\\fracCov(p,q)\\sigma_p\\sigma_q 协方差与相关系数的转化rp,q=σpσqCov(p,q)
协方差公式 C o v ( p , q ) = E ( ( p − p ‾ ) ( q − q ‾ ) ) = ∑ i = 1 n ( p i − p ‾ ) ( q i − q ‾ ) n 可简化为: C o v ( A , B ) = E ( A ∗ B ) − A ‾ B ‾ 协方差公式\\\\ Cov(p,q)=E((p-\\overlinep)(q-\\overlineq))\\\\ =\\frac\\sum_i=1^n(p_i-\\overlinep)(q_i-\\overlineq)n\\\\ 可简化为:\\\\ Cov(A,B)=E(A*B)-\\overlineA\\,\\overlineB 协方差公式Cov(p,q)=E((p−p)(q−q))=n∑i=1n(pi−p)(qi−q)可简化为:Cov(A,B)=E(A∗B)−AB
-
其中n是元组的数目,而p和q是各自属性的具体值, σ p \\sigma_p σp和 σ q \\sigma_q σq是各自的标准偏差
-
正相关: C o v ( p , q ) > 0 Cov(p,q)>0 Cov(p,q)>0
-
负相关: C o v ( p , q ) < 0 Cov(p,q)<0 Cov(p,q)<0
-
独立性: C o v p ( p , q ) = 0 Covp(p,q)=0 Covp(p,q)=0
-
可具有某些对随机变量的协方差为0,但不是独立的
-
需要一些额外的假设,例如数据是否服从多元正态分布,做了协方差为0意味着独立
注意:
-
独立性 ⇒ C o v ( p , q ) = 0 \\Rightarrow Cov(p,q)=0 ⇒Cov(p,q)=0
-
C o v ( p , q ) = 0 ⇏ Cov(p,q)=0\\nRightarrow Cov(p,q)=0⇏独立性
数据规约
- 由于数据仓库可以存储TB的数据,因此在一个完整的数据集上运行时,复杂的数据分析可能需要一个很长的时间
降维
将高维数据,通过一些方法将高维数据变成低维数据
例如:面对一份成绩的数据集,有6个科目作为属性(语数英物化生),我们可以通过降维将属性变成——文科成绩和理科成绩两个维度
-
原因:
-
随着维数的增加,数据会变得越来越稀疏
- 例如在病例的数据集中,随着维度的增加,会有大量的正常值涌出,使得我们需要关注的生病数据被淹没
-
子空间的可能的组合将成倍增长
- 基于规则的分类方法,建立的规则将组合成倍增长
- 维度越高,可能会导致特征的规则越复杂
-
类似神经网络的机器学习方法,主要需要**学习各个特征的权值参数。**特征越多,需要学习的参数就越多,则模型越复杂
y ^ = s i g n ( ω 1 x 1 + ω 2 x 2 + . . . + ω d x d − t ) \\widehaty=sign(\\omega_1x_1+\\omega_2x_2+...+\\omega_dx_d-t)\\\\ y =sign(ω1x
-