LeetCode 剑指 Offer II 115.重建序列：图解 - 拓扑排序

Posted 2022-08-04 Tisfy

【LetMeFly】图解：剑指 Offer II 115.重建序列 - 拓扑排序

力扣题目链接：https://leetcode.cn/problems/ur2n8P/

请判断原始的序列 org 是否可以从序列集 seqs 中唯一地 重建 。

序列 org 是 1 到 n 整数的排列，其中 1 ≤ n ≤ 10⁴。重建 是指在序列集 seqs 中构建最短的公共超序列，即  seqs 中的任意序列都是该最短序列的子序列。

 

示例 1：

输入: org = [1,2,3], seqs = [[1,2],[1,3]]
输出: false
解释：[1,2,3] 不是可以被重建的唯一的序列，因为 [1,3,2] 也是一个合法的序列。

示例 2：

输入: org = [1,2,3], seqs = [[1,2]]
输出: false
解释：可以重建的序列只有 [1,2]。

示例 3：

输入: org = [1,2,3], seqs = [[1,2],[1,3],[2,3]]
输出: true
解释：序列 [1,2], [1,3] 和 [2,3] 可以被唯一地重建为原始的序列 [1,2,3]。

示例 4：

输入: org = [4,1,5,2,6,3], seqs = [[5,2,6,3],[4,1,5,2]]
输出: true

 

提示：

• 1 <= n <= 104
• org 是数字 1 到 n 的一个排列
• 1 <= segs[i].length <= 105
• seqs[i][j] 是 32 位有符号整数

 

注意：本题与主站 444 题相同：https://leetcode-cn.com/problems/sequence-reconstruction/

方法一：拓扑排序

我们根据样例来分析：

样例一：

nums = [1,2,3], sequences = [[1,2],[1,3]]

样例一中，我们已知排列[1, 2, 3]的两个子序列[1, 2]和[1, 3]。这就说明：1必须出现在2的前面并且1必须出现在3的前面。（因为子序列中元素相对位置必须保持不变）

但是2和3哪个在前哪个在后呢？根据给定输入[[1,2],[1,3]]无法判断。

因此，样例一不能唯一确定“超序列”

样例二：

nums = [1,2,3], sequences = [[1,2],[1,3],[2,3]]

样例二中，我们已知排列[1, 2, 3]的三个子序列[1, 2]、[1, 3]和[2, 3]。这就说明1在2前、1在3前、2在3前。

那么要满足上述三个条件，有且仅有一种排列方式：[1, 2, 3]

因此样例二能唯一确定“超序列”[1, 2, 3]

实现思路：

“1在2前、1在3前”让我们很容易想到拓扑排序。

我们可以构建一张图，图中节点是nums中的每一个元素。如果1在2前就添加一条1→2的边。

那么样例一的图将被构建为：

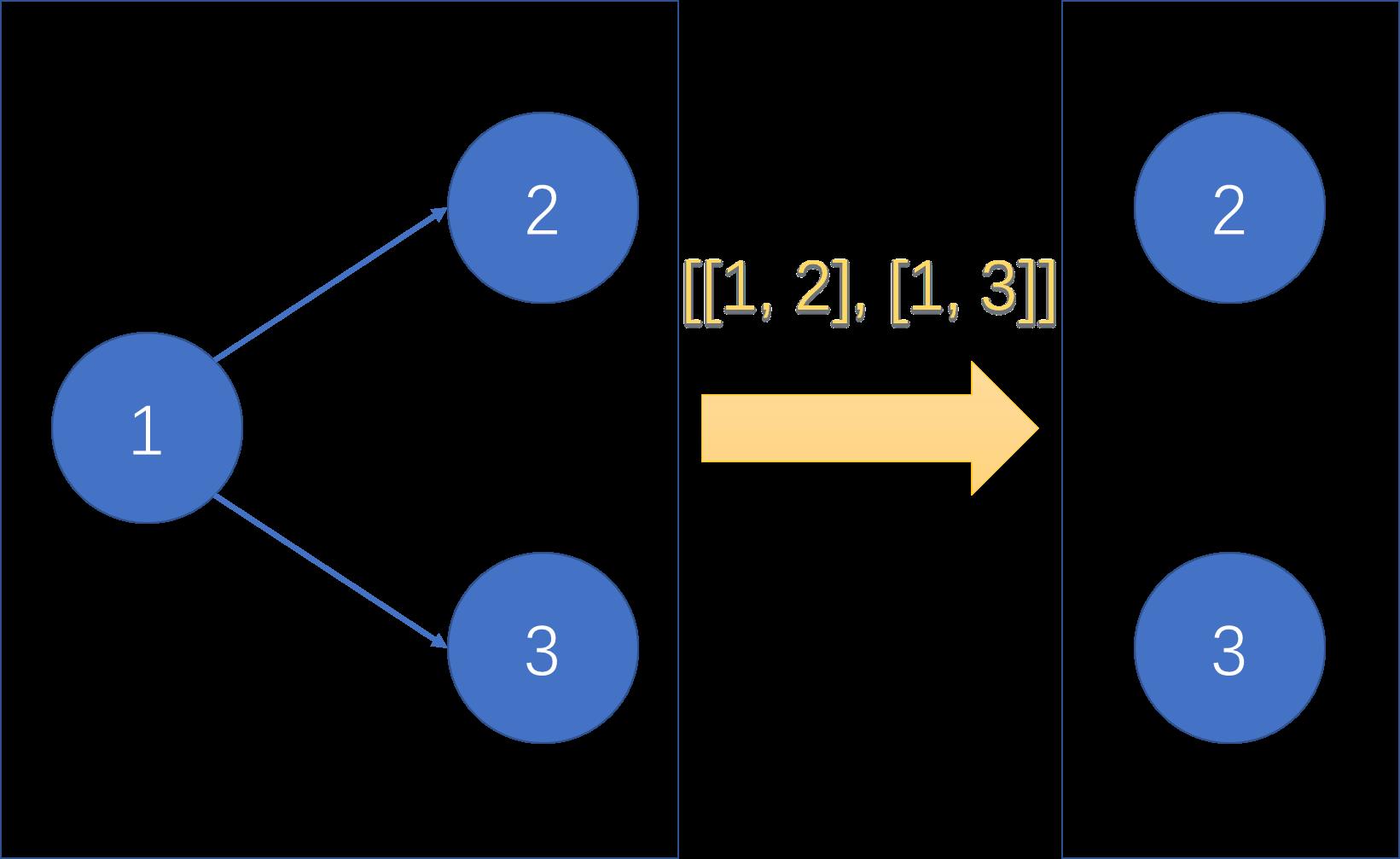
从入度为0的节点1开始进行拓扑排序，排序之后发现剩下两个节点，彼此之间无法确定相对顺序。

样例二的图将被构建为：

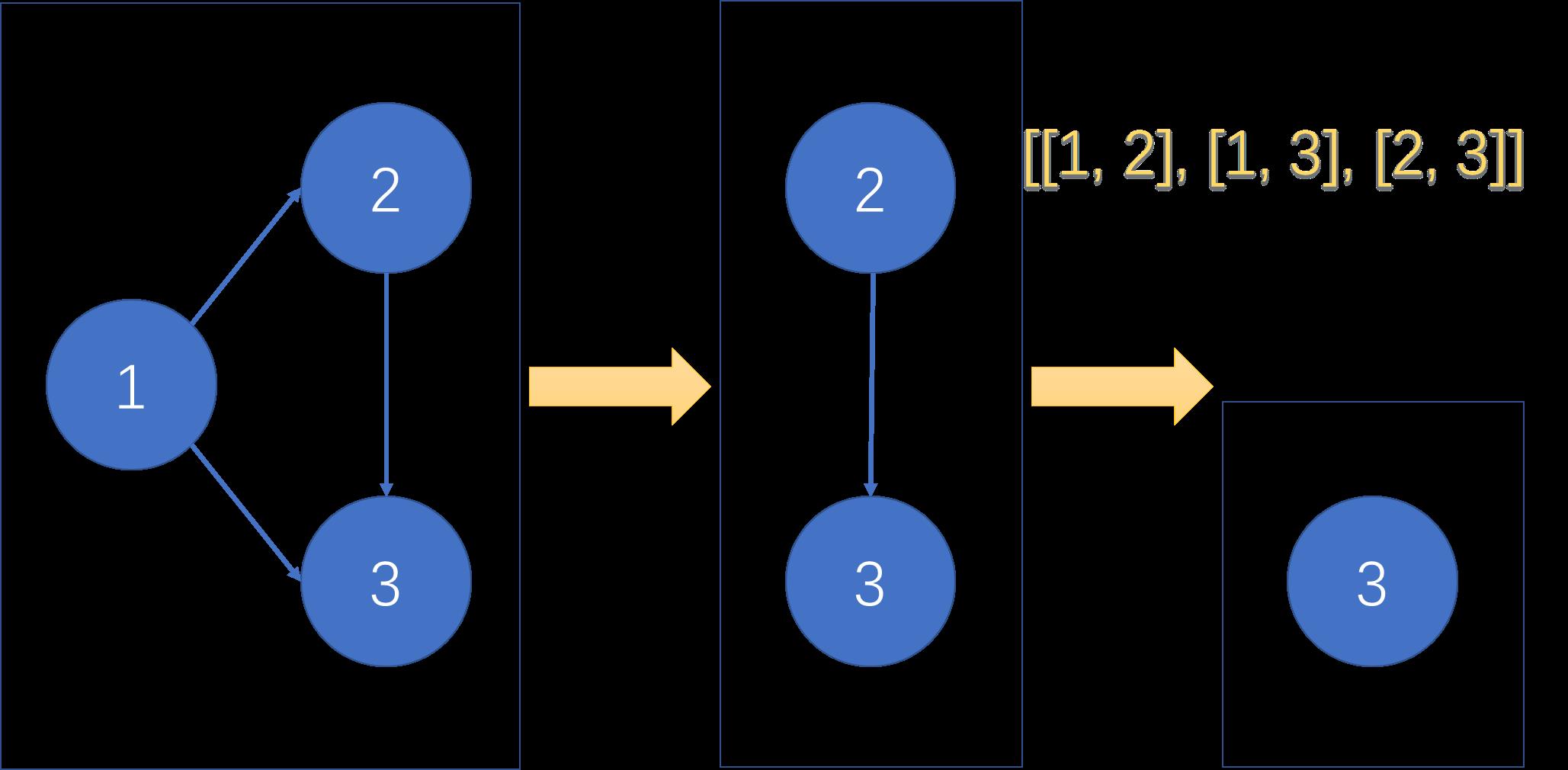
从入度为0的节点1开始进行拓扑排序，排序之后只剩下了最终节点3

具体实现方法

1. 初始时遍历mermaid sequenceDiagrams中的所有元素，对于mermaid sequenceDiagrams中的[a, b, c]，构建一条a→b的边和一条b→c的边，并把b和c的入度+1
2. 遍历所有节点，将入度为0的节点入队。不断从队列中取出节点，去掉从这个节点开始的所有的边，并把去掉的边所指向的节点的入度-1。（假如从节点a出发有两条边a→b和a→c，那么b和c的入度-1）
3. 直到队列为空

注意：

1. 整个排序过程中，队列中最多有1个节点。（那是因为如果同时有多个入度为0的节点，就无法判断这些节点之间的相对顺序）
2. 排序结束后，所有节点的入度必须全部为0

如果同时满足上述两个条件，就返回true

• 时间复杂度$O(n+m)$，其中$n$是排列的长度，$m$是$sequences$中元素的个数
• 空间复杂度$O(n+m)$

AC代码

C++

class Solution 
public:
    bool sequenceReconstruction(vector<int>& nums, vector<vector<int>>& sequences) 
        int n = nums.size();
        vector<vector<int>> from(n + 1);
        vector<int> inDegree(n + 1, 0);
        for (vector<int>& v : sequences) 
            for (int i = 1; i < v.size(); i++)   // v[i - 1] → v[i]
                from[v[i - 1]].push_back(v[i]);
                inDegree[v[i]]++;
            
        
        queue<int> zero;
        for (int i = 1; i <= n; i++) 
            if (inDegree[i] == 0) 
                zero.push(i);
            
        
        while (zero.size()) 
            if (zero.size() != 1)
                return false;
            int thisFrom = zero.front();
            zero.pop();
            for (int& thisTo : from[thisFrom]) 
                inDegree[thisTo]--;
                if (!inDegree[thisTo]) 
                    zero.push(thisTo);
                
            
        
        for (int i = 1; i <= n; i++) 
            if (inDegree[i])
                return false;
        
        return true;
    
;

图片制作不易，喜欢了就点个赞再走吧~

同步发文于CSDN，原创不易，转载请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/125945290