数据结构--链表

Posted 2022-08-04 大扑棱蛾子

这将会使一篇非常长的文章，请做好战斗准备

链表的特点是可以用任意存储单元存储数据元素，它不要求存储单元连续。链表一般分为以下4种：

• 单向链表
• 双向链表
• 单向循环链表
• 双向循环链表

下面我们对这几种链表一一介绍。

ADT

我们先来定义线性表的抽象数据类型。

/**
 * 线性表
 *
 * @author jaune
 * @since 1.0.0
 */
public interface List<E> 

    /**
     * 获取列表的长度
     * @return 列表的长度
     */
    int size();

    /**
     * 判断是否为空
     * @return true - 空； false - 非空
     */
    boolean isEmpty();

    /**
     * 添加元素
     */
    void add(E item);

    /**
     * 将元素插入到指定位置，插入位置所在的元素及其后面的元素后移。
     * @param index 元素位置，从0开始。0 ≤ index < length
     * @param item 数据元素
     * @throws IndexOutOfBoundsException 超出列表长度
     */
    void add(int index, E item);

    /**
     * 替换指定位置的元素
     * @param index 元素位置，从0开始。0 ≤ index < length
     * @param item 数据元素
     * @throws IndexOutOfBoundsException 超出列表长度
     */
    void set(int index, E item);

    /**
     * 删除指定位置的元素，后面的元素前移。
     * @param index 元素位置
     * @return 删除的元素
     */
    E remove(int index);

    /**
     * 获取指定位置的元素，如果超出列表长度，抛出异常
     * @param index 元素位置
     * @throws IndexOutOfBoundsException 超出列表长度
     */
    E get(int index);

    /**
     * 清空列表
     */
    void clear();

由于Java是面向对象的，所以与C语言相比，ADT会有很大的差异。

单向链表

单向链表的数据元素包含两个域，一个是存储数据元素信息的数据域，一个是存储后继存储位置的指针域。这两部分组成的数据元素$a_i$的存储映像，称为结点。指针域中存储的信息称做指针或链。由于每个结点只包含一个指针域，故又称线性链表或单链表。

在单向链表中，除头元素外，每个元素的存储位置都包含在其直接前驱结点的信息中。

在单向链表中插入和删除一个元素如下图所示，红色的线表示要删除的关系。

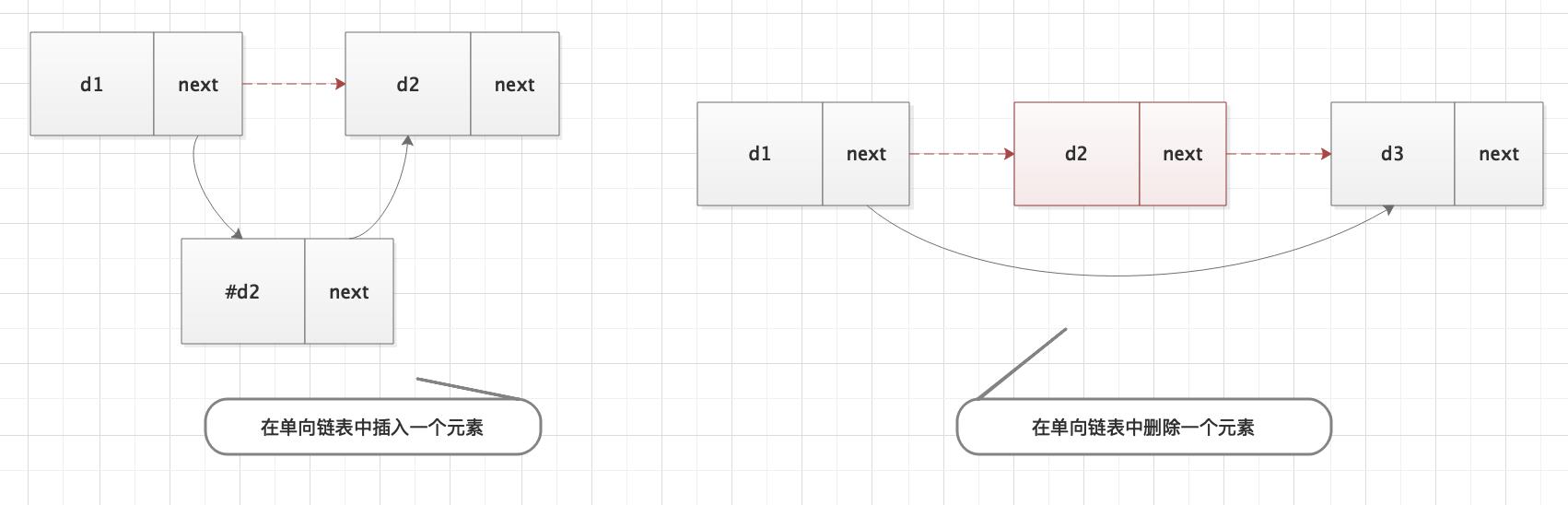
下面我们来实现单向链表，并分析其中这些方法的时间复杂度。

单向线性表的实现

/**
 * 单向链表
 *
 * @author jaune
 * @since 1.0.0
 */
public class SingleLinkedList<E> implements List<E> 

    private Node<E> first;
    private Node<E> last;
    private int size;

    @Override
    public int size() 
        return this.size;
    

    @Override
    public boolean isEmpty() 
        return size == 0;
    

    @Override
    public void add(E item) 
        if (this.first == null) 
            this.first = new Node<>(item);
            this.last = this.first;
         else 
            Node<E> node = new Node<>(item);
            this.last.next = node;
            this.last = node;
        
        this.size ++;
    

    @Override
    public void add(int index, E item) 
        if (index == 0) 
            this.addFirst(item);
         else 
            // 或者前驱数据节点
            Node<E> preNode = this.getNode(index - 1);
            Node<E> node = new Node<>(item);
            node.next = preNode.next;
            preNode.next = node;
        
        this.size++;
    

    @Override
    public void set(int index, E item) 
        if (index == 0) 
            Node<E> node = new Node<>(item);
            node.next = this.first.next;
            // 注意清除引用关系
            this.first.next = null;
            this.first = node;
         else 
            Node<E> preNode = this.getNode(index - 1);
            Node<E> node = new Node<>(item);
            node.next = preNode.next.next;
            preNode.next.next = null;
            preNode.next = node;
        
    

    @Override
    public E remove(int index) 
        Node<E> removeNode;
        if (index == 0) 
            removeNode = this.first;
            Node<E> newFirst = this.first.next;
            removeNode.next = null;
            this.first = newFirst;
         else 
            Node<E> preNode = this.getNode(index - 1);
            removeNode = preNode.next;
            preNode.next = removeNode.next;
            removeNode.next = null;
        
        this.size--;
        return removeNode.item;
    

    @Override
    public E get(int index) 
        return this.getNode(index).item;
    

    @Override
    public void clear() 
        Node<E> item = this.first;
        while (item != null) 
            Node<E> next = item.next;
            item.next = null;
            item = next;
        
        this.first = null;
        this.last = null;
        this.size = 0;
    

    private void addFirst(E item) 
        Node<E> node = new Node<>(item);
        node.next = this.first;
        this.first = node;
    

    private Node<E> getNode(int index) 
        if (index >= 0 && index < this.size) 
            int p = 0;
            Node<E> item = this.first;
            while (item != null) 
                if (p == index) 
                    return item;
                 else 
                    item = item.next;
                    p++;
                
            
            throw new IndexOutOfBoundsException(this.outOfBoundsMsg(index));
         else 
            throw new IndexOutOfBoundsException(this.outOfBoundsMsg(index));
        
    

    private String outOfBoundsMsg(int index) 
        return "Index: "+index+", Size: "+size;
    

    private static class Node<T> 
        T item;
        Node<T> next;

        public Node(T item) 
            this.item = item;
        
    

时间复杂度分析

这里我们只考虑最坏的情况

• size(): $O(1)$
• isEmpty(): $O(1)$
• add(E item): $O(1)$
• add(int index, E item): $O(n)$
• set(int index, E item): $O(n)$
• remove(int index): $O(n)$
• get(int index): $O(n)$

在采用数组实现的线性表中get(int index)方法的时间复杂度为$O(1)$。java中的java.util.ArrayList就是采用数组实现的线性表。set(int index, E item)也是$O(1)$。

add(int index, E item)和remove(int index)会涉及到数组中元素的整体后移或前移，所以在最坏情况下也是$O(n)$。add(E item)会遇到数组扩容的问题，所以最快情况下是$O(n)$。

双向链表

在双向链表的结点中有两个指针域，其一指向直接后继，另一指向直接前驱。

在双向链表中插入和删除时与单向表有着较大的区别，在双向链表中需要同时修改两个方向上的指针。如下图所示。

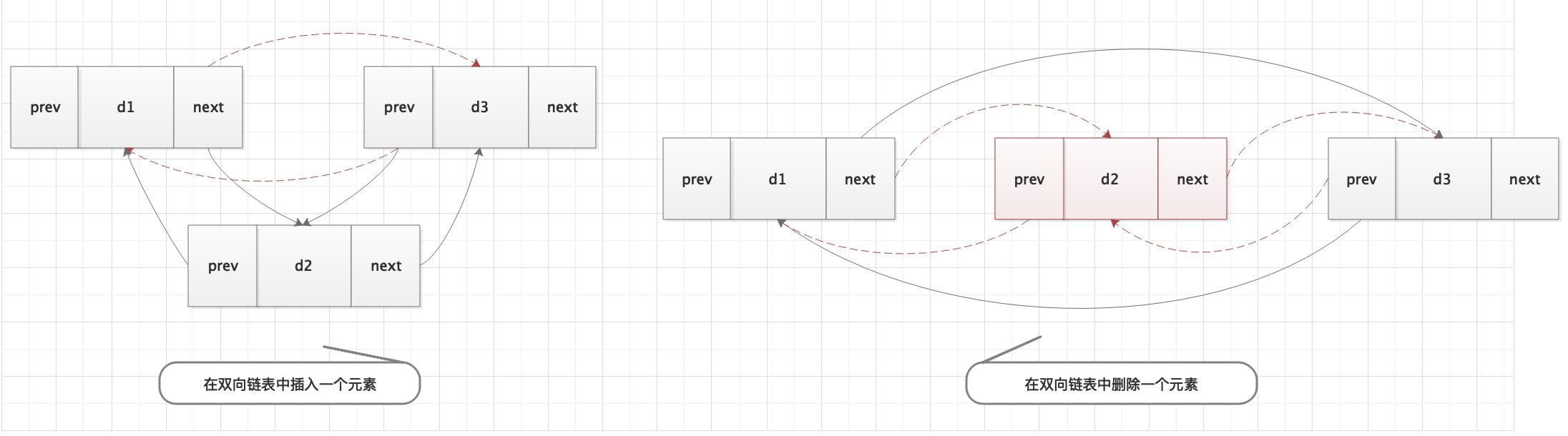
双向链表数据结点的定义如下

private static class Node<T> 
    T item;
    Node<T> next;
    Node<T> prev;

    public Node(T item) 
        this.item = item;
    
    public Node(T item, Node<T> next, Node<T> prev) 
        this.item = item;
        this.next = next;
        this.prev = prev;
    

Java中的java.util.LinkedList就是使用双向链表实现的。具体代码限于篇幅原因，这里就不再实现。只介绍两者中的差异。

双向链表与单向链表最大的差异之一就是节点可以从两个方向进行遍历，即可以从前往后也可以从后忘前。请看下面的代码：

Node<E> node(int index) 
    // assert isElementIndex(index);

    if (index < (size >> 1)) 
        Node<E> x = first;
        for (int i = 0; i < index; i++)
            x = x.next;
        return x;
     else 
        Node<E> x = last;
        for (int i = size - 1; i > index; i--)
            x = x.prev;
        return x;
    

这是JDK中的java.util.LinkedList这段代码的意思就是当要查找的数据元素的索引小于于链表总长度的一半时，就从前往后遍历，否则从后往前遍历。

size >> 1等价于size/2。如00001101 >> 1 = 00000110即13 >> 1 = 6。这里之所以不用除法是因为位运算的计算速度更快。

JDK中有很多优秀的算法和编程思想，读JDK的源码也能对自己的编程能力有很大的提升

除了节点的查找外，另外一个区别就是双向链表可以实现自我删除。我们在删除单向链表的节点时需要找到上一个节点。而在双向链表中我们只需要找到要删除的节点即可。当然还要考虑要删除的节点时头结点或尾节点的问题。

    // jdk中删除节点
    E unlink(Node<E> x) 
        // assert x != null;
        final E element = x.item;
        final Node<E> next = x.next;
        final Node<E> prev = x.prev;

        // 头节点处理
        if (prev == null) 
            first = next;
         else 
            prev.next = next;
            x.prev = null;
        
        // 尾节点处理
        if (next == null) 
            last = prev;
         else 
            next.prev = prev;
            x.next = null;
        

        x.item = null;
        size--;
        modCount++;
        return element;
    

其他代码与单链表类似。读者可以尝试自己实现。

单向循环链表

单向循环链表的特点是最后一个结点的后继结点指向头结点，整体形成一个环。因此从表中任意一结点出发均可找到表中的其他结点。

如果只有一个节点，则其后继指向自己。

单向链表的遍历需要尤其的注意，因为不能再通过判断最后一个结点的后继结点为null来确定已达到链表的尾部。一种方法是记录链表的长度，然后遍历的时候遍历到链表的长度后停止。另一种方法是判断后继结点是否为头结点，如果是头结点说明已达到链表尾部。

双向循环链表

双向循环链表的特点与单向循环链表类似，只是双向循环链表可以从两个方向遍历结点。双向循环链表的尾结点的后继指向头结点，头结点的前驱指向尾结点。

如果只有一个数据元素，则其前驱和后继都指向自己。

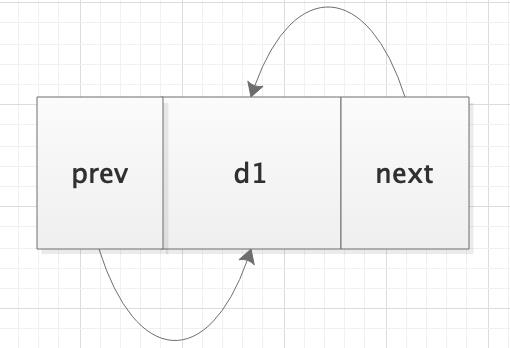
循环链表的代码在此不再实现，有兴趣的读者可以自行实现。