算法模板-深度优先遍历

Posted 2022-08-02 周先森爱吃素

简介

深度优先遍历，顾名思义对于树或者图中的某个节点，尽可能往一个方向深入搜索下去。具体而言，从某个节点v出发开始进行搜索，不断搜索直到该节点的所有边都被遍历完。对于很多树、图和矩阵地搜索问题，深度优先遍历是一个非常有效的解法。

深度优先遍历（DFS）是图论的经典算法，以树为例，DFS尽可能深的搜索每个树枝，一直搜索到最深的那一个为止。对节点v来说，先是访问其子节点v_1_1，然后访问子节点的子节点v_1_1_1，直到到达叶子节点v_1_1_1_1再返回叶子节点的上一层对其他节点继续同样的搜索。下图为DFS的搜索顺序示例图（采用graph_editor绘制）。

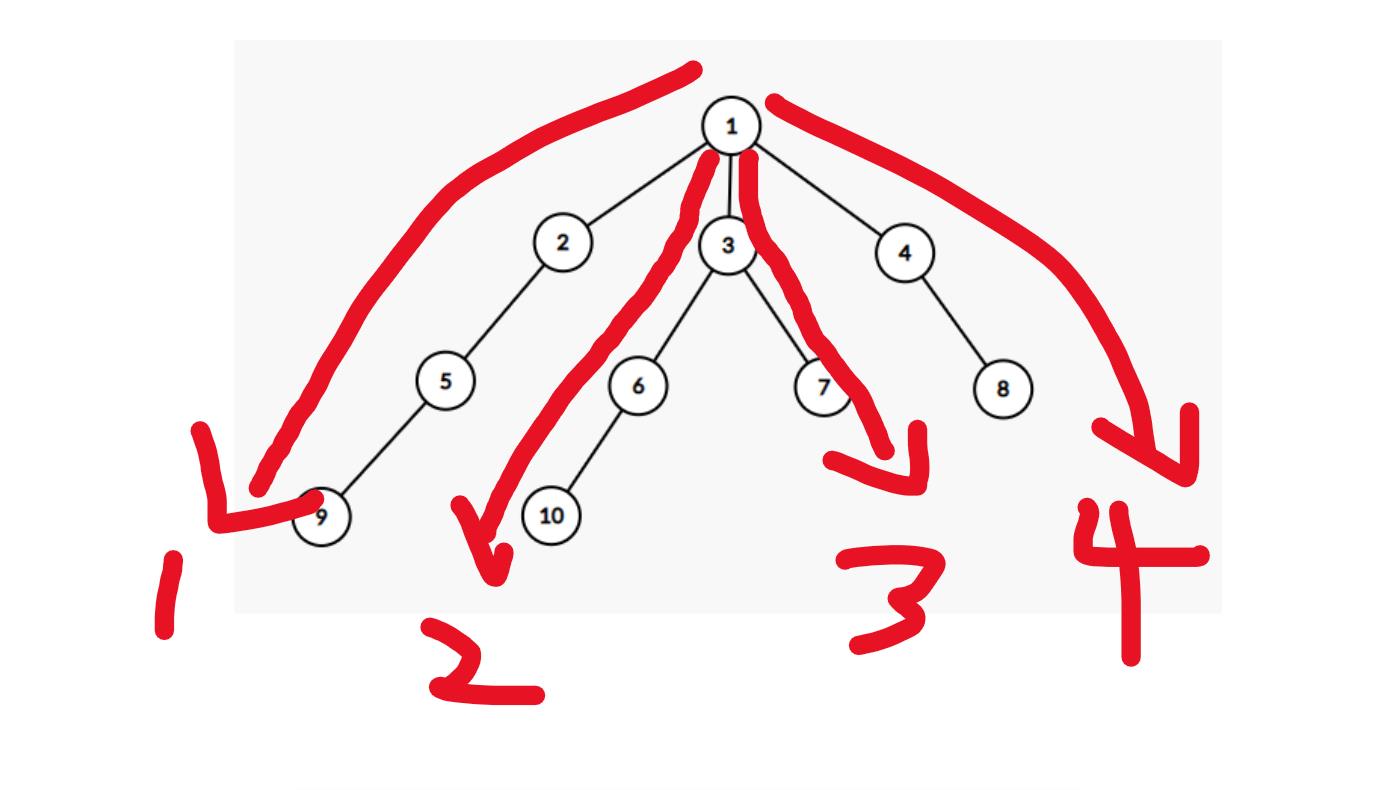
栈实现

显然，从DFS的原理来看，节点的添加顺序若以栈来维护（后进后出）节点的访问，那么可以写出如下的模板。

def dfs(node):
    visited, stack = set(), [node]

    while stack:
        node = stack.pop()
        visited.add(node)
        print(node.val)
        nodes = node.nexts
        stack.append(nodes)

递归实现

当然，我们更多的是使用递归的方法来实现深度优先遍历，其模板代码如下。

def dfs(node):
    if node is None:
        return
    print(node.val)
    for node in node.nexts:
        dfs(node)

练习题

由于使用到DFS的题实在过多，这里也只列举几个典型的作为示例。

79. 单词搜索

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例1：

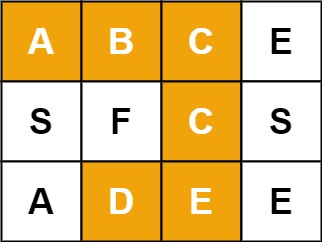
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

这题是典型的存在性检验，我们只需要尽可能远地搜索出一条合适的路径即可，可以采用深度优先遍历算法。

class Solution:
    def exist(self, board: List[List[str]], word: str) -> bool:
        def dfs(i, j, k):
            if not 0 <= i < len(board) or not 0 <= j < len(board[0]) or board[i][j] != word[k]:
                return False
            if k == len(word) - 1:
                return True
            board[i][j] = ""
            rst = dfs(i, j+1, k+1) or dfs(i, j-1, k+1) or dfs(i-1, j, k+1) or dfs(i+1, j, k+1)
            board[i][j] = word[k]
            return rst
        
        for i in range(len(board)):
            for j in range(len(board[0])):
                if dfs(i, j, 0):
                    return True
        return False

补充说明

面对“存在性检验”的搜索题，应当优先考虑基于递归的深度优先遍历呵基于队列的广度优先遍历。