Codeforces Round #377 (Div. 2)题解报告

Posted 2022-07-31 queuelovestack

此文章可以使用目录功能哟↑(点击上方[+])

在大连呆了几天,感觉CF错过好多场,今天补一下昨晚这场...

链接→Codeforces Round #377 (Div. 2)

 Problem A-Buy a Shovel

Accept: 0    Submit: 0
Time Limit: 1 second    Memory Limit : 256 megabytes

 Problem Description

Polycarp urgently needs a shovel! He comes to the shop and chooses an appropriate one. The shovel that Policarp chooses is sold for k burles. Assume that there is an unlimited number of such shovels in the shop.

In his pocket Polycarp has an unlimited number of "10-burle coins" and exactly one coin of r burles (1 ≤ r ≤ 9).

What is the minimum number of shovels Polycarp has to buy so that he can pay for the purchase without any change? It is obvious that he can pay for 10 shovels without any change (by paying the requied amount of 10-burle coins and not using the coin of r burles). But perhaps he can buy fewer shovels and pay without any change. Note that Polycarp should buy at least one shovel.

 Input

The single line of input contains two integers k and r (1 ≤ k ≤ 1000, 1 ≤ r ≤ 9) — the price of one shovel and the denomination of the coin in Polycarp's pocket that is different from "10-burle coins".

Remember that he has an unlimited number of coins in the denomination of 10, that is, Polycarp has enough money to buy any number of shovels.

 Output

Print the required minimum number of shovels Polycarp has to buy so that he can pay for them without any change.

 Sample Input

117 3
237 7
15 2

 Sample Output

9
1
2

 Hint

In the first example Polycarp can buy 9 shovels and pay 9·117 = 1053 burles. Indeed, he can pay this sum by using 10-burle coins and one 3-burle coin. He can't buy fewer shovels without any change.

In the second example it is enough for Polycarp to buy one shovel.

In the third example Polycarp should buy two shovels and pay 2·15 = 30 burles. It is obvious that he can pay this sum without any change.

 Problem Idea

解题思路:

【题意】

题目blablabla讲了一大段,概括一下其实就那么几句

给你k和r

求最小的i,使得i*k%10==0或i*k%10==r

【类型】
暴力
【分析】

Polycarp有无限个面值为10的硬币和一个面值为r(1≤r≤9)的硬币,要买铲子(商店铲子也有无限个)

问最小需要买多少个铲子,才能够让售货员不用找零

不用找零有两种情况:

①只用面值为10的硬币购买

这种情况,所买的铲子价格之和必定得是10的倍数,才不用找零

即i*k%10==0

②除用了面值为10的硬币之外,面值为r的硬币也用了

由于面值为10的硬币加起来必定能被10整除,所以多一个面值为r的硬币,对10取模则余r

即i*k%10==r

由于i=10时,i*k必定能被10整除,故此题可以采取暴力做法

毕竟暴力最多不会超过10次取模运算

【时间复杂度&&优化】
O(1)

题目链接→Codeforces Problem 732A Buy a Shovel

 Source Code

/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 100005;
const int M = 100005;
const int inf = 1000000007;
const int mod = 1000000007;
int main()

    int k,r,i;
    scanf("%d%d",&k,&r);
    for(i=1;;i++)
        if(i*k%10==0||i*k%10==r)
        
            printf("%d\\n",i);
            break;
        
    return 0;

 Problem B-Cormen — The Best Friend Of a Man

Accept: 0    Submit: 0
Time Limit: 1 second    Memory Limit : 256 megabytes

 Problem Description

Recently a dog was bought for Polycarp. The dog's name is Cormen. Now Polycarp has a lot of troubles. For example, Cormen likes going for a walk.

Empirically Polycarp learned that the dog needs at least k walks for any two consecutive days in order to feel good. For example, if k = 5 and yesterday Polycarp went for a walk with Cormen 2 times, today he has to go for a walk at least 3 times.

Polycarp analysed all his affairs over the next n days and made a sequence of n integers a1, a2, ..., an, where ai is the number of times Polycarp will walk with the dog on the i-th day while doing all his affairs (for example, he has to go to a shop, throw out the trash, etc.).

Help Polycarp determine the minimum number of walks he needs to do additionaly in the next n days so that Cormen will feel good during all the n days. You can assume that on the day before the first day and on the day after the n-th day Polycarp will go for a walk with Cormen exactly k times.

Write a program that will find the minumum number of additional walks and the appropriate schedule — the sequence of integers b1, b2, ..., bn (bi ≥ ai), where bi means the total number of walks with the dog on the i-th day.

 Input

The first line contains two integers n and k (1 ≤ n, k ≤ 500) — the number of days and the minimum number of walks with Cormen for any two consecutive days.

The second line contains integers a1, a2, ..., an (0 ≤ ai ≤ 500) — the number of walks with Cormen on the i-th day which Polycarp has already planned.

 Output

In the first line print the smallest number of additional walks that Polycarp should do during the next n days so that Cormen will feel good during all days.

In the second line print n integers b1, b2, ..., bn, where bi — the total number of walks on the i-th day according to the found solutions (ai ≤ bi for all i from 1 to n). If there are multiple solutions, print any of them.

 Sample Input

3 5
2 0 1
3 1
0 0 0
4 6
2 4 3 5

 Sample Output

4
2 3 2
1
0 1 0
0
2 4 3 5

 Problem Idea

解题思路:

【题意】

给你一个数组a:a1,a2,...,an

要求任意相邻两项之和不小于k,即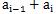≥k

故需要改变数组a中的某些项,使得上述条件成立

问数组a总体至少需要增加多少才能使上述条件成立,并输出改变后的数组b

【类型】
小思维
【分析】

要想总体增加的尽可能少,从上图中显然可以发现,改变中间的那个数更优

因为当我改变ai的值时,可以使得和都变大

而如果改变的是边界上的数,那么就只能增加一个了

【时间复杂度&&优化】
O(n)

题目链接→Codeforces Problem 732B Cormen — The Best Friend Of a Man

 Source Code

/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 505;
const int M = 100005;
const int inf = 1000000007;
const int mod = 1000000007;
int s[N];
int main()

    int n,k,i,ans=0;
    scanf("%d%d",&n,&k);
    for(i=1;i<=n;i++)
        scanf("%d",&s[i]);
    for(i=2;i<=n;i++)
        if(s[i]+s[i-1]<k)
        
            ans+=k-s[i]-s[i-1];
            s[i]=k-s[i-1];
        
    printf("%d\\n",ans);
    for(i=1;i<=n;i++)
        printf("%d%c",s[i],i!=n?' ':'\\n');
    return 0;

 Problem C-Sanatorium

Accept: 0    Submit: 0
Time Limit: 1 second    Memory Limit : 256 megabytes

 Problem Description

Vasiliy spent his vacation in a sanatorium, came back and found that he completely forgot details of his vacation!

Every day there was a breakfast, a dinner and a supper in a dining room of the sanatorium (of course, in this order). The only thing that Vasiliy has now is a card from the dining room contaning notes how many times he had a breakfast, a dinner and a supper (thus, the card contains three integers). Vasiliy could sometimes have missed some meal, for example, he could have had a breakfast and a supper, but a dinner, or, probably, at some days he haven't been at the dining room at all.

Vasiliy doesn't remember what was the time of the day when he arrived to sanatorium (before breakfast, before dinner, before supper or after supper), and the time when he left it (before breakfast, before dinner, before supper or after supper). So he considers any of these options. After Vasiliy arrived to the sanatorium, he was there all the time until he left. Please note, that it's possible that Vasiliy left the sanatorium on the same day he arrived.

According to the notes in the card, help Vasiliy determine the minimum number of meals in the dining room that he could have missed. We shouldn't count as missed meals on the arrival day before Vasiliy's arrival and meals on the departure day after he left.

 Input

The only line contains three integers b, d and s (0 ≤ b, d, s ≤ 10^18,  b + d + s ≥ 1) — the number of breakfasts, dinners and suppers which Vasiliy had during his vacation in the sanatorium.

 Output

Print single integer — the minimum possible number of meals which Vasiliy could have missed during his vacation.

 Sample Input

3 2 1
1 0 0
1 1 1
1000000000000000000 0 1000000000000000000

 Sample Output

1
0
0
999999999999999999

 Hint

In the first sample, Vasiliy could have missed one supper, for example, in case he have arrived before breakfast, have been in the sanatorium for two days (including the day of arrival) and then have left after breakfast on the third day.

In the second sample, Vasiliy could have arrived before breakfast, have had it, and immediately have left the sanatorium, not missing any meal.

In the third sample, Vasiliy could have been in the sanatorium for one day, not missing any meal.

 Problem Idea

解题思路:

【题意】

Vasiliy从住进疗养院到离开,一共吃了b顿早饭,d顿午饭和s顿晚饭(有时候他会因为某些原因错过几顿饭)

问Vasiliy最少错过几顿饭

【类型】
思维
【分析】

本题之所以有最少这么一说,是因为Vasiliy不管早饭、午饭还是晚饭,都有可能错过,那如果三个时间段的饭都错过了,就不好确定到底错过多少顿

故有最少这一说,也就是让我们把吃的最多的一个时间段的饭当作没有错过

此外,我们可以确定的是,不管Vasiliy入住的时间和离开的时间到底是哪个时间段,三个时间段的饭吃的次数最多相差一次

共有以下九种情况:

三餐次数	早	中	晚
早	n/n/n	n+1/n/n	n+1/n+1/n
中	n-1/n/n	n/n/n	n/n+1/n
晚	n-1/n-1/n	n/n-1/n	n/n/n

由上表就可以清楚地得到结论:三个时间段的饭吃的次数最多相差一次

故我们只需取出三餐中吃的次数最多的一餐作为基准,求一下少了几次即可

【时间复杂度&&优化】
O(1)

题目链接→Codeforces Problem 732C Sanatorium

 Source Code

/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 505;
const int M = 100005;
const int inf = 1000000007;
const int mod = 1000000007;
int main()

    __int64 b,d,s,Max,ans=0;
    scanf("%I64d%I64d%I64d",&b,&d,&s);
    Max=max(max(b,d),s)-1;
    if(b<Max)
        ans+=Max-b;
    if(d<Max)
        ans+=Max-d;
    if(s<Max)
        ans+=Max-s;
    printf("%I64d\\n",ans);
    return 0;

 Problem D-Exams

Accept: 0    Submit: 0
Time Limit: 1 second    Memory Limit : 256 megabytes

 Problem Description

Vasiliy has an exam period which will continue for n days. He has to pass exams on m subjects. Subjects are numbered from 1 to m.

About every day we know exam for which one of m subjects can be passed on that day. Perhaps, some day you can't pass any exam. It is not allowed to pass more than one exam on any day.

On each day Vasiliy can either pass the exam of that day (it takes the whole day) or prepare all day for some exam or have a rest.

About each subject Vasiliy know a number ai — the number of days he should prepare to pass the exam number i. Vasiliy can switch subjects while preparing for exams, it is not necessary to prepare continuously during ai days for the exam number i. He can mix the order of preparation for exams in any way.

Your task is to determine the minimum number of days in which Vasiliy can pass all exams, or determine that it is impossible. Each exam should be passed exactly one time.

 Input

The first line contains two integers n and m (1 ≤ n, m ≤ 10^5) — the number of days in the exam period and the number of subjects.

The second line contains n integers d1, d2, ..., dn (0 ≤ di ≤ m), where di is the number of subject, the exam of which can be passed on the day number i. If di equals 0, it is not allowed to pass any exams on the day number i.

The third line contains m positive integers a1, a2, ..., am (1 ≤ ai ≤ 10^5), where ai is the number of days that are needed to prepare before passing the exam on the subject i.

 Output

Print one integer — the minimum number of days in which Vasiliy can pass all exams. If it is impossible, print -1.

 Sample Input

7 2
0 1 0 2 1 0 2
2 1
10 3
0 0 1 2 3 0 2 0 1 2
1 1 4
5 1
1 1 1 1 1
5

 Sample Output

5
9
-1

 Hint

In the first example Vasiliy can behave as follows. On the first and the second day he can prepare for the exam number 1 and pass it on the fifth day, prepare for the exam number 2 on the third day and pass it on the fourth day.

In the second example Vasiliy should prepare for the exam number 3 during the first four days and pass it on the fifth day. Then on the sixth day he should prepare for the exam number 2 and then pass it on the seventh day. After that he needs to prepare for the exam number 1 on the eighth day and pass it on the ninth day.

In the third example Vasiliy can't pass the only exam because he hasn't anough time to prepare for it.

 Problem Idea

解题思路:

【题意】

考试期有n天,有m门学科要考试

Vasiliy准备第i门学科的考试总共需要ai天

现给你考试期内每天的考试安排,问Vasiliy最少需要几天能把所有学科的考试考完

【类型】
二分答案+贪心
【分析】

对于此题,如果直接贪心安排每天要准备哪门考试还是有点麻烦的

故采取了二分答案的策略

即二分Vasiliy能够考完所有学科的时间t,再判断这个时间能不能完成所有考试

而判断的方法也相对简单

保留1~t天内每门学科最后一次的考试时间,其余时间用来准备考试

当某门考试时间到来时,只需判定当前还剩余的复习时间是否足够就可以了

【时间复杂度&&优化】
O(M·logN)

题目链接→Codeforces Problem 732D Exams

 Source Code

/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 100005;
const int M = 100005;
const int inf = 1000000007;
const int mod = 1000000007;
int d[N],a[N],s[N],m;
bool v[N];
bool judge(int x)

    int i,day=0;
    memset(v,false,sizeof(v));
    for(i=x;i>=1;i--)//保留1~x天内每门学科最后的一次考试时间
        if(!v[d[i]])
        
            v[d[i]]=true;
            s[i]=d[i];
        
        else
            s[i]=0;
    for(i=1;i<=m;i++)//1~x天内是否还有学科未安排考试
        if(!v[i])
            return false;
    for(i=1;i<=x;i++)
        if(s[i])
        
            if(day<a[s[i]])//考试时,剩余的复习时间不够准备该考试
                return false;
            day-=a[s[i]];
        
        else
            day++;
    return true;

int main()

    int n,i,l,r,mid,ans=inf;
    scanf("%d%d",&n,&m);
    for(i=1;i<=n;i++)
        scanf("%d",&d[i]);
    for(i=1;i<=m;i++)
        scanf("%d",&a[i]);
    l=1;r=n;
    while(l<=r)//二分能够考完所有学科的时间
    
        mid=(l+r)/2;
        if(judge(mid))
            r=mid-1,ans=min(ans,mid);
        else
            l=mid+1;
    
    if(ans!=inf)
        printf("%d\\n",ans);
    else
        puts("-1");
    return 0;

菜鸟成长记