数据结构与算法:图

Posted 史大拿

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构与算法:图相关的知识，希望对你有一定的参考价值。

Tips: 采用java语言,关注博主,底部附有完整代码

工具:IDEA

本篇介绍的是数据结构: 图

更多数据结构请转至偶的主页

什么是图

图是一种比较复杂的非线形数据结构

非线形数据结构有2种:

  • 树
  • 图

如果想参考树,点击连接即可

虽说树和图都是非线形结构,但是他们也有说区别:

一般常见的二叉树只有2个结点,并且他们是有父子关系的.“等级制度”比较森严

但是图则不同,图都是平级的,没有父子之分,并且1个图结点之间可以有多个图结点相连接

常见的图有很多种,例如地铁路线:

这个图比较复杂,先来看一张简单的图:

图由2种东西组成:

  • 顶点[vertex] (我喜欢叫图结点)

  • 边 [edge]

图还分方向,是否环绕,一般有:

无向无环图无向有环图有向有环图有向无环图

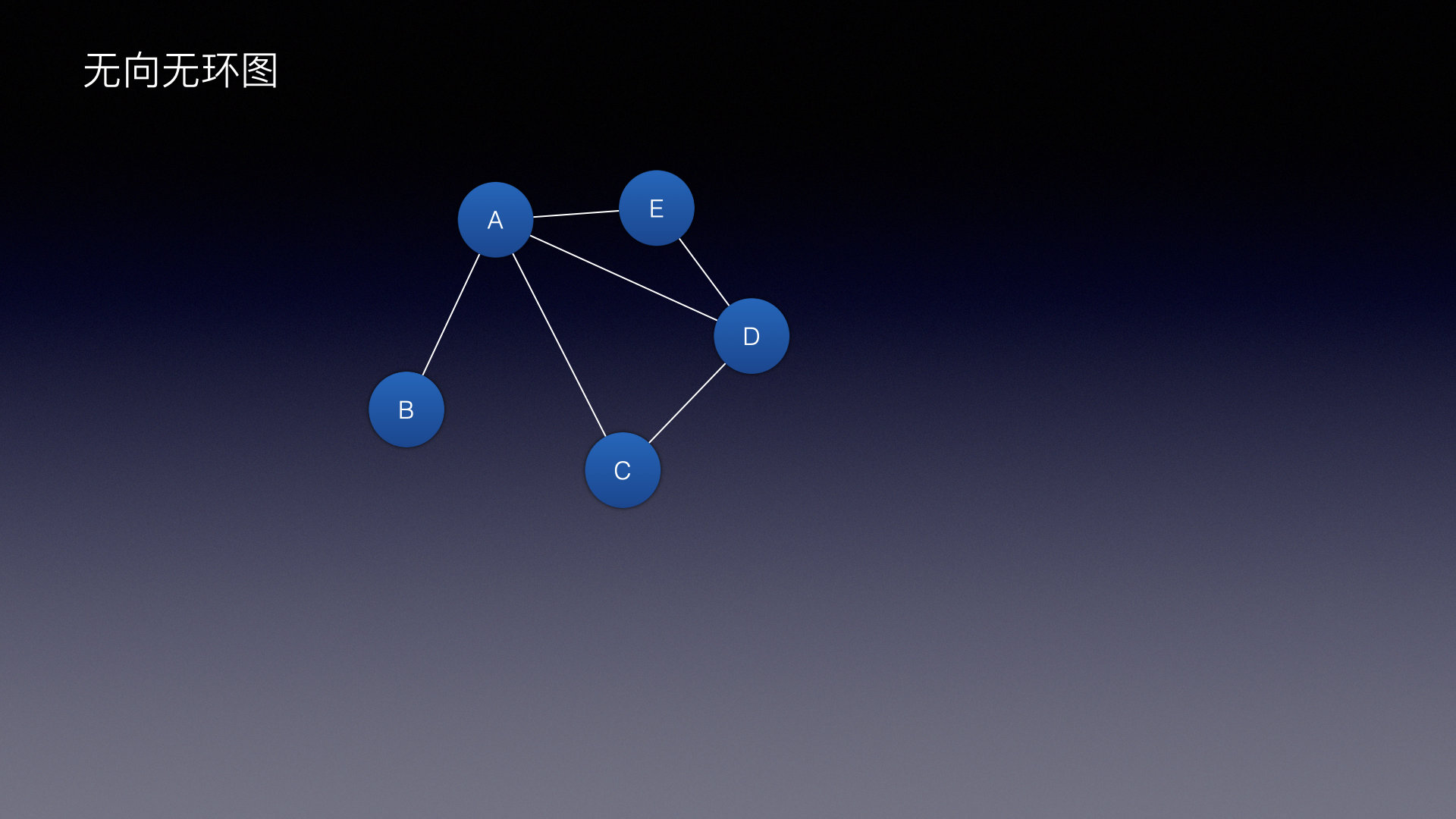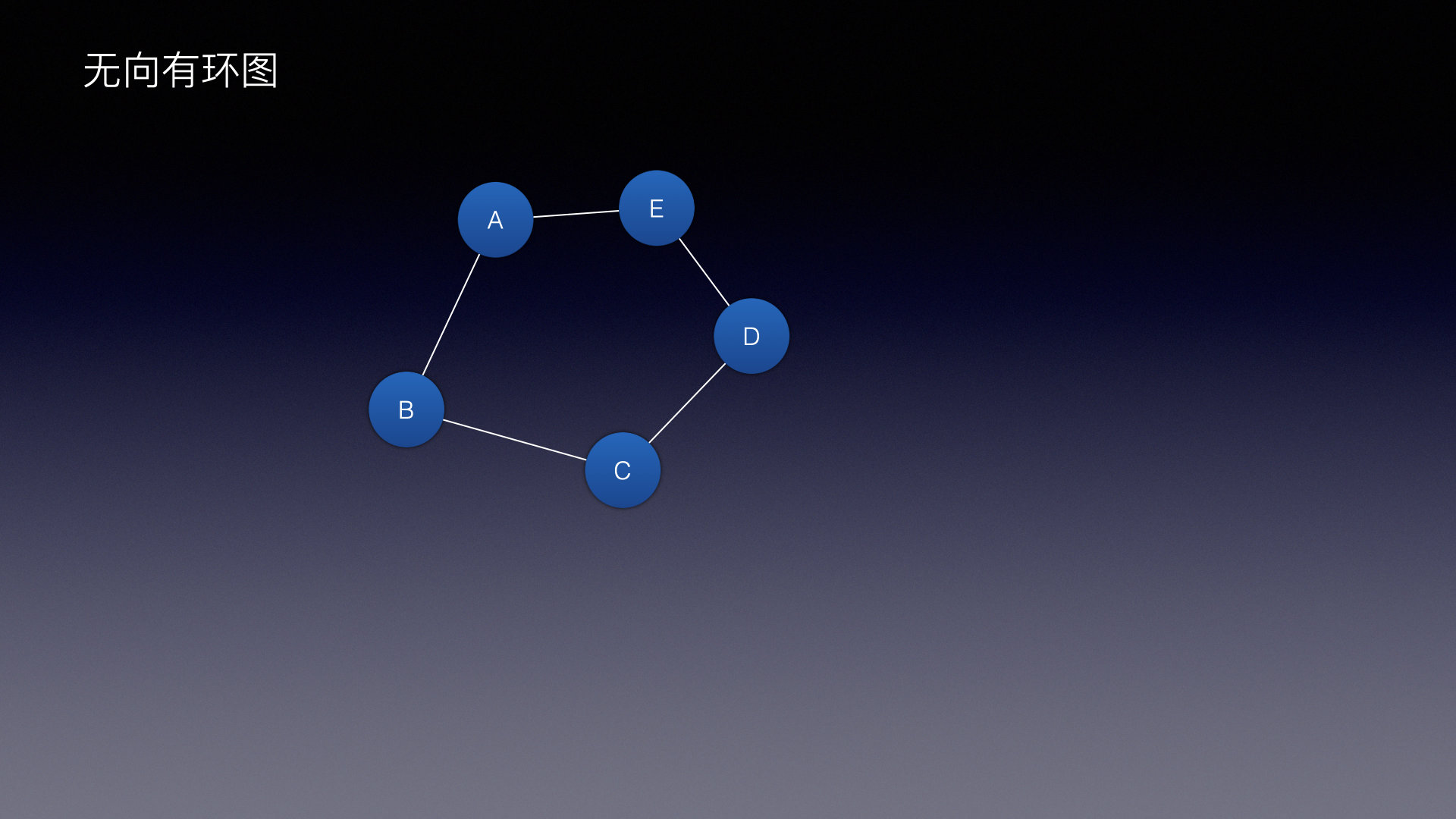  • 向: 指的就是方向

  • 环: 指的就是是否环绕

图的输出方式

图的显示方式有2种

  • 邻接矩阵
  • 邻接链表

以无向无环图为例:

邻接矩阵:

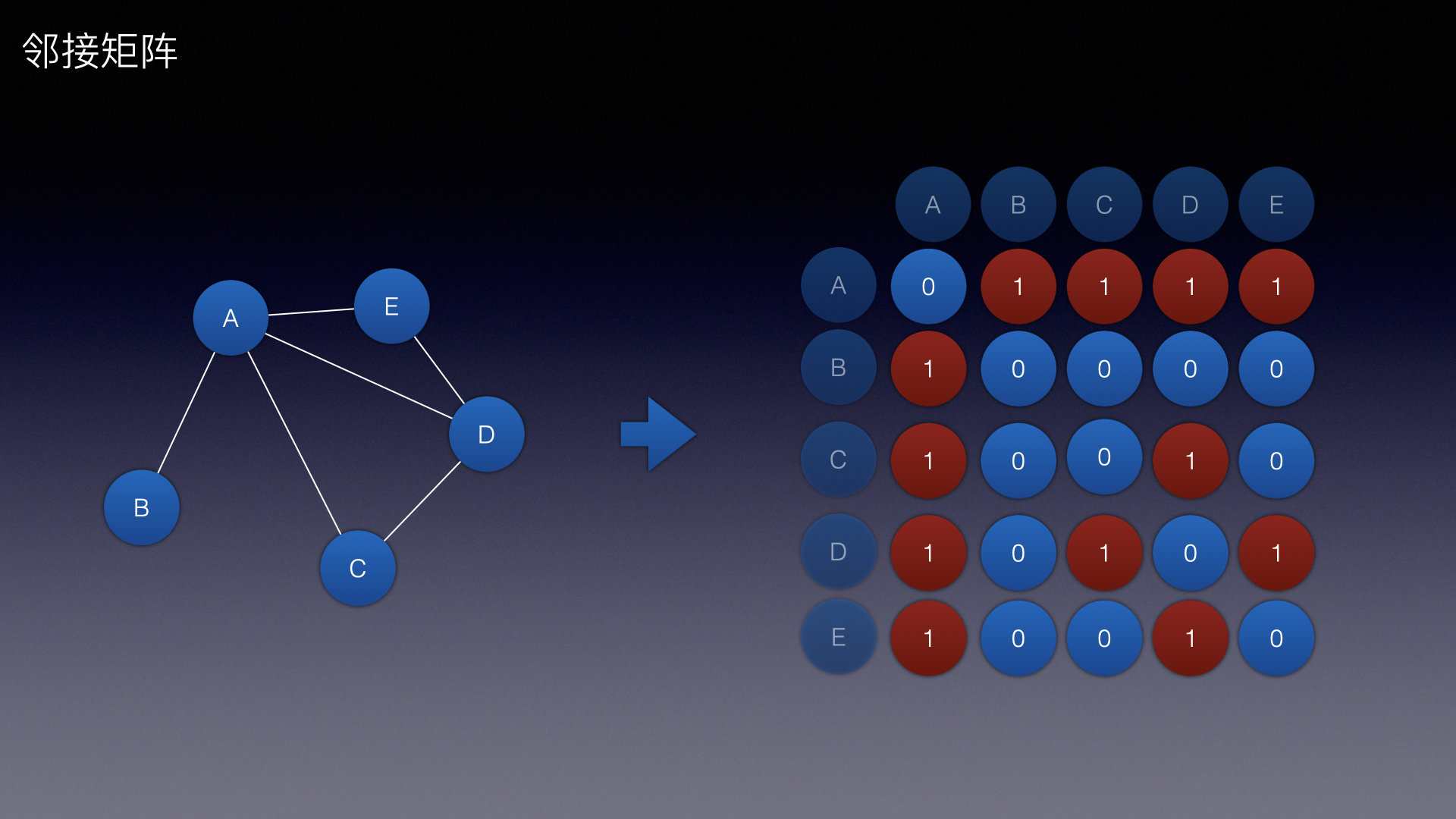
  • 用1表示他们相连接

  • 用0表示他们未连接

因为他是无向无环图,所以CD如果相连,那么DC就一定相连接

等价换算到矩阵中,(2,3)如果是1,那么(3,2)一定是1

邻接链表:

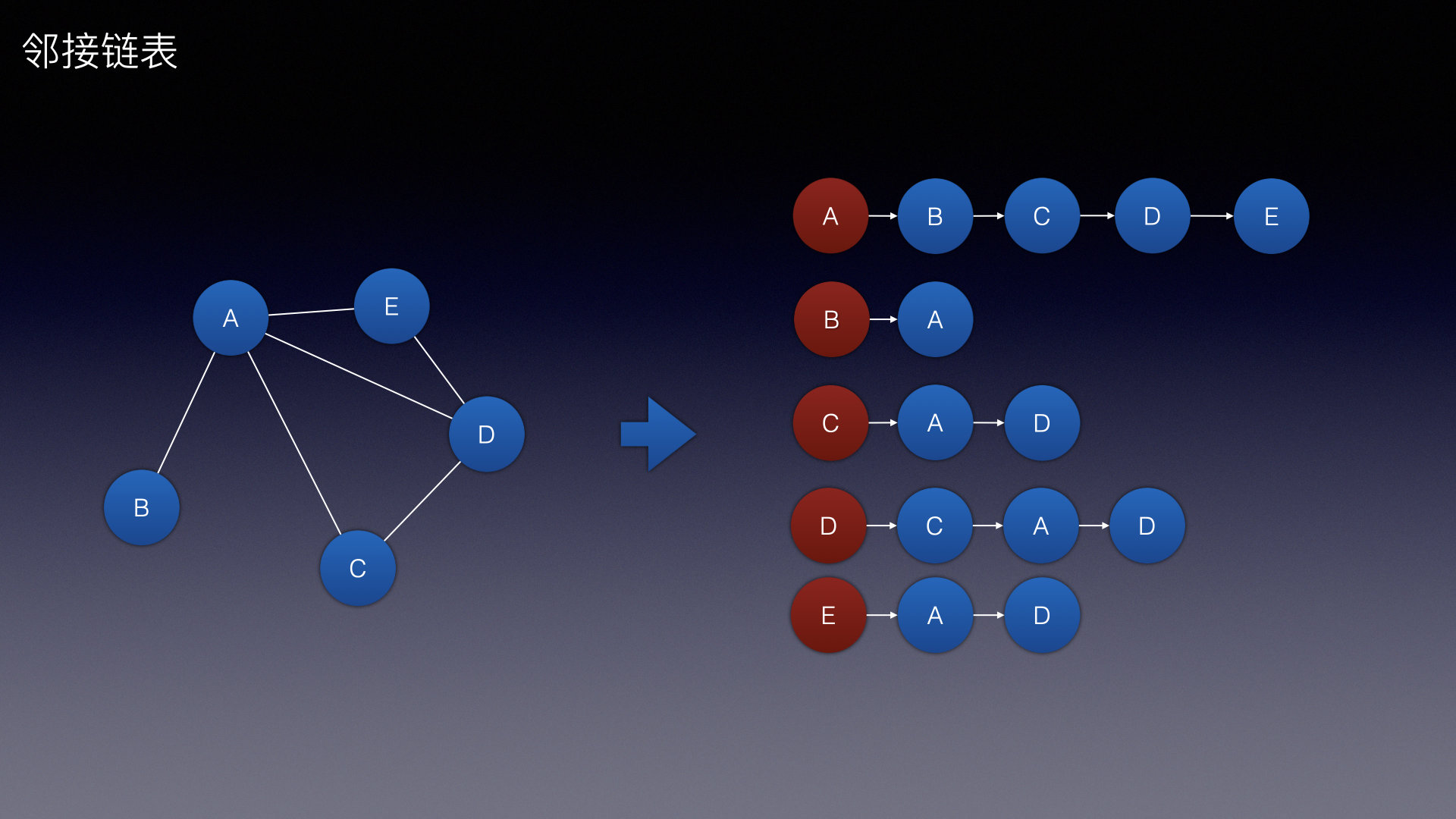
通过链表的形式展示

以A顶点为例

用链表展示为A -> B -> C -> D -> E

表示:

  • A和B
  • A和C
  • A和D
  • A和E

连接

创建一张图

创建图之前首先需要创建一个图顶点(结点):

public static class GraphNode 

    // 顶点
    String value;

    public GraphNode(String value) 
        this.value = value;
    

    @Override
    public String toString() 
        return "value='" + value;

创建图,添加顶点添加边:

代码比较简单,就直接看了,后面广度优先遍历深度优先遍历在细聊!

采用邻接矩阵的方式打印图:

public class Graph 

    // 用来存放顶点
    private GraphNode[] graphNodes;
  
  	// 矩阵
    private int[][] matrix;
  
    // 存放顶点个数
    private int maxSize;
  
    // 记录当前存放位置
    private int currentIndex;
  
    public Graph(int size) 
        maxSize = size;
        graphNodes = new GraphNode[maxSize];
        matrix = new int[maxSize][maxSize];
    
  
     // 顶点是否存在
    public int containsVertex(String vertex) 
        for (int i = 0; i < graphNodes.length; i++) 
            if (graphNodes[i].value.equals(vertex)) 
                return i;
            
        
        return -1;
    

    // 是否存放满     
    public boolean isFull() 
        return graphNodes.length >= currentIndex;
    
  
  	// 添加顶点
    public void addVertex(GraphNode node) 
      if (isFull()) 
         graphNodes[currentIndex++] = node;
       else 
         throw new RuntimeException("存满了,只能存放" + maxSize + "个顶点");
      
    
  
  	// 添加边
  	public void addEdge(String ver1, String ver2) 
        // 顶点1下标
        int ver1Index = containsVertex(ver1);
        // 顶尖2下标
        int ver2Index = containsVertex(ver2);

        // 如果顶点1 和顶点2 都存在
        if (ver1Index != -1 && ver2Index != -1) 
            // 无向无环图 直接两端连接即可
            matrix[ver1Index][ver2Index] = 1;
            matrix[ver2Index][ver1Index] = 1;
         else 
            System.out.println("边添加失败");
        
    
  
  	// 顶点是否存在
  	public int containsVertex(String vertex) 
        for (int i = 0; i < graphNodes.length; i++) 
            if (graphNodes[i].value.equals(vertex)) 
                return i;
            
        
        return -1;
    
  
   // 打印数据
  public void show() 
        System.out.print("\\t");
        // 打印顶点
        for (GraphNode graphNode : graphNodes) 
            System.out.printf("%s\\t", graphNode.value);
        
        System.out.println();

        // 打印边
        for (int i = 0; i < matrix.length; i++) 
            for (int j = 0; j < matrix[i].length; j++) 
                if (j == 0) 
                    System.out.printf("%s\\t", graphNodes[i].value);
                
                System.out.printf("%d\\t", matrix[i][j]);
            
            System.out.println();

Graph.java 中 api设计:

属性名作用
GraphNode[] graphNodes;用来存放顶点
int[][][] [] matrix;矩阵
int maxSize;存放最大存储顶点个数
int currentIndex;存放当前添加顶点位置
方法名作用参数介绍
boolean isFull()是否存放满-
void addVertex(GraphNode)添加顶点@param 1:顶点信息
void addEdge(String ver1, String ver2)添加边@param1: 从哪个顶点开始
@param2: 到那个顶点结束
int containsVertex(String vertex)顶点是否存在输入顶点
如果顶点存在,返回对应数组下标,否则返回-1
void show()打印当前数据-

调用:

Graph graph = new Graph(5);

// 添加结点
graph.addVertex(new Graph.GraphNode("A"));
graph.addVertex(new Graph.GraphNode("B"));
graph.addVertex(new Graph.GraphNode("C"));
graph.addVertex(new Graph.GraphNode("D"));
graph.addVertex(new Graph.GraphNode("E"));

// 添加边
graph.addEdge("A", "B");
graph.addEdge("A", "C");
graph.addEdge("A", "D");
graph.addEdge("A", "E");

graph.addEdge("E", "D");

graph.addEdge("D", "C");

graph.show();

结果:

	A	B	C	D	E	
A	0	1	1	1	1	
B	1	0	0	0	0	
C	1	0	0	1	0	
D	1	0	1	0	1	
E	1	0	0	1	0

辅助图:

深度优先(DSF)遍历算法

深度优先遍历(Depth-First-Search) 简称DSF,是图遍历顶点的一种方式

DSF学习重点:

如果是初学者,想搞懂DSF,首先要忘记当前和图有任何关系,

只需要记住对应的矩阵图即可,

现在只是操作的一个二维数组,这个二维数组只有0和1

假设这个二维数组中(2,3)元素为1

那么(3,2)元素也一定为1 !!

辅助图1.0:

先来介绍2个最关键的方法:

  1. 输入第n行,输出第n行为1的位置,如果不存在,则返回-1
public int getFirstNeighbor(int row) 
    for (int column = 0; column < graphNodes.length; column++) 
        // 判断是否存在，如果存在则返回对应的下标
        if (matrix[row][column] == 1) 
            return column;
        
    
    return -1;

以辅助图1.0为例

  • 输入0,得到1, 输入的0表示第0行,得到的1表示在第0行第1个为1的位置在下标为1的地方
  • 输入3得到0, 和上面同理, 3代表行,0代表第3行第一个1的下标位置
  • 输入4得到0 ,同理
  1. 输入第n行,第k列,返回第n行第k列后第一个为1的位置
public int getNextNeighbor(int row, int column) 
    for (int i = column + 1; i < graphNodes.length; i++) 
        // 遍历某一行,返回当前行下标位置
        if (matrix[row][i] == 1) 
            return i;
        
    
    return -1;

row = 1,column = 1, 输出-1,因为(1,1)位置以后全是0

row = 2,column = 1, 输出 3, (2,1) 后第1个1的位置为3

先来看看完整DSF遍历流程:

深度遍历只要记住 是通过行找列,然后在看代码就会简单很多

DSF完整代码:

首先需要在图结点中添加一个变量,标识当前结点是否访问过:

public static class GraphNode 

    // 顶点
    String value;

    // 是否访问过 [默认未访问过]
    boolean isVisited;

    public GraphNode(String value) 
        this.value = value;
    

    @Override
    public String toString() 
        return "value='" + value;

深度优先代码:

/*
 * @author: android 超级兵
 * @create: 2022/7/19 09:52
 * TODO dsf 深度优先遍历
 */
private void showDSF(int i) 
    // 首先我们访问该结点
    System.out.println("深度遍历:" + graphNodes[i].value);
    // 将当前结点设置为已经访问
    graphNodes[i].isVisited = true;

    // 以当前结点进行深度遍历

    // 查找结点i的第一个邻接点是否存在
    int firstNeighbor = getFirstNeighbor(i);
    while (firstNeighbor != -1) 
        // 并且当前结点没有被访问过
        if (!graphNodes[firstNeighbor].isVisited) 
            showDSF(firstNeighbor);
        

        // 如果 firstNeighbor 结点被访问过,去查找下一个邻接点
        firstNeighbor = getNextNeighbor(i, firstNeighbor);
    


// 深度优先
public void showDSF() 
    // 从0开始回溯
    showDSF(0);

广度优先(BSF)遍历算法

广度优先(Breadth first search)简称BSF

百度百科

广度优先完整流程图:

完整代码:

// 广度优先
public void showBSF() 
    showBSF(0);


/*
 * @author: android 超级兵
 * @create: 2022/7/20 13:44
 * TODO 广度优先遍历(BSF broad first search)
 */
private void showBSF(int i) 
    // 表示队列头结点对应的下标
    int u;
    // 邻接点
    int w;
    // 队列 记录结点访问顺序
    Queue<Integer> queue = new LinkedList<>();

    System.out.println("广度遍历1:" + graphNodes[i].value);
    // 设置已访问过
    graphNodes[i].isVisited = true;
    queue.add(i);

    // 队列 != null
    while (!queue.isEmpty()) 
        u = queue.poll();

        // 得到第一个邻接点的下标
        w = getFirstNeighbor(u);

        while (w != -1) 
            // 找到了结点

            // 没有访问过
            if (!graphNodes[w].isVisited) 
                System.out.println("广度遍历2:" + graphNodes[w].value);
                graphNodes[w].isVisited = true;

                // 入队列
                queue.add(w);
            

            // 已经访问过了,找w的后一个邻接点
            w = getNextNeighbor(u, w);

深度优先和广度优先的区别

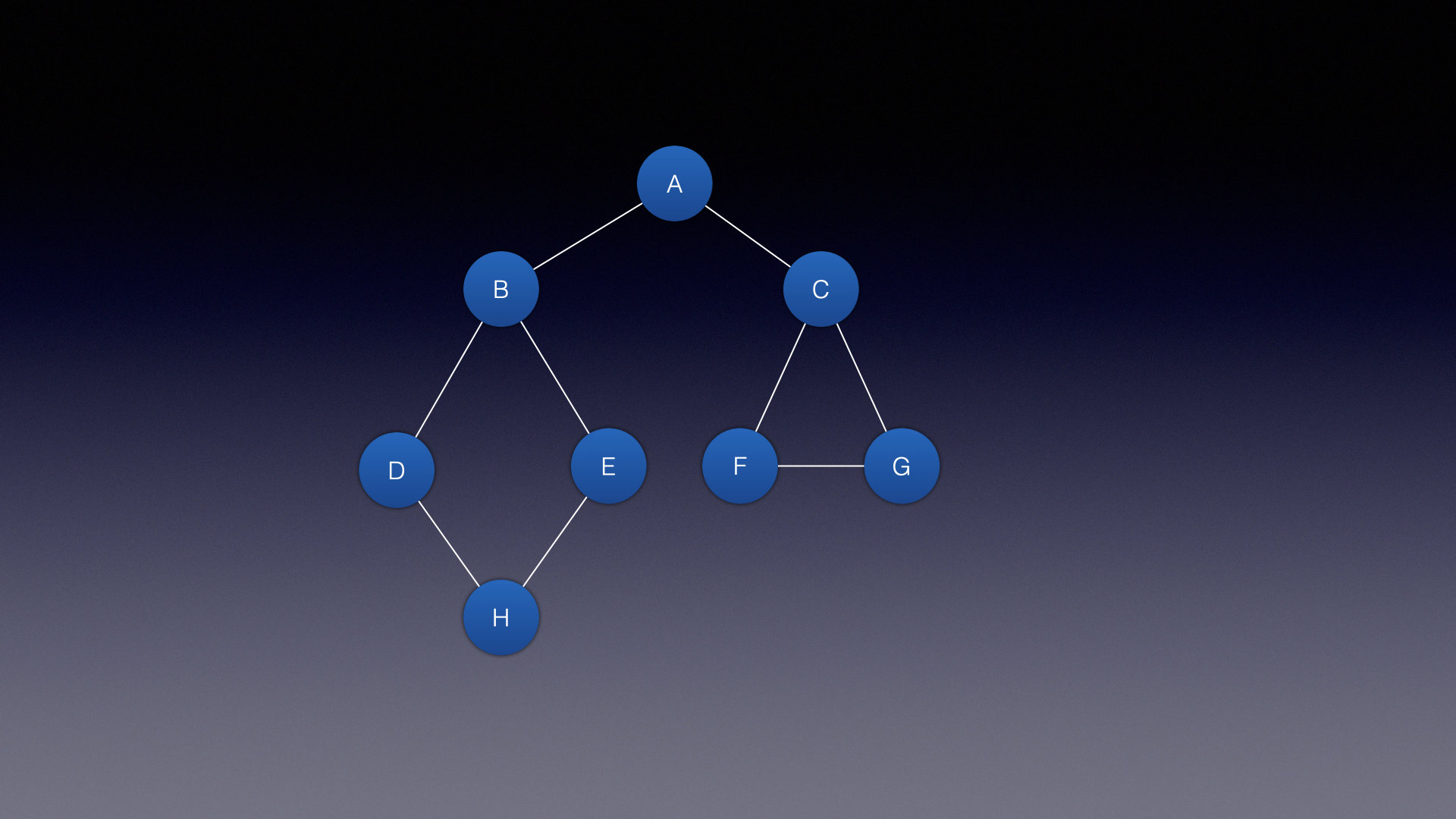
假如现在图结构是这样子

如果是深度优先遍历则顺序为: A->B -> D -> H -> E -> C -> F -> G

如果是广度优先遍历则顺序为: A->B -> C -> D -> E -> F -> G -> H

以这种图结构来说

  • 深度遍历更像是树的前序遍历
  • 广度遍历更像是树的层序遍历

通过名字也可以看出,深度是先抄底,然后再依次遍历

广度就是一层一层遍历.

本篇到此结束!

心得: 感觉本篇和树的文章来比写的不太好,可能是因为图用的比较少, 并且DSF和BSF 难度大了一点比较急躁.

在后面的学习过程中还是得静下来… -.-!

完整代码

您的点赞就是对我最大的支持!

以上是关于数据结构与算法:图的主要内容，如果未能解决你的问题，请参考以下文章

【tableau数据分析可视化-专题（5）】-Tableau制作线形图

plotly基于dataframe数据绘制线形图（line plot）

Charts：一个强大的iOS图表框架

七大查找算法

7种查找算法详解（转）

JFreeChart线形图的简单应用