高精度点云配准（最优传输角度下篇）

Posted 2022-07-28 等待破茧

转载自高精度点云配准（最优传输角度下篇） - 知乎

这里还是分成两篇写。相对于上篇而言， 下篇更侧重于给出在不同任务场景下的一些解决方案， 这里会尽可能的提供范化的解决思路。 当然这些都是启发式的，相信在最优传输 optimal transport的特性被业界熟知后，会有更多精彩的工作。

这里还是强调一下， 如果对最优传输的在点云配准中的特性还不熟悉的同学强烈建议先阅读上篇后再阅读此文。

回归正题这里我们主要讨论高精度点云配准。

整体文章结构如下，因为是下篇，所以我们讨论第三和第四部分

1. 点云配准的现状
2. 最优传输简介
3. 形变模型（deformation model）
4. 高精度点云配准

第三部分：形变模型（deformation model）

这部分我们会简单的提及下几个典型的形变模型和它们的一些特点。

所以为什么要引入形变模型呢， 回到上次那个任务，如果只用xyz作为每个点的特征，在没有引入对transformation 的regularization 情况下，RobOT 虽然几毫秒就可以完成transfrom， 但效果并不好。

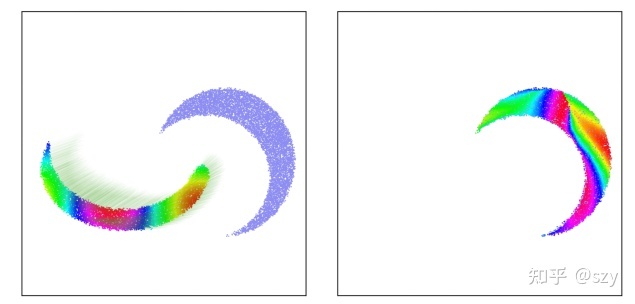
Fig3.1, registration via RobOT. Please refer to Figure 3.31, F. Jean, Geometric data analysis, beyond convolution, 2021

这里我们可以先看下传统模型的表现。

Fig 3.2. Registration via deformation model. Please refer to Figure 4.6, F. Jean, Geometric data analysis, beyond convolution, 2021

这里我们用了一个deformation model 来迭代优化deformed 的形状和target形状间的similarity loss。（具体而言使用的是流体形变模型LDDMM，并在每一步迭代时利用了wasserstein distance，最优传输下的整体cost， 作为similarity loss）。效果看上去是不是挺好的？是挺好的，就是太慢了。可能需要反复迭代几十次，好多秒。

*LDDMM 可以参考我之前写过的流体配准的文章

这里就出来了一个思路，怎么去结合RobOT的速度和传统deformation 的regularization。

再继续讨论这个问题前，我们还是先将目光放在本节的重点deformation model上。deformation model 大致可以分为两类, low dimension parametric model, 像是 rigid (6D) 和 affine (12D), 以及 non-parametric（or free-form) model (可以理解为每个点都有自由度）。

rigid 和 affine 都很直观，也有大量的工作， 这里我们着重强调 non-parametric 部分。这里non-parametric model 里 我们通常用的是位移模型（用的最多，计算对应点位移差，但通常不能保证变换平滑），弹性模型比如spline， 和流体模型比如 LDDMM。

Fig 3.3. Registration from sphere to cube via spline (below) and LDDMM(above), respectively.

这里有一个 sphere (source) 到 cube(target) 的例子，可以看到用spline 和 LDDMM 模型配准的结果都体现了一定的regularization， 但LDDMM对sharp edge的还原度更高。

总结一些的话， 不同场景下deformation model的选择也决定了最终transformation 的性质，一般而言，小形变的话，spline 模型就够用了，大形变LDDMM通常效果更好。不同的问题要选择适当的形变模型， 像月亮匹配那个这个问题，如果用rigid模型作为underlying 形变模型的话更合适。

另外从求解效率角度， 如果给定了source 和 target set 中的对应点，rigid， affine， spline都是有closed form 的解的（求解会非常快）。具体可以参考这文章里的第三节。LDDMM即使存在点对点的对应关系也需要迭代求解，但这时每次迭代时的similarity loss 就是简单的L2 了， 求解速度会对比计算 set to set distance时大大加快。正如我们之前提到过，这里启发了我们可以用RobOT先得到source to target 的点对点对应，再求解（映射）选定的deformation model来得到regularized transformation。我们会再下一节中具体这个思路。

第四部分： 高精度点云配准

下面我们会讨论如何融合RobOT 和deformation model来得到可靠精确的解。

提前申明本节讨论的方法适用于：

• 刚性变换（可以是paritial 的)
• 没有很大occlusion前提下的自由变换（non-parametric transformation)

*至于其他情形，比如大occlusion的情形，希望之后可以看到和occlusion mask 结合的工作。

回到正题，对于高精度点云配准， 这里有两个思路，分别是针对两种比较常见的任务类型。 1. 在特征已经提取好的前提下，匹配两个点云。 2. 没有特征，直接通过端到端的深度学习模型去匹配点云。

第一个更接近传统的方式，对feature engineering 的要求比较高，这里feature matching 和transformation的计算是独立的。第二个是近期学术界比较流行的，端到端的话省去了handcrafted feature design的过程。

现在趋势而言，类型2端到端的进行配准确实更具有吸引力，毕竟省去了explicit的特征提取模块，同时在数据量足够多的情形下，效果很多时候也胜于单独提取特征再配准的效果。 但正如这里强调的，训练端到端深度模型的话数据规模很重要，另外测试场景也必须不能和训练场景差别太大。

相对而言，类型1 中如果将特征学习任务独立于配准任务，虽然配准的准确率上可能比不上端到端，但这个策略依旧非常重要。为什么呢，这里总结两点 1）很多经典的handcrafted feature, 像是FPFH， 并不需要大数据支持，可以很容易地自己或调取第三方实现， 只要feature matching的模型设计的合适，配准的效果就可能做到很好。 2）在很多数据分析领域， 特征本身是非常具有吸引力，会被用到各种场景中，比如在做population analysis的时候，特征的聚类和可视化是非常重要的任务。这时即使没有很好的handcrafted feature, 往往也可以通过self-supervised 的方法学到有价值的特征（一般而言，表达力适中的特征对数据量的要求并不是很大）。在学到这些特征后，我们可以将其用于各种上游任务，其中包括配准。

这里我们针对两个任务各自提出一个高效的解决方案。

*虽然这里标题用的是高精度，但从现有的结果来严格讨论，没有加入后期处理的方案1现阶段并不完美，只有端到端的方案2才可以称得上高精度。

方案一： 基于特征，求解transformation

对应之前的例子， 我们曾讨论过， 得益于OT求解效率质的提升，RobOT求解点云配准的效率非常高百万级别的点云匹配都可以再一秒内完成，但它的transformation 不够smooth。另一个角度，传统的deformation model得到的结果可能比较合理，但毕竟在不知道source 和target点对点对应关系的情况下，每一步不论是计算chamfer distance( ICP 用的） 还是 wasserstein distance(OT用的）都非常的消耗算力。 结合两者的优缺点，这里的一个思路就是先对每个点提取适当的特征，利用RobOT得到一个初步合理（可能是non-smooth） 的transformation map，这之后再将其投射到smooth 的deformation model 的space上（用deformation model 去拟合RobOT的结果）。我们称这个方法为 Smooth-RobOT （S-RobOT）。

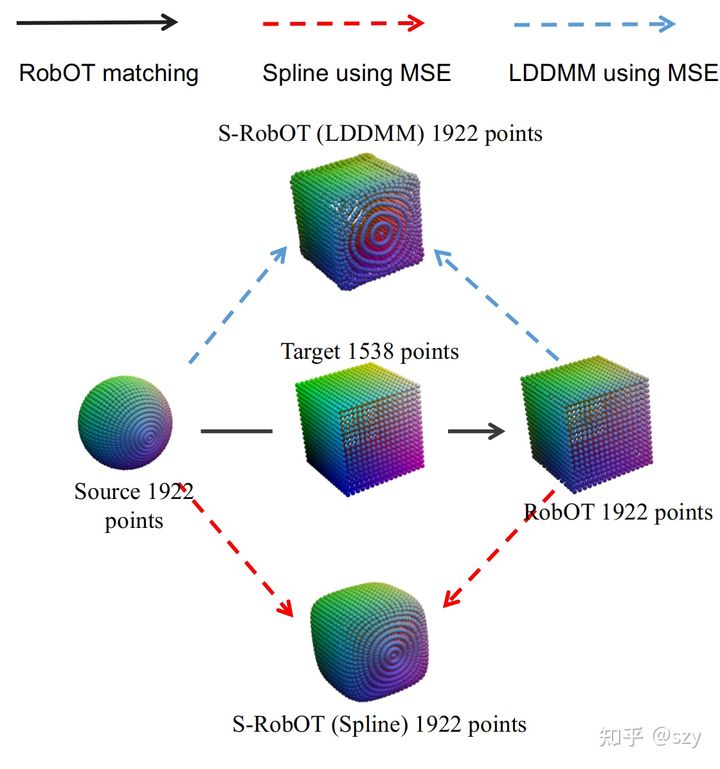
Fig.4.1. Registration via spline-based Smooth-RobOT (below) and LDDMM-based Smooth-RobOT(above).

这里我们还是用了sphere to cube 的简单例子。因为是验证概念用的例子，比较简单所以我们这里直接用xyz作为作为每一个点的特征，我们可以看到source 在对target用RobOT matching 之后，得到了一个相似于target 但和source 存在一一对应点的deformed shape。利用这个RobOT matching 的结果， 我们可以利用closed form 直接求出spline deformation的解，同样的我们可以利用点对点的L2 loss 快速迭代求解LDDMM， 我们看到这里我们对spline 和 LDDMM的求解结果和 Fig.3.3 中用deformation model 和set to set distance 的结果基本一致，但在速度上远胜。

我们再看一个更复杂的例子。我们想要匹配一对肺部树桩血管 （吸气到呼气）。这个任务的难度是肉眼可见的大。这里我们采用了一样的步骤 1.feature extraction 2. RobOT 3. Spline-based Smooth-RobOT.

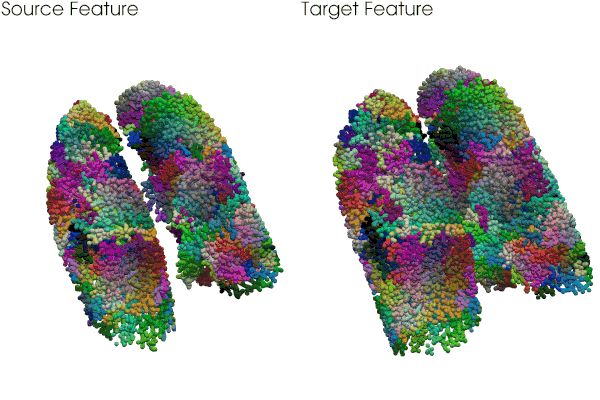
Fig 4.2 TSNE visualization of lung point feature.

比较特别是，一般的特征在这个任务中难挑大担，所以我们采用了self-supervised learning 的手段。这个方法本身的思路和实现还是很有意思的，内容局限有兴趣的同学就请参考文章A3.3 吧。

下一步就是 RobOT 和Spline投影了，这里有source ,target 各有六万点，在程序没有精简的情况下，大约需要2s多跑完从特征提取到最后的transformation求解。

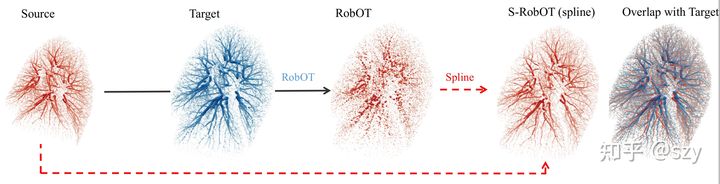
Fig.4.3. S-RobOT(spline) on lung vessel tree registration.

可以看到在RobOT 阶段求解出的transformation比较noisy，但在spline projection后就平滑了好多。

但效果上我们看到虽然deformed source 和target 很接近了，但并不完美。这里我们讨论下第二种端到端解决方案来得到更高精度的配准结果。

方法二： 端到端求解transformation

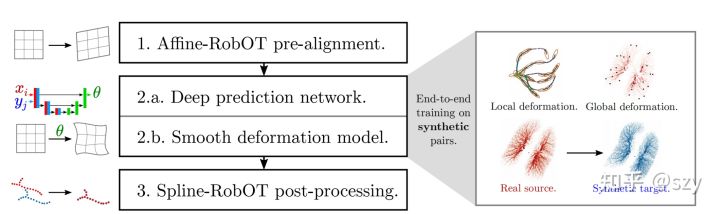
Fig.4.4. Deep RobOT pipeline.

端到端这个概念在CV 界是真的火，因为这个确实大大简化了任务的拼接难度。这里我们同样采用了端到端的思想，输入source set 和 target set 得到它们间的transformation, 但并不是完全的端到端，为什么这么说呢？ 因为我们还加入了非deep learning based 前置预处理模块和后置finetune 模块。这两个模块都是基于RobOT所以速度在毫秒级，并不影响整体的速度。总体而言，我们用了一个预处理模块（optimiatzion-based）， deep non-parametric 模块（支持多种deformation model，deep-learning based), 后处理模块（optimization-baed) 的三明治结构。我们称这个方法为 Deep-RobOT(D-RobOT)

至于为什么这么设计呢。 三个模块对应三个原因 1）为什么加入预处理，一般而言大部分non-parametric模型都是针对与局部形变设计的regularization，需要预先移除全局translation，rotation, shear 和 scale。 2）为什么采用non-parametric， 局部形变的处理需要non-parametric 模型，另外通过任务类型可以选择相应的模型， 像场景流这类型小形变任务，control point based spline model 能求解平滑的流场，对比full resolution 的位移场，spline 的结果一般更平滑， 另外control point 的引入可以大大降低计算内存消耗。 3）为什么采用 后处理， 这是因为不要过分的依赖深度模型，很多时候模型可能并不会给出完美的结果，这时候后处理可以修正模型误差。

Fig.4.5. D-RobOT registration results on lung vessel tree pair registration.

这里同样我们采用了肺部点云配准的例子，我们可以看到经过预处理， deep 配准和后处理，得到的transformed 结果比较完美。

有同学可能会问，source 和 target 肺部点云之间没有对应关系，你怎么训练深度模型。这是一个很重要的问题。 我们发现一个通用的解决方案就是数据生成： 通过尽可能真实的deform source 来得到一个deformed source 作为 pseudo target， 这样训练的时候就可以有一一对应的关系了。 更多利用这种synthesized supervised loss 还是 real unsupervised loss 的讨论可以参见文章A.4.2。 那不可避免的domain gap 怎么办啊，别忘了后处理模块，一般情况下它能够有效处理gap。

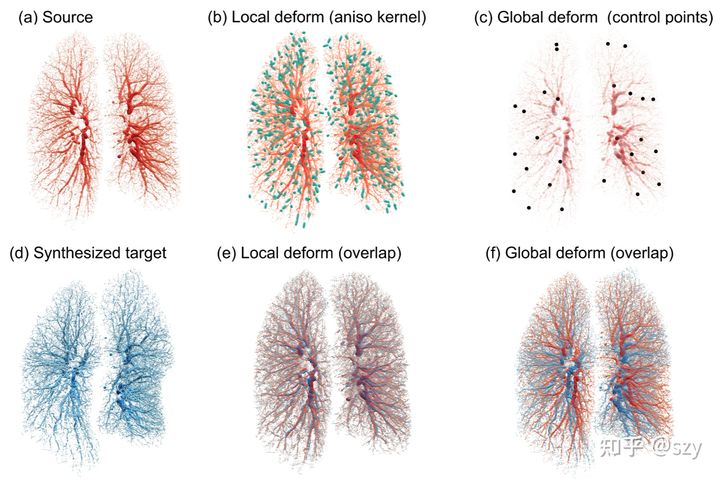
Fig.4.6. lung vessel tree synthesized training pair.

以肺部点云配准为例，这里我们用了局部形变和全局形变来deform source生成pseudo target.这样我们就得到了一组存在ground flow 的training pair。

最后，我们再看一个场景流的例子并顺带讨论下D-RobOT 对比RobOT 的一些性质。

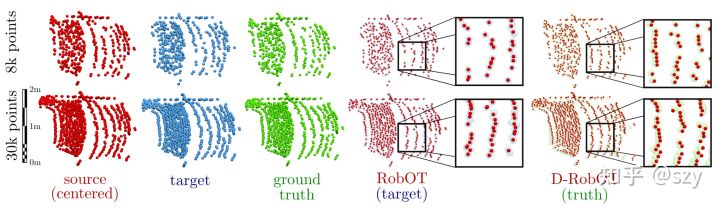
Fig.4.7. Comparison between RobOT and D-RobOT on Kitti Dataset.

这里我们放大了局部场景，原始的数据中，source 和 target 有一一对应关系，所以我们可以知道他们的ground-truth flow. 但这里的source 和 target进行了单独随机采样，所以他们并没有点对点对应关系，不过ground truth场和source 采样方式相同所以他们之间存在一一对应。这里一个很有趣的结果就是 RobOT这个optimization-based 方法会倾向于过拟合target set，但D-RobOT(spline) 这个deep-learning based 结合spline regularized 方法避免了过拟合的发生，很好的对应到了ground truth flow。

从结果而言我们发现仅仅是 RobOT这种优化方法就在速度，运算量和精确度上胜过了大部分深度学习方法， D-RobOT 也是远胜其他深度学习算法，从这一方面也证明了最优传输以及深度学习结合的价值所在。

以上便是点云配准与最优传输的一些方法结合的探讨，内容很多细节和实验结果就略过了，有兴趣的同学可以阅读我们最近的工作，同时欢迎讨论和指正。

文章可以参考这里：Accurate Point Cloud Registration with Robust Optimal Transport

代码可以参考这里： https://github.com/uncbiag/shapmagn