详解Python-Numpy库的函数diagonal()并附函数diagonal()与函数diag()的区别

Posted 2022-07-19 昊虹图像算法

函数diagonal()用于返回数组(也可称为矩阵)的对角线元素。

在Numpy库中函数diag()也可用于返回数组的对角线元素，那么二者有什么区别呢？

我们先看二者的原型：

函数diag()的原型如下：

diag(v[, k])

函数diag()的原型如下：

diagonal(a[, offset, axis1, axis2])

diag()的参数k和diagonal()的参数offset的作用相同，都用于控制取哪根对角线的元素值(这里请联联想线性代数中的主对角线和副对角线的概念)。
这样，diagonal()就比diag()多了两个参数axis1, axis2，其功能就比diag()要强大些。那么其功能强大在哪里呢？
强大在于diagonal()可通过axis1, axis2去处理三维以上矩阵求对角线元素的问题。
所以函数diagonal()与函数diag()的区别就在于函数diagonal()能处理三维以上矩阵的对角线元素返回问题，而函数diag()只能处理二维以下矩阵上的对角线元素返回问题。

我们都知道只有二维矩阵才存在对角线，所以我们需要用两根轴去确定一个二维矩阵。axis1, axis2就是这个意思。

那么具体是怎么确定的呢？
以三维的矩阵为例，说明这个问题。

现有形状为(2,3,4)的三维矩阵A，,如下：

import numpy as np

A = np.array([[[9,  5,  2,  7],
             [7,  5,  2,  9],
             [5,  2,  9, 7]],

            [[1, 0, 2, 4],
             [4, 2, 1, 0],
             [0, 4, 2, 1]]])

我们可在三维空间按照函数diagonal()对三条轴(axis)的定义画出它，如下图所示：

注意，这里三条轴的定义和我们通常认为的不一样，通常我们认为axis0代表列维度，axis1代表行维度，axis2代表第三维度。但在函数diagonal()看来，axis2代表列维度，axis1代表行维度，axis0代表第三维度。刚好和我们通常认为的相反。
另外，还要注意：上图中axis1的方向画反了，axis1的方向应该是向下才对。

显然，从上图可以看出，由轴axis2和axis1构成的二维平面包含两个二维矩阵。
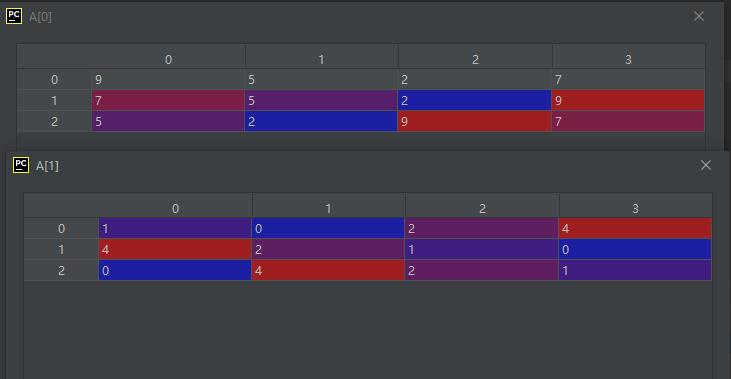
第一个二维矩阵就是A[0]，如下：

其主对角元素值为[9, 5 ,9]
第二个二维矩阵就是A[1]，如下：

其主对角元素值为[1, 2, 2]。
所以返回的对角元素矩阵应该是如下这个样子的：
$\left[\begin{array}{ccc}9& 5& 9\\ 1& 2& 2\end{array}\right]$
我们运行下代码，看下是不是这样：

import numpy as np

A = np.array([[[9,  5,  2,  7],
             [7,  5,  2,  9],
             [5,  2,  9, 7]],

            [[1, 0, 2, 4],
             [4, 2, 1, 0],
             [0, 4, 2, 1]]])

diag1 = np.diagonal(A, 0, axis1=1, axis2=2)

运行结果如下：

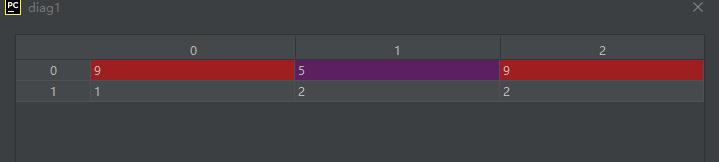
果然和我们分析的一样。

为了进一步验证博主的分析，再看由axis0和axis2组成的二维空间。

还是看这幅图，显然由axis0和axis2组成的二维空间由以下三个二维矩阵组成(注意：上图中axis1的方向画反了，axis1的方向应该是向下才对。)：
第1个：
$\left[\begin{array}{cccc}9& 5& 2& 7\\ 1& 0& 2& 4\end{array}\right]$
这个矩阵的主对角线元素为[9, 0]

第2个：
$\left[\begin{array}{cccc}7& 5& 2& 9\\ 4& 2& 1& 0\end{array}\right]$
这个矩阵的主对角线元素为[7, 2]

第3个：
$\left[\begin{array}{cccc}5& 2& 9& 7\\ 0& 4& 2& 1\end{array}\right]$
这个矩阵的主对角线元素为[5, 4]

有同学要问：为什么不是下面这个顺序？
第1个：
$\left[\begin{array}{cccc}5& 2& 9& 7\\ 0& 4& 2& 1\end{array}\right]$
这个矩阵的主对角线元素为[5, 4]

第2个：
$\left[\begin{array}{cccc}7& 5& 2& 9\\ 4& 2& 1& 0\end{array}\right]$
这个矩阵的主对角线元素为[7, 2]

第3个：
$\left[\begin{array}{cccc}9& 5& 2& 7\\ 1& 0& 2& 4\end{array}\right]$
这个矩阵的主对角线元素为[9, 0]

问得好，原因是实际上是把行维度索引(axis1)从0到2取值形成的三个二维矩阵，
当行维度为索引为0时，实际上是把所有的第0行取出形成一个二维矩阵；
当行维度为索引为1时，实际上是把所有的第1行取出形成一个二维矩阵；
当行维度为索引为2时，实际上是把所有的第2行取出形成一个二维矩阵；
所以这三个矩阵是有顺序的。

所以最终形成的对角线数组为：
$\left[\begin{array}{cc}9& 0\\ 7& 2\\ 5& 4\end{array}\right]$

我们看一下是不是我们上面分析的结果：

import numpy as np

A = np.array([[[9,  5,  2,  7],
             [7,  5,  2,  9],
             [5,  2,  9, 7]],

            [[1, 0, 2, 4],
             [4, 2, 1, 0],
             [0, 4, 2, 1]]])

diag1 = np.diagonal(A, 0, axis1=0, axis2=2)

运行结果如下：

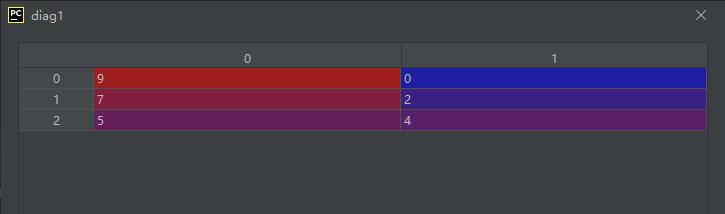
可见，果然和我们分析的一致。