基本算法-堆积树排序

Posted 2022-07-13 翟天保Steven

作者：翟天保Steven
版权声明：著作权归作者所有，商业转载请联系作者获得授权，非商业转载请注明出处

前言

       本文介绍一种排序算法——堆积树排序，是常用的排序算法之一。以下是本篇文章正文内容，包括算法简介、算法特点、算法实现和C++示例。

一、堆积树排序简介

       堆积树排序法是选择排序法的改进版，可以减少在选择排序法中的比较次数，进而减少排序时间。堆积排序法用到了二叉树的技巧，利用堆积树来完成排序。堆积树是一种特殊的二叉树，可分为最大堆积树和最小堆积树两种。

       最大堆积树满足3个条件：

1. 完全二叉树。
2. 所有节点的值都大于或等于它左右子节点的值。
3. 树根是堆积树中最大的。

       最小堆积树满足3个条件：

1. 完全二叉树。
2. 所有节点的值都小于或等于它左右子节点的值。
3. 树根是堆积树中最小的。

       堆积树排序法的实现思路：

1. 将数列转换为堆积树形式。
2. 将树根提取出来，剩下的数列继续转换为堆积树；这相当于选择排序法中把最大值或最小值提取出来。
3. 直到剩下的数列中数据为1，排序结束。

二、算法特点

       1）归并排序n个数据，一般需要处理log2n次，每次处理的时间复杂度为O(n)。因此，最坏最好和平均的时间复杂度都是O(nlog2n)。

       2）稳定，合并过程不改变原序列过程。

       3）空间复杂度是O(n)，需要用一个同样尺寸的额外空间做辅助。

三、代码实现

       代码实现逻辑：

1. 所有情况下，时间复杂度均为O(nlog2n)。
2. 堆积排序法不稳定，因为顺序变了。
3. 只需要一个额外的空间，空间复杂度为O(1)。

// 生成最大堆积树
void CreateMaxHeapTree(vector<int> &data, int i, int size)

	// j是当前节点的左子树节点，因为是完全二叉树
	int j = 2 * i + 1;

	// temp是当前节点的值
	int temp = data[i];

	// flag标识符用来判断当前节点是否大于左右子树，如果满足条件，可以提前终止循环
	bool flag = false;

	// 二叉树分析
	while (j < size && !flag)
	
		// j+1是右子树节点，这一步的目的是选出左右子树中最大值和根替换
		if ((j + 1) < size)
		
			if (data[j] < data[j + 1])
				j++;
		
		// 如果当前节点大于左右子树了，说明下面的分支都满足堆积树条件，可终止循环
		if (temp >= data[j])
		
			j -= 1;
			flag = true;
		
		// 当前节点被更大的子树值替换，继续深入二叉树，找当前节点的合适位置
		else
		
			data[(j - 1) / 2] = data[j];
			j = 2 * j + 1;
		
	
	// 当前节点放置在其合适位置
	data[j / 2] = temp;


// 堆积排序
void HeapSort(vector<int>& data)

	// 从次最低层开始往上，建立堆积树，初始堆积树的建立很重要，相当于对数据进行一个大致的排序
	int size = int(data.size());
	for (int i = size / 2; i >= 0; --i)
	
		CreateMaxHeapTree(data, i, size);
	

	// 扫描n-1次，每次将最值放置在后面，类似选择排序法，但是选择最值的过程是通过二叉树进行的，所以复杂度约为log2n
	for (int i = size - 1; i > 0; --i)
	
		int temp = data[i];
		data[i] = data[0];
		data[0] = temp;
		CreateMaxHeapTree(data, 0, i);
	

四、C++示例

#include <iostream>
#include <iomanip>
#include <vector>
#include <string>

using namespace std;

// 展示当前顺序
void Show(vector<int> data)

	size_t size = data.size();
	for (size_t i = 0; i < size; ++i)
		cout << setw(6) << data[i];
	cout << endl;


int Mcount = 1;
// 生成最大堆积树
void CreateMaxHeapTree(vector<int> &data, int i, int size)

	// j是当前节点的左子树节点，因为是完全二叉树
	int j = 2 * i + 1;
	// temp是当前节点的值
	int temp = data[i];
	// flag标识符用来判断当前节点是否大于左右子树，如果满足条件，可以提前终止循环
	bool flag = false;
	// 二叉树分析
	while (j < size && !flag)
	
		// j+1是右子树节点，这一步的目的是选出左右子树中最大值和根替换
		if ((j + 1) < size)
		
			if (data[j] < data[j + 1])
				j++;
		
		// 如果当前节点大于左右子树了，说明下面的分支都满足堆积树条件，可终止循环
		if (temp >= data[j])
		
			j -= 1;
			flag = true;
		
		// 当前节点被更大的子树值替换，继续深入二叉树，找当前节点的合适位置
		else
		
			data[(j - 1) / 2] = data[j];
			j = 2 * j + 1;
		
	
	// 当前节点放置在其合适位置
	data[j / 2] = temp;


// 堆积排序
void HeapSort(vector<int>& data)

	cout << "堆积排序：\\n原始数据：\\n";
	Show(data);

	// 从次最低层开始往上，建立堆积树，初始堆积树的建立很重要，相当于对数据进行一个大致的排序
	int size = int(data.size());
	for (int i = size / 2; i >= 0; --i)
	
		CreateMaxHeapTree(data, i, size);
	

	cout << "第"<< Mcount << "次最大堆积树：\\n";
	Show(data);
	Mcount++;

	// 扫描n-1次，每次将最值放置在后面，类似选择排序法，但是选择最值的过程是通过二叉树进行的，所以复杂度约为log2n
	for (int i = size - 1; i > 0; --i)
	
		int temp = data[i];
		data[i] = data[0];
		data[0] = temp;
		CreateMaxHeapTree(data, 0, i);

		cout << "第" << Mcount << "次最大堆积树：\\n";
		Show(data);
		Mcount++;
	

	cout << "排序后结果：\\n";
	Show(data);


// 主函数
int main()

	vector<int> data =  9,11,567,0,-2,4,2,12,18,6,9,5378,-102,8 ;

	// 堆积排序
	HeapSort(data);

	system("pause");
	return 0;

       效果图：

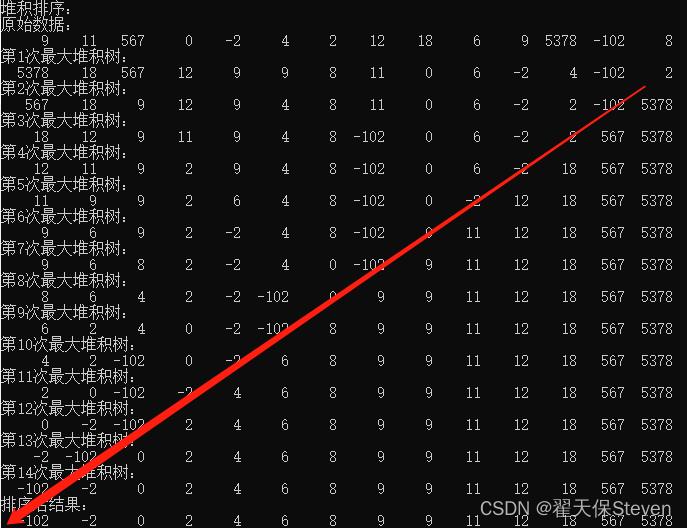
       综上所述，堆积排序法巧妙结合了堆积树，是不错的排序算法之一。但是，与其他排序算法相比，不太利于入门学习者理解，我尽可能以通俗的话语阐述，有表达不合理或者代码有问题的地方，烦请提出哦~

       如果文章帮助到你了，可以点个赞让我知道，我会很快乐~加油！