GPS仿真基于matlab GPS信号捕获跟踪定位仿真含Matlab源码 1960期
Posted 海神之光
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了GPS仿真基于matlab GPS信号捕获跟踪定位仿真含Matlab源码 1960期相关的知识,希望对你有一定的参考价值。
一、获取代码方式
获取代码方式1:
完整代码已上传我的资源:【GPS仿真】基于matlab GPS信号捕获跟踪定位仿真【含Matlab源码 1960期】
获取代码方式2:
通过订阅紫极神光博客付费专栏,凭支付凭证,私信博主,可获得此代码。
备注:
订阅紫极神光博客付费专栏,可免费获得1份代码(有效期为订阅日起,三天内有效);
二、GPS信号捕获跟踪定位简介
1 GPS信号结构
GPS卫星发送的信号主要由载波信号、扩频序列及导航数据三个方面构成, 其中载波信号是GPS信号传输的两个载波, 由于卫星与接收机处于相对关系, 接收机接收到到的信号会受到多普勒效应的影响, 根据多普勒频移能够确定接收设备三维运动速度, 以此来提高测距精度。扩频序列是伪随机码, 在此作用下, 数据能够拓展导航数据信号频谱, 以此来提高对信号的抗干扰性, 实现对物体的准确定位。
2 GPS卫星信号捕获算法分析
2.1 GPS卫星信号串行捕获
在本文设计中, 应用的捕获方式是CDMA系统中常见的捕获算法, 如图1。主要是建立在接收信号基础之上, 与本地产生伪码序列及本地载波之间的乘积。第一, 接收信号与本地产生伪码序列相乘, 形成之路信号, 然后与本地载波正交形成正交信号, 当两路信号相互交叉后, 能够完成跟踪目标。
对于伪码序列来说, 所有伪码的产生都进行了预先处理, 缺少即时性。首先利用C/A码产生器, 能够形成32个码, 然后将输入信号与所有可能经过码偏移C/A码相乘。
针对载波的形成, 作为捕获的第二步, 载波发生器需要产生相位差为90°两路载波信号, 即余弦与正弦两个信号。串行搜索最后一部分是余弦与正弦信号分别相乘, 并进行积分与平方处理后得出结论。如果本地与接收信号的伪码能够完全吻合, 那么获得的输出值较大。串行搜索捕获算法实现起来更为简单, 但是搜索范围过大, 且需要更多的时间, 无法实现对高动态目标的定位, 仅适用于低速、定位时间要求不高的接收机。而并行频率空间搜索算法, 只需要对C/A码移位即可, 能够在很大程度上缩短捕获时间。相比较来看, 两种算法都能够增加新的运算模块, 主要是在执行中需要重复多次利用原有模块, 且搜索范围较小, 捕获需要的时间更短。
2.2 分段FFT脉冲信号捕获算法
该算法核心思想, 是按照一定长度, 将若干毫秒输入信号进行分段处理, 捕获连续信号, 将各段结果以时间顺序进行排列, 最后得出具体的结果。在具体操作中, 可以从如下几个步骤进行:
(1) 将输入信号划分为10段, 采用点数补零至2n, 进行FFT运算。
(2) 对本地信号补零处理后进行FFT运算, 得出完整的结果。
(3) 将前两个数值进行相乘。
(4) 确定峰值位置后, 计算出两帧跳时数。
按照上述步骤能够找到三个明显的峰值, 可以将其作为码相位捕获结果。。另外, 观察仿真结果来看, 信噪比下降后, 信号只能够在分段1中检测到脉冲, 对应的峰均比为7.9475, 而处于第6、7段之间信号脉冲产生截断现象, 造成相关值有所下降, 并受到噪声干扰, 无法更加全面的呈现出来, 故无法监测到具体的数值, 且无法对其进行修复处理, 造成捕获失败。可见, 如果脉冲截断造成相关值损失, 该方法仅能够在低信噪比条件下极易出现捕获失败的情况, 无法对被测物体位置、速度等进行准确定位。
2.3 二次精频捕获算法
通过算法过程, 能够检测到信号有关峰值, 获得载波频率估计值。由于捕获算法频率分辨率与数据长度存在密切联系, 由1ms数据, 对应的频率分辨率约为1KHz, 对于后续跟踪环路而言过于粗糙。对此, 为了减少闭环时间, 我们需要对频率进行详细地估计。
根据FFT运算特点来看, 输入的数据填零后, 虽然无法提高分辨率, 且难以区分详细的频率信号, 但可以通过此找到单一信号。故直接采用较长数据后运用FFT计算并不恰当。为了减少FFT运算量, 可以利用相位关系算法, 完成二次精频捕获, 获取连续信号。将信号作为基础, 对其进行DFT运算, 求得最高频率分量。根据这一算法, 能够计算得出连续多个相位差值, 对所得相位差求平均值, 以此来提高频率准确性和可靠性。

图1:GPS卫星捕获算法
三、部分源代码
clc
clear
chiprate = 1.023e6; %码速率/码频率
IF = 9.548e6; %载波频率
samplingFreq = 38.192e6; %采样频率
codeLength = 1023; %码长
PRN = 18; %卫星号
%每个CA码周期的采样数,整数倍不好38192
samplesPerCode = round(samplingFreq /(chiprate/codeLength));
% 产生伪随机码,看cacode.m
w_code=cacode(PRN);
figure(1);
plot(w_code);
title('1023位gold码');
%对CA码进行采样
samplecacodes = makeCaTable(PRN,codeLength,chiprate,samplingFreq);
figure(2);
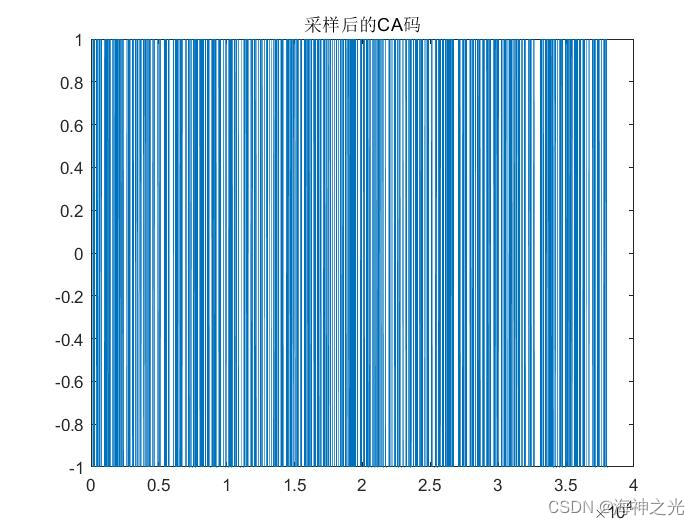
plot(samplecacodes);
title('采样后的CA码');
% 扩频,应该点乘离散的数据码
spread_code=samplecacodes;
figure(4);
plot(spread_code(1:5000));%这块注意只是取了5000个数据实际上有38192个
title('扩频后的数据')
%调制
t = (0:(samplesPerCode-1))/samplingFreq;
sendeddata=spread_code.*cos(2*pi*IF.*t);
figure(5);
plot(sendeddata(1:3000));
title('调制后的数据');
% 加噪声
data= awgn(sendeddata, -10); %加-20db分贝的白噪声
% figure(5);
% plot(data(1:38192));
% title('附加白噪声后的数据');
四、运行结果



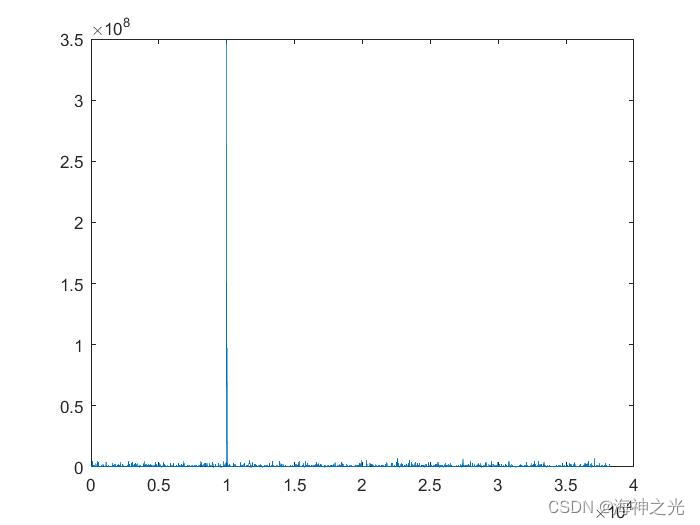
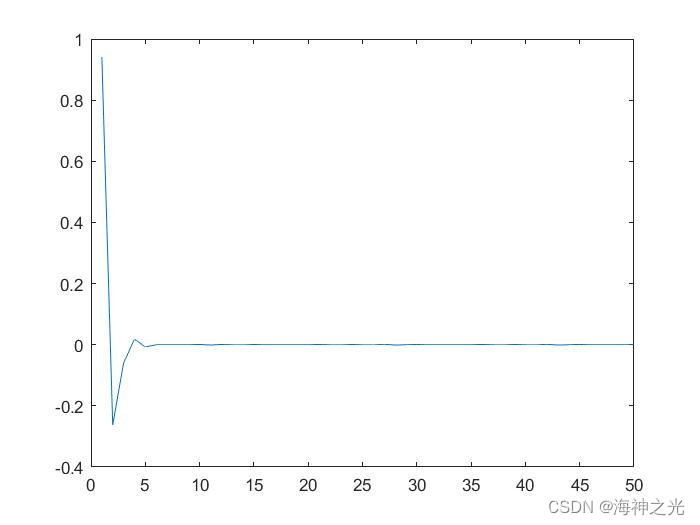
五、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1]刘紫薇.GPS卫星信号的捕获算法[J].电子技术与软件工程. 2017,(12)
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除
以上是关于GPS仿真基于matlab GPS信号捕获跟踪定位仿真含Matlab源码 1960期的主要内容,如果未能解决你的问题,请参考以下文章
GPS仿真基于matlab GPS信号捕获跟踪含Matlab源码 2126期
GPS信号跟踪捕获基于FPGA的GPS系统跟踪捕获算法的Verilog实现
VDLL矢量型GPS信号跟踪算法,矢量延迟锁定环的matlab仿真
滤波跟踪基于matlab不变扩展卡尔曼滤波器对装有惯性导航系统和全球定位系统IMU+GPS进行滤波跟踪含Matlab源码 2232期