因子分析怎么做?数据为啥要标准化?
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了因子分析怎么做?数据为啥要标准化?相关的知识,希望对你有一定的参考价值。
参考技术A
数据分析工作,并不是直接从分析开始的,当拿到一份要分析的数据,往往需要先进行一项基础工作-数据处理。数据处理一般的操作方法,正如SPSSAU【数据处理】板块中所提供的这些处理方法。
并且上图的【生成变量】方法中包涵了多种对数据变量重新处理的方法:
其中数据的标准化处理,是在进行很多数据分析之前都需要做的:
如果不进行标准化处理,后面的分析结果可能会存在误差。
数据的标准化处理主要是为了消除指标之间的量纲和取值范围差异的影响。什么是消除指标的量纲?一般情况下,我们所收集的数据是有单位的,比如收集到一份个人信息,其中包括人的身高和体重两个指标,身高有单位cm,体重有单位kg,消除指标的量纲就是消除它们的单位,当不同指标的量级差别很大时,消除量纲是有必要的,否则,数据的分析结果可能由量级较大的指标值决定,而忽略了量级小的指标,所以消除量纲,使之全部变成没有单位的数据,便于之后的分析。
例如下面的案例,需要对我国各省市的综合发展情况做因子分析,表中有六个指标。
像这样的数据,有的指标值特别大,有的指标值特别小,比如“高校数量”和“人均GDP”这两个指标,那么在进行因子分析之前,就需要先对这六个指标变量进行数据标准化。
数据标准化的处理中,使用最广泛的一种标准化方法是z-score标准化,这篇文章分享z-score标准化的原理和做法,以及怎么进行因子分析。
一、数据的Z-score标准化
(1)Z-score标准化原理
z-score标准化是基于原始数据的均值μ和标准差σ进行的,通过下面的转换公式,就可以将原始值转换为统一的均值为0,标准差为1的数据。
z-score标准化转换公式:
新得到的标准化数据的意义是“给定数据距离均值相对来说有多少个标准差”,在均值之上的数据会得到一个正的标准化分数,在均值之下的则得到一个负的标准化分数。标准化之后数据就会全部统一起来,不会有数据非常大比如10000,而有的数据非常小比如10。如下图:
适用: z-score标准化的方法适用于一个变量的最大值和最小值未知的情况,或有超出取值范围的离群数据的情况。
(2)使用SPSSAU对数据进行标准化处理
实际的分析操作中,数据标准化处理很简单,这里以上面的案例数据来演示如何做。
1、首先打开SPSSAU网站,上传好数据如下图:
2、对6个衡量各省市的综合发展情况的指标值进行标准化处理,在SPSSAU页面右侧选择【数据处理】版块中的【生成变量】按钮。
3、接着选择Z标准化方法,选中需要标准化的6个指标,点击【确认处理】即可。
4、处理结果
SPSSAU系统自动生成新的标准化后的指标变量,原始指标值仍然存在。
此时也可以查看具体的标准化后的数值,可以看到所有的数据都被压缩到了特定区间内:
这样就完成了数据标准化处理,接下来可以用标准化后的数据做因子分析了。
二、因子分析
SPSSAU中提供现成的因子分析方法,可以快速完成,操作如下:
(1)操作步骤
在SPSSAU页面左侧选择【进阶方法】中的【因子】按钮,将标准化后的6个指标变量拖拽到页面右侧的分析框中,根据研究实际情况选择因子数量,这里选择3个,点击【开始分析】即可得出因子分析结果。
(2)输出结果
SPSSAU共输出4个结果表格,自动生成2个可视化图形,分别如下:
1、KMO和Bartlett的检验:
因子分析探索定量数据可以浓缩为几个方面(因子),每个方面(因子)和题项对应关系;
第一:分析KMO值;如果此值高于0.8,则说明非常适合进行因子分析;如果此值介于0.7~0.8之间,则说明比较适合进行因子分析;如果此值介于0.6~0.7,则说明可以进行因子分析;如果此值小于0.6,说明不适合进行因子分析;
第二:如果Bartlett检验对应p值小于0.05也说明适合进行因子分析;
第三:如果仅两个分析项,则KMO无论如何均为0.5。
2、方差解释率表格
3、旋转后因子载荷系数表格
4、成份得分系数矩阵
5、碎石图
6、载荷图
7、线性组合系数及权重结果
三、总结
总之,在做因子分析之前,一般需要先进行数据标准化处理,消除数据指标的量纲影响,数据标准化与因子分析在SPSSAU在线SPSS数据分析工具中都被傻瓜化处理,只需要点点拽拽即可完成,更方便统计入门者使用。
因子分析
目录:
- 什么是因子分析
- 因子分析的作用
- 因子分析模型
- 因子分析的统计特征
- 因子载荷矩阵的估计方法
- 因子旋转
- 为什么要做因子旋转
- 因子旋转方法
- 因子得分
- 因子分析步骤
- 举例
- 因子分析和主成分分析区别
1、什么是因子分析?
因子分析是一种数据简化技术。
- 它通过研究众多变量间的依赖关系,探求观测数据中的基本数据结构,并且用少数几个假象变量(因子)来表示其基本数据结构;
- 这几个假想变量(因子)可以表示原来众多的原始变量的主要信息;
- 原始变量是可观测的显在变量,而假想变量是不可观测的潜在变量,即因子;
即一种用来在众多变量中辨别、分析和归结出变量间的相互关系并用简单的变量(因子)来描述这种关系的数据分析方法
如考察中学生的语文、英语、历史,数学、物理、化学成绩;
- 语文、英语、历史有很强的正相关;
- 数学、物理、化学有很强的正相关;
于是可以提取出两个因子:文科因子和理科因子
2、因子分析的主要作用?
- 寻求基本数据结构
- 数据简化
- 强相关问题会对分析带来困难
- 通过因子分析可以找出少数的几个因子替代原来的变量做回归分析、聚类分析和判别分析
3、因子分析模型

A称为因子载荷矩阵
4、统计特征
因子载荷$a_{ij}$是第i个变量与第j个公共因子的相关系数;
共同度:变量$X_i$的共同度是因子载荷矩阵的第i行的元素的平方和,记为$h_i^2=\\sum_{j=1}^{m}a_{ij}^2$;所有的公共因子和特殊因子对变量$X_i$的贡献为1,若$h_i^2$非常接近1,则因子分析的效果好,从原变量空间到公共因子空间的转化性质好;
贡献:因子载荷矩阵中各列元素的平方和$S_j=\\sum_{i=1}^p a_{ij}^2$,称为Fj对所有的$X_i$的方差贡献和,衡量Fj的相对重要性;
5、因子载荷矩阵的估计方法
- 主成分分析法
1)得到原始变量的相关系数矩阵;
2)主成分分析,得到特征值和特征向量;
3)确定因子个数(特征根大于1的;碎石原则:特征根从大到小排列,筛掉减小速度变缓的特征根);
4)载荷矩阵等于:特征向量*√(λ_i );
注:主成分分析法忽略了特殊因子。
- 主因子法
- 极大似然法
6、因子旋转(正交变换)

为什么要因子旋转?
- 因子分析的目的不仅仅是要找出公共因子以及对变量进行分组,更重要的是要知道每个公共因子的意义,以便进行进一步的分析。如果每个公共因子的含义不清,则不便于进行实际背景的解释。
- 初始因子的综合性太强,难以找出因子的实际意义。由于因子载荷阵是不唯一的,所以可以对因子载荷阵进行旋转,使因子载荷阵的结构简化,使其每列或行的元素平方值向0和1两极分化。
因子旋转方法
- 方差最大法:使得每个因子上的载荷尽量拉开差距,各自趋向于0,1;
- 四次方最大法:使得每个变量上的载荷尽量拉开差距,各自趋向于0,1;
- 等量最大法:结合上两个方法;
7、因子得分
当我们需要用因子再做分析时,就需要对因子进行测度,给出公共因子的值;

因子得分函数:把因子表示成原变量的线性组合;(得不到精确的值,只能估计)
方法:
- 巴特莱特因子得分(加权最小二乘法)
- 回归方法
8、因子分析步骤
1)选择分析的变量
因子分析的前提条件是观测变量间有较强的相关性,因为如果变量之间没有相关性或者相关性较小的话,他们不会有共享因子;
2)计算所选原始变量的相关系数矩阵
这也是判断所选变量是否有相关关系,如果没有,做因子分析是不恰当的;
3)提取公共因子
需要确定因子求解的方法和因子的数目。跟经验关系很大,一般方差小于1的因子贡献就很弱了,或者累计贡献率可以达到60%;
4)因子旋转
通过坐标变换使得原始变量和尽可能少的因子有密切关系,这样的因子实际意义更易解释;
5)计算因子得分
有了因子得分值,则可以在以后的分析(聚类分析、回归分析)中继续使用因子;
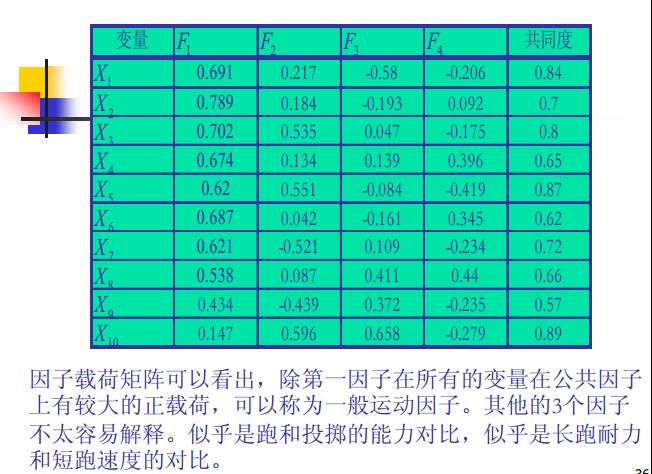
9、举例

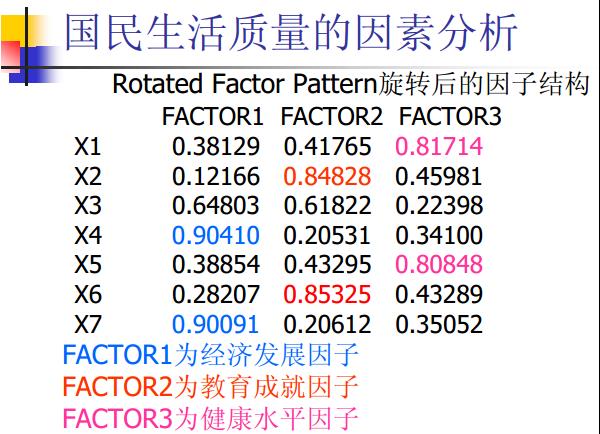

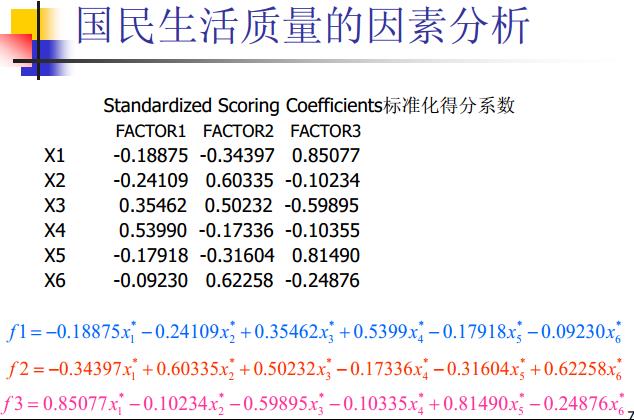
注:
因子分析是十分主观的,得到的因子究竟有什么意义也都是凭借自己的先验知识才可以知道的,所以评价因子分析的质量也很主观了。
10、主成分分析和因子分析的区别
- 主成分分析仅是变量变换,而因子分析需要构造因子模型;
主成分分析是用原始变量的线性组合来表示新的综合变量,即主成分;
而因子分析是用潜在的假想变量和随机影响变量的线性组合来表示原始变量;因子分析除了公共因子外还有特殊因子。
- 由于模型的特点,因子分析还多了”因子旋转“这一步,旋转后的公共因子一般没有主成分那么综合,公共因子往往可以找到实际意义,而主成分一般没有实际意义;
最后:
若数据本身就十分的独立,就很难用少数的变量取表示原始变量,降维可能失败,数据越相关,降维效果越好,可用如下办法进行变量间的相关性检验:
- KMO样本测度:KMO>0.7:适合;KMO<0.5:不适合;
- 巴特莱特球体检验:H0:相关系数矩阵R为单位阵,拒绝H0可作因子分析;
以上是关于因子分析怎么做?数据为啥要标准化?的主要内容,如果未能解决你的问题,请参考以下文章