ACM教程 - 快速排序（常规 + 尾递归 + 随机基准数）

Posted 2022-07-05 放羊的牧码

定义

快速排序是（Quick Sort）是对冒泡排序的一种改进，是非常重要且应用比较广泛的一种高效率排序算法。快速排序算法有两个核心点，分别为 哨兵划分 和 递归 。

• 哨兵划分

以数组某个元素（一般选取首元素）为 基准数 ，将所有小于基准数的元素移动至其左边，大于基准数的元素移动至其右边。

• 递归

对 左子数组 和 右子数组 分别递归执行 哨兵划分，直至子数组长度为 1 时终止递归，即可完成对整个数组的排序。

快速排序是通过多次比较和交换来实现排序，在一趟排序中把将要排序的数据分成两个独立的部分，对这两部分进行排序使得其中一部分所有数据比另一部分都要小，然后继续递归排序这两部分，最终实现所有数据有序。

• 步骤如下

1. 首先设置一个分界值也就是基准值又是也称为监视哨，通过该分界值将数据分割成两部分。
2. 将大于或等于分界值的数据集中到右边，小于分界值的数据集中到左边。一趟排序过后，左边部分中各个数据元素都小于分界值，而右边部分中各数据元素都大于或等于分界值，且右边部分个数据元素皆大于左边所有数据元素。
3. 然后，左边和右边的数据可以看成两组不同的部分，重复上述 1 和 2 步骤。当左右两部分都有序时，整个数据就完成了排序。

• 稳定性：根据 相等元素 在数组中的 相对顺序 是否被改变，排序算法可分为「稳定排序」和「非稳定排序」两类。
• 就地性：根据排序过程中 是否使用额外内存（辅助数组），排序算法可分为「原地排序」和「异地排序」两类。一般地，由于不使用外部内存，原地排序相比非原地排序的执行效率更高。
• 自适应性：根据算法 时间复杂度 是否 受待排序数组的元素分布影响 ，排序算法可分为「自适应排序」和「非自适应排序」两类。「自适应排序」的时间复杂度受元素分布影响，反之不受其影响。
• 比较类：比较类排序基于元素之间的 比较算子（小于、相等、大于）来决定元素的相对顺序；相对的，非比较排序则不基于比较算子实现。

图解

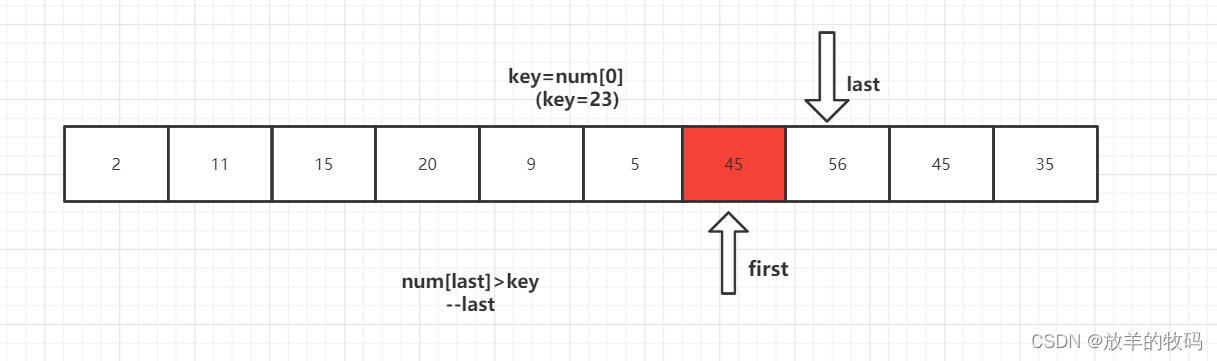
首先设置三个参数，first指向区间左端，last指向区间右端，key为当前的分界值。

从待排序的数据元素中选取一个通常为第一个作为基准值元素（key）key=num[0]，设置双指针first指向区间左端，last指向区间右端。

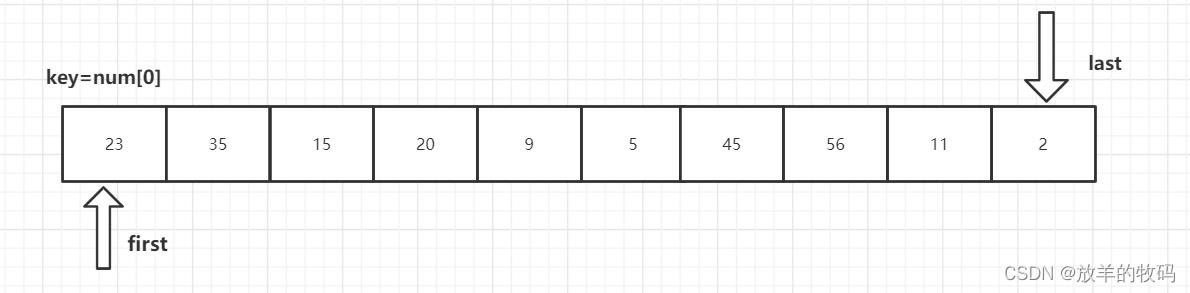
1、key 首先与 num[last] 进行比较，如果 num[last]<key，则num[first]=num[last]将这个比key小的数放到左边去，如果num[last]>=key则- -last，再拿num[last]与key进行比较，直到num[last]<key交换元素为止。

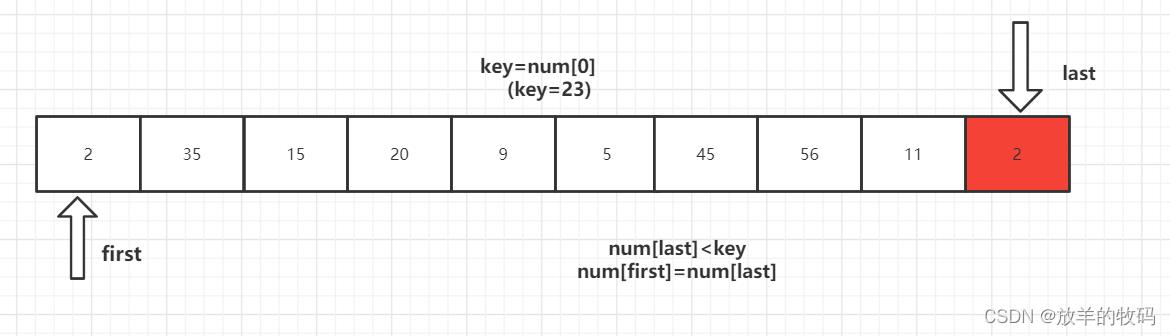
2、num[last]<key交换元素后，转向左边部分，用num[first]与key进行比较，如果num[first]<key,则++first，然后继续进行比较，直至num[first]>key,则将num[last]=num[first]。

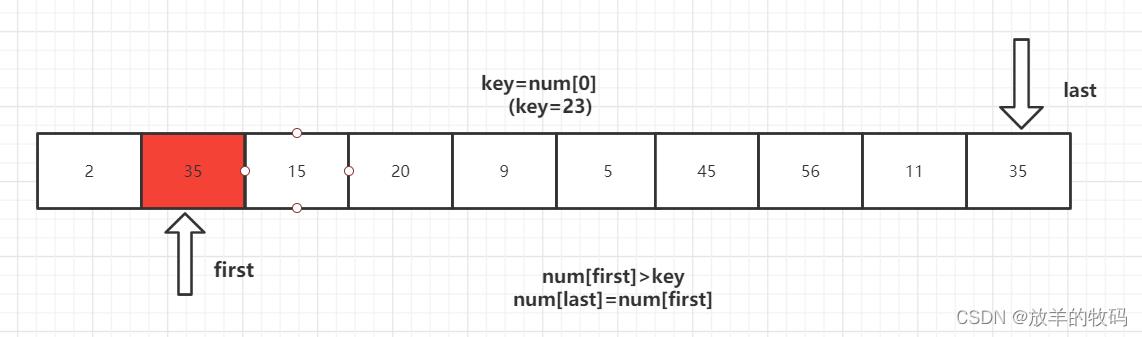
3、重复上述1、2步骤

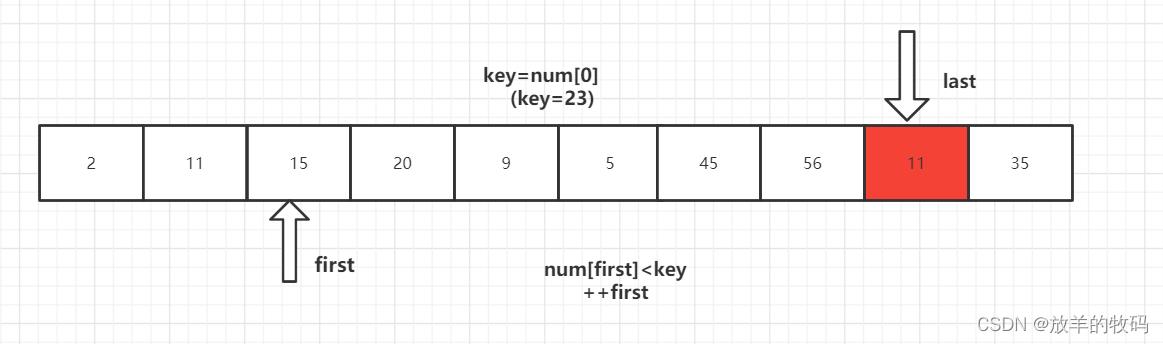
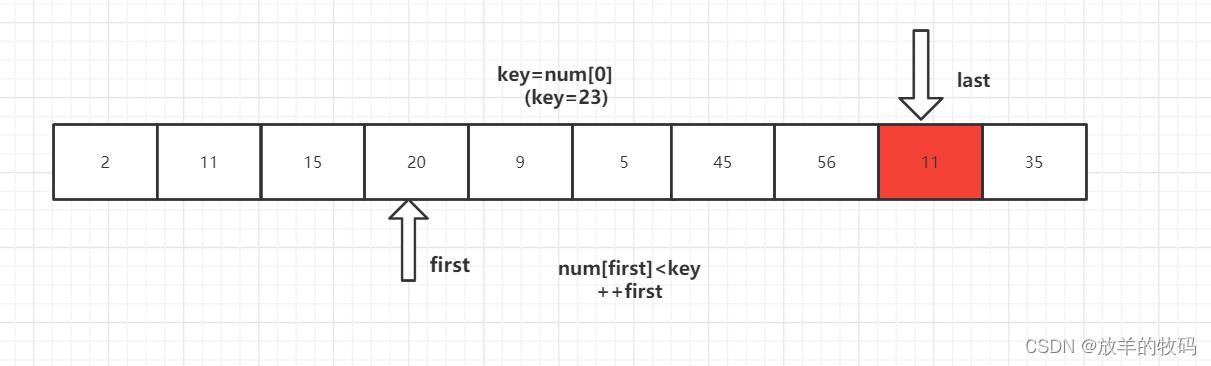
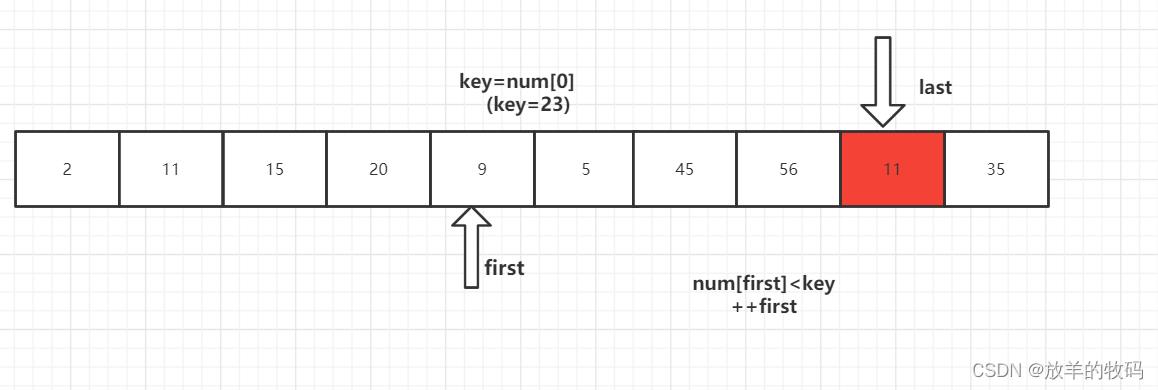
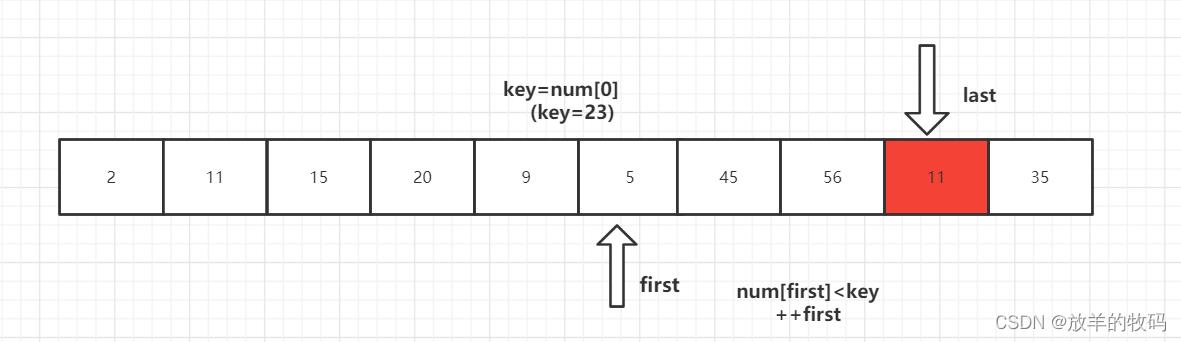
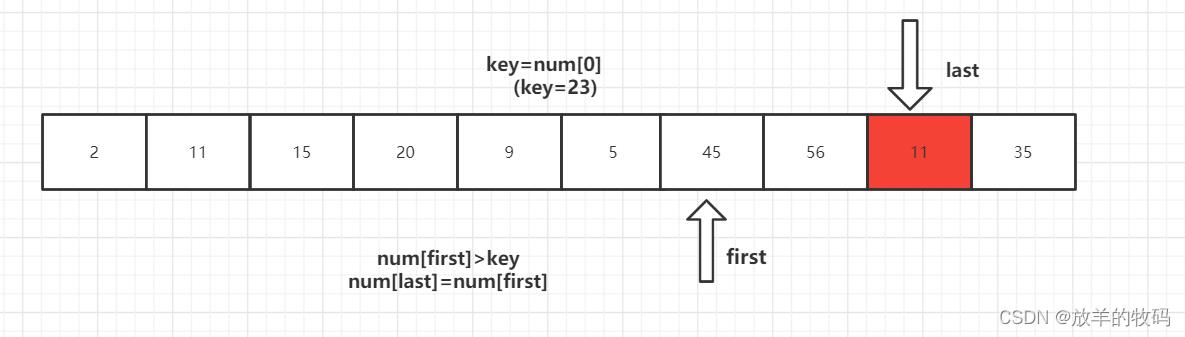
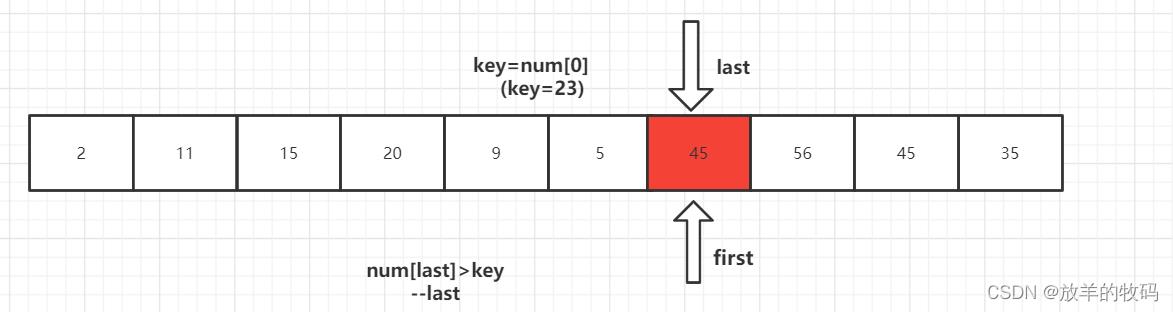
4、第一趟排序结束，得到 [2,11,15,20,9,5] 23 [56,45,35] 然后对左右子数列进行同样的操作。

2 [11,15,20,9,5] 23 [35,45] 56

2 [5,9] 11 [20,15] 23 35 45 56

2 5 9 11 15 20 23 35 45 56

完成从小到大的排序！！！

如下代码是预览版，啥意思呢？就是让你好理解，再到最后面的代码是最终优化版噢~

public static int[] quick_sort(int[] num, int l, int r)
    // r为数组元素总个数，last下标等于r-1
    int first=l,last=r-1,key=num[first];
    while(first<last)
        while(first<last&&num[last]>=key)
            --last;
        
        
        // 如果值小于 key分界值 交换
        num[first]=num[last];
        while(first<last&&num[first]<key)
            ++first;
        
        
        // 如果值大于key分界值 交换
        num[last]=num[first];
    
    num[first]=key;
    
    // 递归左右部分进行快排
    if (first>l) 
        num=quick_sort(num, l, first);
    
    if (first+1<r)
        num=quick_sort(num,first+1,r);
    
    
    return num;

性质

• 时间复杂度
  • 最佳 O(nlogn)

    • 最佳情况下， 每轮哨兵划分操作将数组划分为等长度的两个子数组；哨兵划分操作为线性时间复杂度 O(N) ；递归轮数共 O(logN) 。

  • 平均 O(nlogn)
    • 对于随机输入数组，哨兵划分操作的递归轮数也为 O(logN) 。
  • 最差 O()
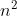    • 对于某些特殊输入数组，每轮哨兵划分操作都将长度为 N 的数组划分为长度为 1 和 N−1 的两个子数组，此时递归轮数达到 N 。
    • 通过 「随机选择基准数」优化，可尽可能避免出现最差情况，详情请见下文。
• 空间复杂度
  • 最差 O(n)
    • 快速排序的递归深度最好与平均皆为 logN ；输入数组完全倒序下，达到最差递归深度 N。
    • 通过「Tail Call（尾递归）」优化，可将最差空间复杂度降低至 O(logN) ，详情请见下文。
• 复杂度总结

  • 虽然平均时间复杂度与「归并排序」和「堆排序」一致，但在实际使用中快速排序 效率更高 ，这是因为：

    • 最差情况稀疏性： 虽然快速排序的最差时间复杂度为 O(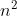) ，差于归并排序和堆排序，但统计意义上看，这种情况出现的机率很低。大部分情况下，快速排序以 O(NlogN) 复杂度运行。

    • 缓存使用效率高： 哨兵划分操作时，将整个子数组加载入缓存中，访问元素效率很高；堆排序需要跳跃式访问元素，因此不具有此特性。

    • 常数系数低： 在提及的三种算法中，快速排序的 比较、赋值、交换 三种操作的综合耗时最低（类似于插入排序快于冒泡排序的原理）。

• 稳定性：非稳定：哨兵划分操作可能改变相等元素的相对顺序。
• 就地性：原地：不用借助辅助数组的额外空间，递归仅使用 O(logN) 大小的栈帧空间。
• 自适应性：自适应：对于极少输入数据，每轮哨兵划分操作都将长度为 NN 的数组划分为长度 1 和 N−1 两个子数组，此时时间复杂度劣化至 O() 。
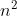• 比较类：比较 

常规版

• Java

void quickSort(int[] nums, int l, int r) 
    // 子数组长度为 1 时终止递归
    if (l >= r) return;
    // 哨兵划分操作
    int i = partition(nums, l, r);
    // 递归左（右）子数组执行哨兵划分
    quickSort(nums, l, i - 1);
    quickSort(nums, i + 1, r);


int partition(int[] nums, int l, int r) 
    // 以 nums[l] 作为基准数
    int i = l, j = r;
    while (i < j) 
        while (i < j && nums[j] >= nums[l]) j--;
        while (i < j && nums[i] <= nums[l]) i++;
        swap(nums, i, j);
    
    swap(nums, i, l);
    return i;


void swap(int[] nums, int i, int j) 
    // 交换 nums[i] 和 nums[j]
    int tmp = nums[i];
    nums[i] = nums[j];
    nums[j] = tmp;


// 调用
int[] nums =  4, 1, 3, 2, 5 ;
quickSort(nums, 0, nums.length - 1);

• C++

int partition(vector<int>& nums, int l, int r) 
    // 以 nums[l] 作为基准数
    int i = l, j = r;
    while (i < j) 
        while (i < j && nums[j] >= nums[l]) j--;
        while (i < j && nums[i] <= nums[l]) i++;
        swap(nums[i], nums[j]);
    
    swap(nums[i], nums[l]);
    return i;


void quickSort(vector<int>& nums, int l, int r) 
    // 子数组长度为 1 时终止递归
    if (l >= r) return;
    // 哨兵划分操作
    int i = partition(nums, l, r);
    // 递归左（右）子数组执行哨兵划分
    quickSort(nums, l, i - 1);
    quickSort(nums, i + 1, r);


// 调用
vector<int> nums =  4, 1, 3, 2, 5, 1 ;
quickSort(nums, 0, nums.size() - 1);

算法优化

快速排序的常见优化手段有「Tail Call」和「随机基准数」两种。

Tail Call（尾递归）

先来看下啥是尾递归好吧！

• 尾递归概念

如果一个函数中所有递归形式的调用都出现在函数的末尾，当递归调用是整个函数体中最后执行的语句且它的返回值不属于表达式的一部分时，这个递归调用就是尾递归。尾递归函数的特点是在回归过程中不用做任何操作，这个特性很重要，因为大多数现代的编译器会利用这种特点自动生成优化的代码。

• 尾递归原理

当编译器检测到一个函数调用是尾递归的时候，它就覆盖当前的活动记录而不是在栈中去创建一个新的。编译器可以做到这点，因为递归调用是当前活跃期内最后一条待执行的语句，于是当这个调用返回时栈帧中并没有其他事情可做，因此也就没有保存栈帧的必要了。通过覆盖当前的栈帧而不是在其之上重新添加一个，这样所使用的栈空间就大大缩减了，这使得实际的运行效率会变得更高。

快排的递归函数和尾递归有些类似，但因为调用了两次自身，所以并不属于尾递归，也不会被编译器优化。

但是，我们可以手动将第二个递归改为迭代，对其进行优化，节省栈空间。

Tips：两个调用函数位置可以颠倒，可以对任意一个进行优化，将其改为迭代。为了尽可能地节省递归栈，我们对比较两个区间的长度，对长度更长的进行优化，将其改为迭代。

由于普通快速排序每轮选取「子数组最左元素」作为「基准数」，因此在输入数组 完全倒序 时， partition() 的递归深度会达到 NN ，即 最差空间复杂度 为 O(N) 。

每轮递归时，仅对 较短的子数组 执行哨兵划分 partition() ，就可将最差的递归深度控制在 O(logN) （每轮递归的子数组长度都 ≤ 当前数组长度 / 2 ），即实现最差空间复杂度 O(logN) 。

代码仅需修改 quick_sort() 方法，其余方法不变，在此省略。

• Java

void quickSort(int[] nums, int l, int r) 
    // 子数组长度为 1 时终止递归
    while (l < r) 
        // 哨兵划分操作
        int i = partition(nums, l, r);
        // 仅递归至较短子数组，控制递归深度
        if (i - l < r - i) 
            quickSort(nums, l, i - 1);
            l = i + 1;
         else 
            quickSort(nums, i + 1, r);
            r = i - 1;
        
    

• C++

void quickSort(vector<int>& nums, int l, int r) 
    // 子数组长度为 1 时终止递归
    while (l < r) 
        // 哨兵划分操作
        int i = partition(nums, l, r);
        // 仅递归至较短子数组，控制递归深度
        if (i - l < r - i) 
            quickSort(nums, l, i - 1);
            l = i + 1;
         else 
            quickSort(nums, i + 1, r);
            r = i - 1;
        
    

优点

• 减少栈深度

对于划分不平衡的情况，传统版本栈深度最多可以达到O(n)，尾递归优化后，栈深度最多为O(lgn)。

例如：[1 2 3 4 5 6]最坏情况下 partion()函数 每次划分都选取末尾元素作为基准：6、5、4、3、2、1、0

未优化时

QSort(arr,0,6)——>QSort(arr,0,5)——>QSort(arr,0,4)——>QSort(arr,0,3)——>QSort(arr,0,2)——>QSort(arr,0,1)—>QSort(arr,0,0)

箭头表示新开辟的栈，栈深度达到了O(n)。

优化后该情况下只需要O(1)栈空间，因为左区间的递归被循环取代了。

Tips：网上的很多尾递归优化，固定优化右区间，对于上面的例子，仍然需要O(n)的栈深度。

• 栈深度减少了，因此大大增加了可排序的数据量，大大降低了爆栈的可能。

 

随机基准数

同样地，由于快速排序每轮选取「子数组最左元素」作为「基准数」，因此在输入数组 完全有序 或 完全倒序 时， partition() 每轮只划分一个元素，达到最差时间复杂度 O() 。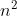

因此，可使用 随机函数 ，每轮在子数组中随机选择一个元素作为基准数，这样就可以极大概率避免以上劣化情况。值得注意的是，由于仍然可能出现最差情况，因此快速排序的最差时间复杂度仍为 O() 。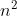

代码仅需修改 partition() 方法，其余方法不变，在此省略。

• Java

int partition(int[] nums, int l, int r) 
    // 在闭区间 [l, r] 随机选取任意索引，并与 nums[l] 交换
    int ra = (int)(l + Math.random() * (r - l + 1));
    swap(nums, l, ra);
    // 以 nums[l] 作为基准数
    int i = l, j = r;
    while (i < j) 
        while (i < j && nums[j] >= nums[l]) j--;
        while (i < j && nums[i] <= nums[l]) i++;
        swap(nums, i, j);
    
    swap(nums, i, l);
    return i;

• C++

int partition(vector<int>& nums, int l, int r) 
    // 在闭区间 [l, r] 随机选取任意索引，并与 nums[l] 交换
    int ra = l + rand() % (r - l + 1);
    swap(nums[l], nums[ra]);
    // 以 nums[l] 作为基准数
    int i = l, j = r;
    while (i < j) 
        while (i < j && nums[j] >= nums[l]) j--;
        while (i < j && nums[i] <= nums[l]) i++;
        swap(nums[i], nums[j]);
    
    swap(nums[i], nums[l]);
    return i;