TSP基于matlab GUI免疫算法结合蚁群算法求解旅行商问题含Matlab源码 1910期
Posted 海神之光
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了TSP基于matlab GUI免疫算法结合蚁群算法求解旅行商问题含Matlab源码 1910期相关的知识,希望对你有一定的参考价值。
一、免疫算法结合蚁群算法求解旅行商问题简介
1 引言
旅行商问题(Traveling Salesman Problem,TSP)是具有重要意义的组合优化难题,已被证明属于NPC问题。它可简述为:给定一个边赋权图G=(V,E),寻找G的Hamilton圈C,使得C的总权ω(C)最小。TSP问题描述简单却难以求解,因而一直作为衡量各种优化算法性能的标准。近年来,人们从仿生学的机理中受到启发,提出了许多用于求解TSP问题的新方法,如:禁忌搜索算法、遗传算法、摸拟退火算法、人工免疫算法和蚁群算法等。然而,面对TSP问题的复杂性,每种算法都表现出各自的优势和缺陷。
人工免疫算法(Artificial Immune Algorithm,AIA)是近几年才提出的一种随机优化方法,它模拟生物免疫系统,用亲和力来描述抗体与抗原之间的匹配程度,用排斥力来描述两个抗体之间的相似程度,依据抗体与抗原之间的亲和力以及抗体与抗体之间的排斥力来选择抗体。在用AIA求解优化问题时,一个抗体用一个字符串表示,满足约束条件的最优解即是抗原,候选解即是抗体。抗体与抗原之间的亲和力反映了候选解与最优解的接近程度,也即反映候选解对目标函数和约束条件的满足程度;抗体与抗体之间的排斥力反映了不同候选解之间的异同,也即反映了抗体的多样性。保持抗体的多样性可以防止算法陷入局部最优解。AIA具有快速随机的全局搜索能力,但对于系统中的反馈信息利用不足,当求解到一定范围时往往做大量无为的冗余迭代,求解效率低。
蚁群算法(Ant Colony Algorithm,ACA)是由意大利学者M.Dorigo,A.Colorni,V.Manizzo等在90年代初提出来的一类新的模拟进化算法,它通过信息素的积累和更新来寻求最优解。它的特点是模拟自然界中蚂蚁的群体行为。科学家们发现,蚂蚁有能力在没有任何提示下找到从巢穴到食物源的最短路径,并且能随环境的变化而变化,适应性地搜索新的路径,产生新的选择。经研究发现,其根本原因是蚂蚁在寻找食物源时,在其走过的路上释放一种特殊的分泌物–信息素,后来的蚂蚁选择该路径的概率与当时这条路径上该物质的强度成正比。当一定路径上通过的蚂蚁越来越多时,其留下的信息素轨迹也越来越多,后来的蚂蚁选择该路径的概率也越高,从而更增加了该路径的信息素强度。而强度大的信息素会吸引更多的蚂蚁,从而形成一种正反馈机制。通过这种正反馈机制,蚂蚁最终可以发现最短路径。特别是,当蚂蚁巢穴与食物源之间出现障碍物时,蚂蚁不仅可以绕过障碍物,而且通过蚁群信息素轨迹在不同路径上的变化,经过一定时间的正反馈,最终收敛到最短路径。ACA具有分布式并行全局搜索能力,但由于初期信息素匮乏,致使求解速度缓慢。
2 基于人工免疫算法和蚁群算法的混合算法
2.1 算法的设计思想
基于人工免疫算法和蚁群算法的混合算法,其基本思想是算法前过程采用AIA,充分利用AIA的快速性、随机性、全局收敛性,寻找较优的可行解,算法后过程采用ACA,利用前过程中AIA获得的较优可行解,产生初始信息素分布,然后充分利用ACA的并行性、正反馈性,提高求解效率。
2.2 算法中人工免疫算子的构造
人工免疫算子有字符换位算子、字符串移位算子、字符串逆转算子和优质字符串的保留等几种。对于TSP问题,AIA的人工免疫算子的构造如下:
2.2.1 字符换位算子,可分为单对字符换位算子和多对字符换位算子
单对字符换位操作是随机取两个正整数i,j(1<i,j≤n,i≠j),以一定的概率pc交换抗体A=(c1,c2,…,cn)中的一对字符ci,cj的位置;多对字符换位操作是预先确定一个正整数uc,在抗体A=(c1,c2,…,cn)中随机取r(1<r燮uc)对字符作字符串换位操作。
2.2.2 字符串移位算子,可分为单个字符串移位算子和多个字符串移位算子
单个字符串移位操作是随机取两个正整数i,j(1<i,j≤n,i≠j),在抗体A=(c1,c2,…,cn)中取一个字符子串A1=(ci,ci+1,…,cj-1,cj),以一定的概率ps依次往右移动A1中的各个字符,最右边的一个字符则移动到最左边的位置;多个字符串移位操作是预先确定一个正整数us,在抗体A=(c1,c2,…,cn)中随机取r(1<r燮us)个字符子串作字符串移位操作。
2.2.3 字符串逆转算子,可分为单个字符串逆转算子和多个字符串逆转算子
单个字符串逆转操作是随机取两个正整数i,j(1<i,j≤n,i≠j),在抗体A=(c1,c2,…,cn)中取一个字符子串A1=(ci,ci+1,…,cj-1,cj),以一定的概率pi使A1中的各个字符首尾倒置;多个字符串逆转操作是预先确定一个正整数ui,在抗体A=(c1,c2,…,cn)中随机取r(1<r燮ui)个字符子串作字符串逆转操作。
2.2.4 优质字符串的保留
如果若干个抗体与抗原之间的亲和力都很大,且这些抗体中包含了一个相同的字符子串,则称这个字符子串为优质字符串。如果抗体中存在优质字符串,则在抗体产生过程中以概率po使该优质字符串不受破坏,即把该优质字符串当成一个字符看待,称为优质字符串的保留。
2.3 算法基本步骤
根据该文算法的设计思想,其基本步骤可描述如下:
步骤1输入问题和确定抗体的编码表示。
输入问题的目标函数和约束条件,作为AIA的抗原。AIA的抗体采用自然数编码方式,一个字符串代表一个候选解。对于n个城市的TSP问题,设其城市编码分别为1,2,…,n,并且把商人出发城市编为第1号,其它城市可随意编号。把这n个城市的编号任意排列成一个长度为n的字符串都可以形成一个抗体,因此抗体空间包含n!个抗体。为了缩小抗体空间,提高搜索效率,将每个人工抗体(字符串)的第一个字符固定为出发城市的编号1。这样,每个抗体只有(n-1)个字符可任意排列,抗体空间就只包含(n-1)!个抗体。
步骤2产生初始抗体并进行预处理。
在一般情况下,可按上述抗体编码方式,在解空间中随机产生N个抗体作为初始抗体,构成初始抗体群,其中N为抗体群中抗体的数目。考虑到TSP问题的任何一条路径都是闭合路径,从任一城市出发,要到达的下一个城市选择为未到过的城市中距该城市最近的一个。为了提高搜索效率,先对每一个初始抗体进行预处理,然后才开始算法的迭代计算。设初始抗体A=(c1,c2,…,cn),其中c1=1(即c1代表商人出发城市的编号),对A进行预处理的步骤是:
(1)随机取正整数r(1燮r燮n)。若r=c1=1,则令A′=(c′1,c′2,…,c′n)=A,转(3);若r=ck≠1(1<k燮n),则转(2)。
(2)对初始抗体A中的各个字符依次循环左移位(k-1)次,每次移位时,使ci+1移到ci(i=1,2,…,i-1)的位置,且使ck移到c1的位置。设移位以后初始抗体A变为A′,则A′=(ck,ck+1,…,cn,c1,c2,…,ck-1)。令A′=(c′1,c′2,…,c′n),其中c′1=ck,余类推。
(3)随机取c′m=c′1,令C=邀c′2,c′3,…,c′n妖,若对C中任一个元素c′k,都有d(c′m,c′l)燮d(c′m,c′k),c′l∈C,则把c′l置于A′中c′m+1的位置,此时A′变为A″,令A″=(c″1,c″2,…,c″n)。然后从C中删除元素c′l,再取c″m=c″1,重复上述步骤,直到C中的元素全部被删除为止。设这一步完成以后初始抗体A变为B。
(4)对初始抗体B中的各个字符依次循环右移位若干次,直到抗体中第一个字符为1为止,移位方法与(2)中的类似,但方向相反。
步骤3计算亲和力和排斥力。
对于TSP问题,可定义抗体B与抗原G之间的亲和力App(B)=1/(TB-TG)。其中TB,TG分别为抗体B与抗原G对应的旅行路线的总长度,TG也是所求的最短路线的总长度。因在计算结束之前并不知道TG的大小,可用一适当大的正数T(T<TG)代替TG。又因计算App(B)需作除法运算,可定义App(B)=TM-TB。其中TM为较大的正数,且要求TM大于任意抗体对应的旅行路线的总长度,则可避免在计算App(B)时作除法运算。因此,构造抗体B与抗原G之间的亲和力App(B)=TM-TB并计算App(B)。抗体与抗原之间的亲和力反映抗体与抗原之间的匹配程度,App(B)越大,说明抗体B与抗原G之间的匹配越好。
对于TSP问题,可定义抗体B1与抗体B2之间的排斥力Re p(B1,B2)=|TB1-TB2|并计算Re p(B1,B2)。其中TB1,TB2分别为抗体B1与抗体B2对应的旅行路线的总长度。抗体与抗体之间的排斥力反映抗体与抗体之间的差距,Re p(B1,B2)越大,说明抗体B1与抗体B2之间的差距越大。计算抗体群中所有抗体与当前最佳抗体之间的排斥力。
步骤4产生新抗体并计算其亲和力和排斥力。
构造适当的人工免疫算子,通过人工免疫算子的作用概率pc,ps,pi,po和预先确定的正整数uc,us,ui产生新抗体;同时,计算各个新抗体的亲和力App(B)和新抗体间的排斥力Re p(B1,B2)。若新抗体中有与抗原相匹配的抗体,或已满足预定的停机条件则停机,从而获得较优的可行解。否则转步骤5。
步骤5抗体选择。
按照“优胜劣汰”的自然选择机制,在新产生的若干个抗体中,选择出N个与抗原匹配得较好的抗体构成新的抗体群,转步骤4。
步骤6初始化参数τC、τG、m、ρ、α、β、Q,根据步骤4获得的较优可行解,生成信息素初始分布,将m只蚂蚁置于n个结点。
这里,τC是一个根据具体求解规模给定的信息素常数,τG是AIA求解结果转换的信息素值,m是蚁群中蚂蚁的数量,ρ(0≤ρ<1)为信息素轨迹的残留系数,α(α叟0)为边(i,j)信息素轨迹强度τij的相对重要性,β(β叟0)为边(i,j)能见度ηij的相对重要性,ηij为边(i,j)长度dij的倒数,Q为蚂蚁循环一周所释放的总信息量。在初始时刻,根据下式设置信息素的初值:

步骤7计算每只蚂蚁的选择概率,根据选择概率移动每只蚂蚁到下一结点。
设蚂蚁k在t时刻的转移概率为pkij(t),可行顶点集为U,则按下式的概率转移规则决定t时刻蚂蚁k由位置i转移到位置j:
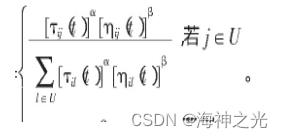
步骤8经过n个时刻,m只蚂蚁遍历个结点,完成一次循环。
设Δτkij为蚂蚁k在本次循环中在边(i,j)上留下的单位长度轨迹信息量,Zk为蚂蚁k在本次循环中所走路径的长度。此时,根据下式对各个路径信息素更新:

步骤9进行递归循环,直到满足算法的停止条件为止。
蚂蚁完成一个搜索周期,进入下一个循环。反复进行递归循环,直到周游计数器(总循环次数)NC达到预设值或所有蚂蚁都走同一周游路径便停止计算,输出近似最优解。
二、部分源代码
function varargout = ACO(varargin)
% ACO M-file for ACO.fig
% ACO, by itself, creates a new ACO or raises the existing
% singleton*.
%
% H = ACO returns the handle to a new ACO or the handle to
% the existing singleton*.
%
% ACO('CALLBACK',hObject,eventData,handles,...) calls the local
% function named CALLBACK in ACO.M with the given input arguments.
%
% ACO('Property','Value',...) creates a new ACO or raises the
% existing singleton*. Starting from the left, property value pairs are
% applied to the GUI before ACO_OpeningFcn gets called. An
% unrecognized property name or invalid value makes property application
% stop. All inputs are passed to ACO_OpeningFcn via varargin.
%
% *See GUI Options on GUIDE's Tools menu. Choose "GUI allows only one
% instance to run (singleton)".
%
% See also: GUIDE, GUIDATA, GUIHANDLES
% Edit the above text to modify the response to help ACO
% Last Modified by GUIDE v2.5 17-Apr-2022 16:39:44
% Begin initialization code - DO NOT EDIT
gui_Singleton = 1;
gui_State = struct('gui_Name', mfilename, ...
'gui_Singleton', gui_Singleton, ...
'gui_OpeningFcn', @ACO_OpeningFcn, ...
'gui_OutputFcn', @ACO_OutputFcn, ...
'gui_LayoutFcn', [] , ...
'gui_Callback', []);
if nargin && ischar(varargin1)
gui_State.gui_Callback = str2func(varargin1);
end
if nargout
[varargout1:nargout] = gui_mainfcn(gui_State, varargin:);
else
gui_mainfcn(gui_State, varargin:);
end
function ACO_OpeningFcn(hObject, eventdata, handles, varargin)
% This function has no output args, see OutputFcn.
% hObject handle to figure
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% varargin command line arguments to ACO (see VARARGIN)
% Choose default command line output for ACO
handles.output = hObject;
% Update handles structure
guidata(hObject, handles);
% --- Outputs from this function are returned to the command line.
function varargout = ACO_OutputFcn(hObject, eventdata, handles)
% varargout cell array for returning output args (see VARARGOUT);
% hObject handle to figure
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% Get default command line output from handles structure
varargout1 = handles.output;
%各TEXT和EDIT TEXT对象的回调函数,函数为空
function out_current_num_Callback(hObject, eventdata, handles)
% hObject handle to out_current_num (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% Hints: get(hObject,'String') returns contents of out_current_num as text
% str2double(get(hObject,'String')) returns contents of
% out_current_num as a double
function out_current_num_CreateFcn(hObject, eventdata, handles)
% hObject handle to out_current_num (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles empty - handles not created until after all CreateFcns called
% Hint: edit controls usually have a white background on Windows.
% See ISPC and COMPUTER.
if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))
set(hObject,'BackgroundColor','white');
end
function out_glob_num_Callback(hObject, eventdata, handles)
% hObject handle to out_glob_num (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% Hints: get(hObject,'String') returns contents of out_glob_num as text
% str2double(get(hObject,'String')) returns contents of out_glob_num
% as a double
function out_glob_num_CreateFcn(hObject, eventdata, handles)
% hObject handle to out_glob_num (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles empty - handles not created until after all CreateFcns called
% Hint: edit controls usually have a white background on Windows.
% See ISPC and COMPUTER.
if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))
set(hObject,'BackgroundColor','white');
end
function in_ant_num_Callback(hObject, eventdata, handles)
% hObject handle to in_ant_num (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% Hints: get(hObject,'String') returns contents of in_ant_num as text
% str2double(get(hObject,'String')) returns contents of in_ant_num as a double
function in_ant_num_CreateFcn(hObject, eventdata, handles)
% hObject handle to in_ant_num (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles empty - handles not created until after all CreateFcns called
% Hint: edit controls usually have a white background on Windows.
% See ISPC and COMPUTER.
if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))
set(hObject,'BackgroundColor','white');
end
三、运行结果
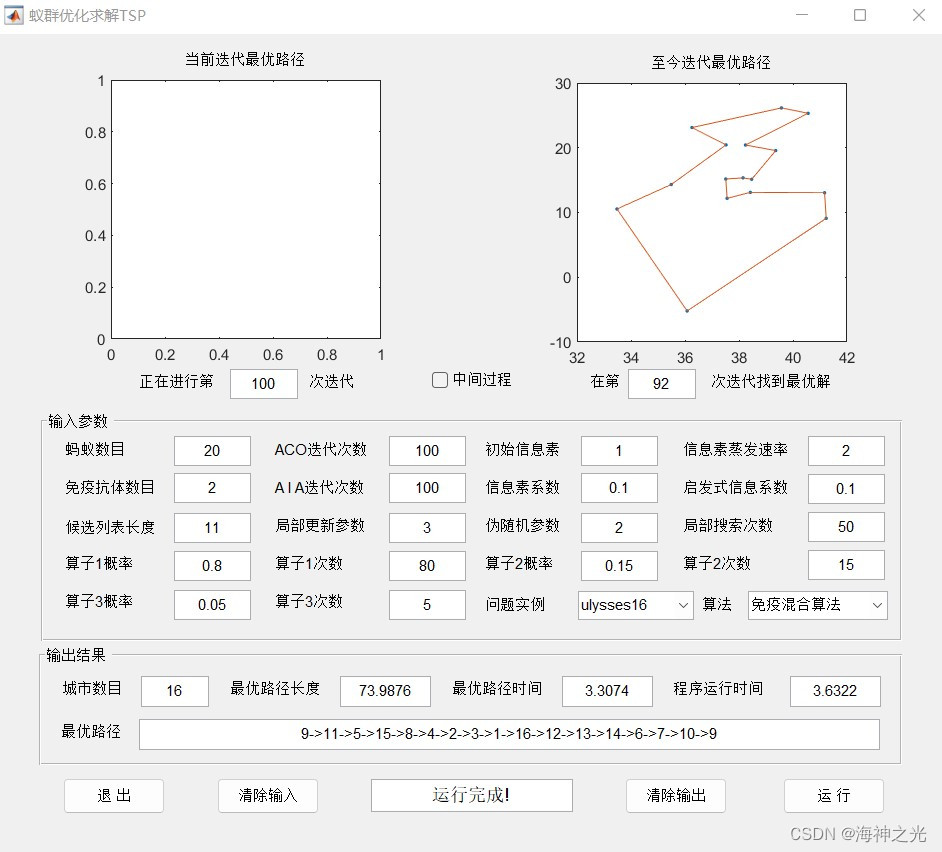
四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子工业出版社,2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社,2017.
[3]胡纯德,祝延军,高随祥.基于人工免疫算法和蚁群算法求解旅行商问题[J].计算机工程与应用. 2004,(34)
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除
以上是关于TSP基于matlab GUI免疫算法结合蚁群算法求解旅行商问题含Matlab源码 1910期的主要内容,如果未能解决你的问题,请参考以下文章