蒙特卡洛树搜索（MonteCarlo Tree Search）

Posted 2022-06-23 拉风小宇

问题描述

这个题目来自一个我的作业：
Construct a binary tree (each node has two child nodes) of depth $d=12$ and assign different values to each of the $2^d$ leaf-nodes. Implement the MCTS algorithm and apply it to the above tree to search for the optimal value.
我们看看能不能通过MCTS找到最大的叶子节点。

定义类和函数

我们需要定义类和函数，用来实现这个作业

节点类

在节点类中，有节点编号key，节点左右儿子left,right，父节点p，遍历次数n和回报和t。
此外还有两个方法判断其是否是叶子结点（没有子结点），以及计算该节点的UCB（Upper Confidence Bound）值，其实UCB在某种程度上就是在鼓励你多去走走还没走过的路，避免过早收敛

import math
# Python implementation to construct a Binary Tree from 
# parent array 
  
# A node structure 
class Node: 
    # A utility function to create a new node 
    def __init__(self, key, t, n): 
        self.key = key 
        self.left = None
        self.right = None
        self.t = t
        self.n = n
        self.p = None
    def get_parent(self, p):
        self.p = p
    def judge_leave_nodes(self):
        if (self.left == None) and (self.right == None):
            return True
        else:
            return False
    def calculate_UCB(self):
        C = 0.2
        if (self.n == 0):
            if self.judge_leave_nodes():
                UCB = self.t + 1000
            else:
                UCB = 1000
        else:
            UCB = self.t/self.n + C * math.sqrt(math.log(self.p.n)/self.n)
        return UCB

创建节点和树的函数

定义函数来创建树

def createNode(parent, T,N, i, created, root): 
  
    # If this node is already created 
    if created[i] is not None: 
        return
  
    # Create a new node and set created[i] 
    created[i] = Node(i,T[i],N[i]) 
    
    # If 'i' is root, change root pointer and return 
    if parent[i] == -1: 
        root[0] = created[i] # root[0] denotes root of the tree 
        return
  
    # If parent is not created, then create parent first 
    if created[parent[i]] is None: 
        createNode(parent, parent[i], T[i],N[i], created, root ) 
  
    # Find parent pointer 
    p = created[parent[i]]
    created[i].get_parent(p)
  
    # If this is first child of parent 
    if p.left is None: 
        p.left = created[i] 
    # If second child 
    else: 
        p.right = created[i] 
  
  
# Creates tree from parent[0..n-1] and returns root of the 
# created tree 
def createTree(parent): 
    n = len(parent) 
      
    # Create and array created[] to keep track  
    # of created nodes, initialize all entries as None 
    created = [None for i in range(n+1)] 
      
    root = [None] 
    for i in range(n): 
        createNode(parent, T, N, i, created, root) 
  
    return root[0] 

中序遍历树

用来中序遍历树，就是显示一下啦🙂

#Inorder traversal of tree 
def inorder(root): 
    if root is not None: 
        inorder(root.left) 
        print (root.key, root.t, root.n, root.p)
        inorder(root.right)  

MCTS函数

内含MCTS的四个步骤，即Selection、Expansion、Simulation和Backpropagation

def MCTS(root):
    node = root
    Rollout_node = None
    Previous_Rollout_node = root
    number_of_rollout = 0
    # choose the same path
    while (Rollout_node is not Previous_Rollout_node):
        # until reach leaf node
        while (node.judge_leave_nodes() is not True):
            left = node.left
            right = node.right
            ## Selection
            UCB_left = left.calculate_UCB()
            UCB_right = right.calculate_UCB()
            if (UCB_left >= UCB_right):
                node = left
            else:
                node = right
            # the node is the leaf node now, a rollout complete

        # backpropagation
        Previous_Rollout_node = Rollout_node
        Rollout_node = node
        number_of_rollout += 1
        #print ("Inorder Traversal of constructed tree")
        #print(inorder(root))

        while node.p is not None:
            node.p.t += Rollout_node.t
            node.p.n += 1
            node = node.p

    node = Rollout_node
    #print("The best path:")
    #while node.p is not None:
    #    print("%d<-" %(node.key), end='')
    #    node = node.p
    #print(root.key)
    #print("The Reward: %d" %(Rollout_node.t))
    print("The Number of Rollout: %d" %(number_of_rollout))
    return Rollout_node.t

我这里设置的结束条件是两次走同一条路，也就意味着别的路没有可能再试了，我感觉还是很makesense的。

测试效果

初始化一颗树

我们这里先做一颗简单的树，除了T的最后$2^{depth}$个数是我们制定的，其他的数都是和depth相关的，有规律的。

#           0:0 0
#          /      \\
#     1:0 0        2: 0 0
#    /    \\        /    \\
#3:2 0   4:1 0   5:-1 0  6:3 0      
parent = [-1, 0, 0, 1, 1, 2, 2]
T = [0, 0, 0, 2, 1, -1, 3]
N = [0,0,0,0,0,0,0]
root = createTree(parent)

print ("Inorder Traversal of constructed tree")
inorder(root)

MCTS(root)

通过3步，最终找到的是$0\to 1\to 3$这条路，得到的数是2

MCTS有问题？

我感觉MCTS的问题在上面的例子里还是看得出来，开始的时候都没有走过，会向左到1，然后向左到3，没毛病。第二次右边没走过到2，然后都没有走过向左到5。那么问题来了，2的值已经被5拉低了，也就是现在由于5的表现差拖累了2，进一步让6（原本是最好的）根本没有机会被遍历。这就是MCTS的问题。
不过这是因为5和6的数差的太多，实际上我感觉并不会，比如下围棋，我猜想你上一步走的很差，下一步大概率怎么走都不太行？（也说不准）
但是还是这个意思，MCTS的兄弟节点某种程度上在相互影响，甚至拖累。
不过既然没有所有都遍历，就得承担这个风险😏，你不能啥都要吧┓( ´∀` )┏

回归问题

现在我们设置$depth=12$也就是一共四千多个节点，先初始化数

import numpy as np
depth = 12

N = [0]*((2**(depth+1) -1))
T = [0]*((2**(depth) -1))
T.extend(np.random.randint(-100,101,2**(depth)).tolist())
import matplotlib.pyplot as plt
plt.hist(T[(2**(depth) -1):],bins = 100,color='red',histtype='stepfilled',alpha=0.75)
plt.title('distribution of T')
plt.show()

parent = [-1]
for i in range((2**depth) -1):
    parent.append(i)
    parent.append(i)

root = createTree(parent)
#print ("Inorder Traversal of constructed tree")
#inorder(root)
MCTS(root)

最后一层有四千多个数，我们从-100到100都有，所以理论上应该最优解是100.
我们做50次这个实验，看看得到的数都是多少（rewards）以及用多少步得到这个数（number_of_rollout）

import numpy as np
depth = 12
rewards = []
numbers_of_rollout = []

for i in range(50):
    N = [0]*((2**(depth+1) -1))
    T = [0]*((2**(depth) -1))
    T.extend(np.random.randint(-100,101,2**(depth)).tolist())
    import matplotlib.pyplot as plt

    parent = [-1]
    for i in range((2**depth) -1):
        parent.append(i)
        parent.append(i)

    root = createTree(parent)
    [R,N] = MCTS(root)
    rewards.append(R)
    numbers_of_rollout.append(N)

所有的子结点我们分配的数值为

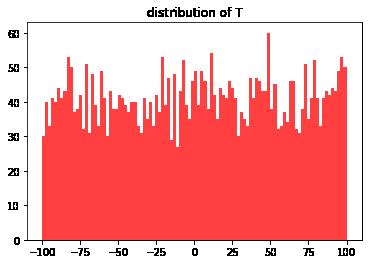
所以确实应该可以得到100，但是也有-100，平均值是-1.07。那我们看看MCTS的表现吧~

看看效果吧

我们画一下这两个的分布

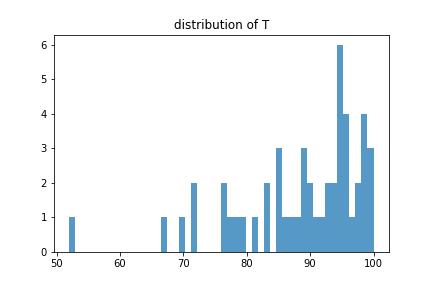
平均可以得到88.58，感觉还是可以的，除了那个五十几不太行，我猜他是被兄弟拖累了hhh？

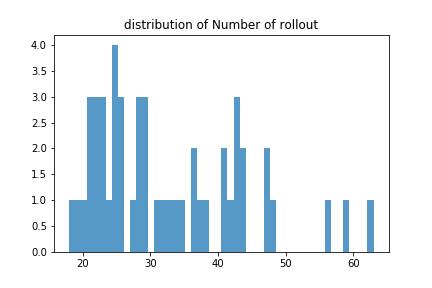
这个数我觉得更有用，平均32.56步就可以得到一个相对好的值，这太不容易了，把所有的遍历一遍要$2^{12}$步，省了也太多了吧，这么看起来88.58还是不错的✌️

C的作用

在UCB中C是用来平衡exploration和exploitation的。越大的C会让rollout的时候更加倾向于走那些没怎么走过的点，也就是走过的路应该会变得更多，得到的结果就应该会变得更好，让我们看一下实际效果吧~~

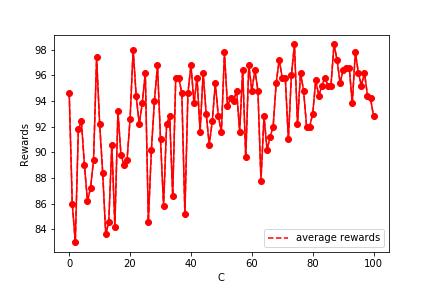
可以看出来确实是变好了一点，不太显著不过也可以理解，毕竟已经这么好了~~

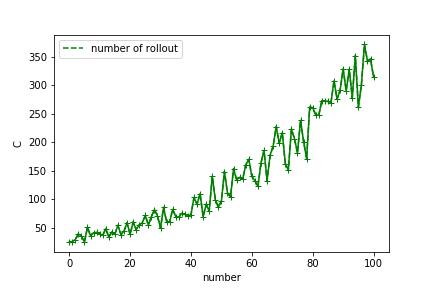
也可以看得出来明显rollout个数是在上升的~
C确实是在做一个平衡（tradeoff），到底是选择更好的reward还是更少的rollout，由你选择咯（practically choice）。
不过我看wiki说一般选择$\sqrt{(}2)$我也不知道为什么我这里的C仿佛应该取的很大的样子。。不管了问题不大
最后把最后一段的代码附上，还有个小tip，我发现np.log,np.sqrt比math.*好用哈哈哈

Rewards = []
Number_Of_Rolls = []

def frange(start, stop=None, step=None):

    if stop == None:
        stop = start + 0.0
        start = 0.0

    if step == None:
        step = 1.0

    while True:
        if step > 0 and start >= stop:
            break
        elif step < 0 and start <= stop:
            break
        yield ("%g" % start) # return float number
        start = start + step

import numpy as np
# Python implementation to construct a Binary Tree from 
# parent array
C = 0.0
while C <= 100:
# A node structure 
    class Node: 
        # A utility function to create a new node 
        def __init__(self, key, t, n): 
            self.key = key 
            self.left = None
            self.right = None
            self.t = t
            self.n = n
            self.p = None
        def get_parent(self, p):
            self.p = p
        def judge_leave_nodes(self):
            if (self.left == None) and (self.right == None):
                return True
            else:
                return False
        def calculate_UCB(self):
            #C = 0.2
            if (self.n == 0):
                if self.judge_leave_nodes():
                    UCB = self.t + 1000
                else:
                    UCB = 1000
            else:
                UCB = self.t/self.n + C * np.sqrt(np.log(self.p.n)/self.n)
            return UCB



    def createNode(parent, T,N, i, created, root): 

        # If this node is already created 
        if created[i] is not None: 
            return

        # Create a new node and set created[i] 
        created[i] = Node(i,T[i],N[i]) 

        # If 'i' is root, change root pointer and return 
        if parent[i] == -1: 
            root[0] = created[i] # root[0] denotes root of the tree 
            return

        # If parent is not created, then create parent first 
        if created[parent[i]] is None: 
            createNode(parent, parent[i], T[i],N[i], created, root ) 

        # Find parent pointer 
        p = created[parent[i]]
        created[i].get_parent(p)

        # If this is first child of parent 
        if p.left is None: 
            p.left = created[i] 
        # If second child 
        else: 
            p.right = created[i] 


    # Creates tree from parent[0..n-1] and returns root of the 
    # created tree 
    def createTree(parent): 
        n = len(parent) 

        # Create and array created[] to keep track  
        # of created nodes, initialize all entries as None 
        created = [None for i in range(n+1)] 

        root = [None] 
        for i in range(n): 
            createNode(parent, T, N, i, created, root) 

        return root[0] 

    #Inorder traversal of tree 
    def inorder(root): 
        if root is not None: 
            inorder(root.left) 
            print (root.key, root.t, root.n, root.p)
            inorder(root.right)
    def MCTS(root):
        node = root
        Rollout_node = None
        Previous_Rollout_node = root
        number_of_rollout = 0
        # choose the same path
        while (Rollout_node is not Previous_Rollout_node):
            # until reach leaf node
            while (node.judge_leave_nodes() is not True):
                left = node.left
                right = node.right
                ## Selection
                UCB_left = left.calculate_UCB()
                UCB_right = right.calculate_UCB()
                if (UCB_left >= UCB_right):
                    node = left
                else:
                    node = right
                # the node is the leaf node now, a rollout complete

            # backpropagation
            Previous_Rollout_node = Rollout_node
            Rollout_node = node
            number_of_rollout += 1
            #print ("Inorder Traversal of constructed tree")
            #print(inorder(root))

            while node.p is not None:
                node.p.t += Rollout_node.t
                node.p.n += 1
                node = node.p

        node = Rollout_node
        #print("The best path:")
        #while node.p is not None:
        #    print("%d<-" %(node.key), end='')
        #    node = node.p
        #print(root.key)
        #print("The Reward: %d" %(Rollout_node.t))
        #print("The Number of Rollout: %d" %(number_of_rollout))
        return (Rollout_node.t,number_of_rollout)


    import numpy as np
    depth = 12
    rewards = []
    numbers_of_rollout = []

    for i in range(5):
        N = [0]*((2**(depth小飞机之一——DQN与蒙特卡洛树搜索

 小飞机之一：DQN与蒙特卡洛树搜索
 蒙特卡罗(monteCarlo)
 分数在 0 和 n 之间时蒙特卡罗树搜索的 UCB 公式
 蒙特卡洛树搜索：井字游戏的实现
 Monte Carlo Tree Search – beginners guide