新版白话空间统计（12）：P值的表达以及空间统计上的特性

Posted 2022-06-21 虾神说D

CSDN的被爬虫专用声明：虾神原创，公众号\\知乎：虾神说D

转发、转载和爬虫，请主动保留此声明。

 

上篇文章简单介绍了P值与Z得分的一些基本概念，大家其实也都知道，P值和Z得分其实是有一定的相应关系的，Z得分有正负两种结果，而P值有显著和不显著两种可能。

如果按照我们一般的思维，P值和Z得分就应该有4种组合。不过实际上他们只有三种组合，如下：

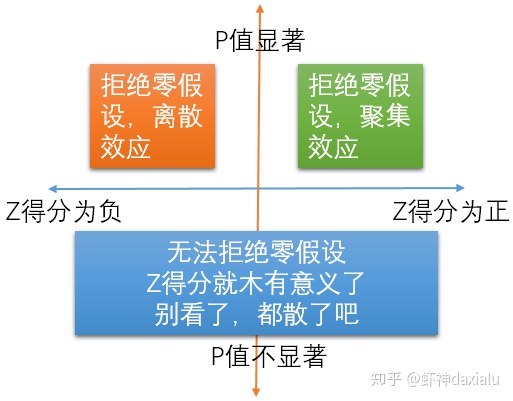
可以看见，只要P值不具备统计学上的显著特征，那么Z值不论是正负，都是一个结果。

Z值的计算很简单，标准差在任何软件或者数学工具包里面里面都内置了计算方法——就算没有内置，公式也挺简单的：

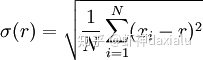
其中r是平均值。算出标准差来之后，用一个分数与平均数的差再除以标准差就可以了。但是P值的计算过程就比较神秘了——

所以这种剧本经常上演：

某大神答：很简单的拉，就是：

然后就是：

所以，到目前为止，还没有一个明确的公式这种说法，所有教程都是教大家用工具来计算的，比如Excel、R、Python、SPSS……

本着科普精神，今天我们有一个灰常简单的办法来讲讲P值计算的一些事情。

当然，直接通过Z得分，也是可以获取到P值的，因为P值和Z得分一般情况下是成双成对出现的，在正态分布区间中，两端的高Z得分，往往也是跟随者极小的P值。

但是，有的情况下，比如空间分布上面点模式分析随机性的一些计算（样方分析），就完全可以利用P值来进行标识了。

看看下面这个例子：

100个方格，100个点，如果均匀分布的话，应该是这个样子的：

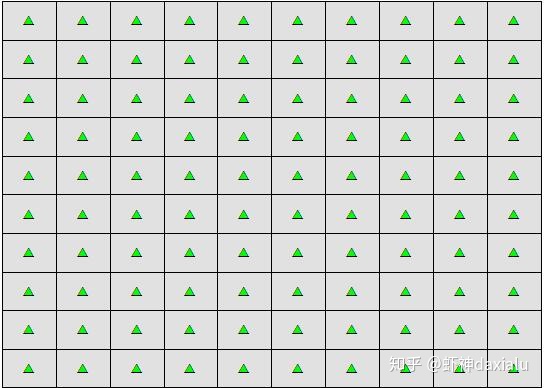
每个格子1个点，均匀分布（在空间统计学里面，有时候随机这个概念与均匀这个概念是通用的，比如下面这种分布：也是100个格子100个点，每个格子一个点……只不过在每个格网内这个点的位置是随机的。

如果说，1个格子正好1个点，那么就计数为1的话，100个格子，每个格子1个点，我们就正好计数为100……这个100如果转换为P值的描述方式，就是100%随机（均匀）。

接下去，我们移动其中一个格网内的点，把它放到另外一个格网里面去：

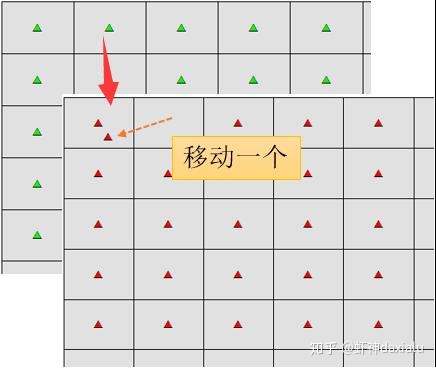
那么现在只有1个点的格网还剩下98个，另外有一个格网有2个点，有1个格网有0个点……这样，P值就变成了98，也就是98%的情况下是随机（均匀）的。

继续移动，我们会发现，随着点的往已知网格里面不断聚集，随机度会越来越小，最后如果极端情况是这样：

那么其中1个格网为100，另外99个都是0，这样，只有1个点的格网数，就是0了……这样就可以看出P = 0，完全无随机。

当然，根据费舍尔爵士的零假设原则，不需要p = 0,只需要p < 0.05就可以了，那么里面只需要有95个网格的点落进去的个数不等于1，就认为拒绝了零假设。

当然，这个例子是最简单的，当我们的格网数目和点的数据在不断变化的时候，我们的计算就不会这么简单了。所以说，在不同的校验下，P值的计算模式都是不一样的，根据工程学的方法来说，最容易进行的就是模拟计算，所以，业界对P值进行计算，大多数是通过蒙特卡洛模拟来实现的。

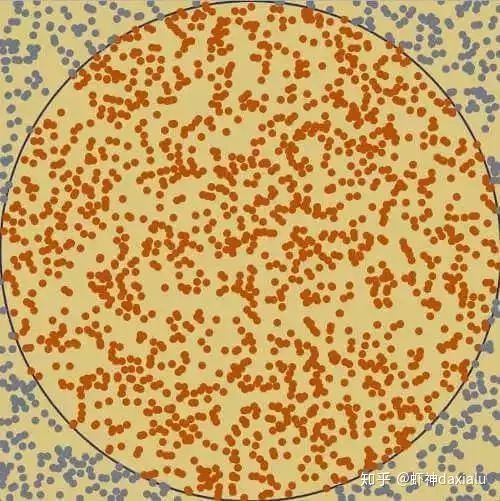
蒙特卡洛模拟最经典的应用案例，要计算一个圆（或者是其他不规则图形），只需要知道一个外接矩形的面积，然后在里面随机生成若干个点，有多少个点落在要计算的区域中，就认为这个区域占总区域的百分之多少，简单换算一下就可以了。

而我上面举的这个例子，很多时候也并不成立，比如下面这种情况：

一边50个格子，集中了100个点，每个格子2个……另外一边一个点也没有，都是0，那么这种情况，按照全局样本来看，是P值当然是0，拒绝零假设……但是我们如果仅仅看左半部分，50个格子100个点，每个格子均匀2个——p 值 = 100完全随机。

所以实际上，我上面举的例子，利用平均数来计算这种简单粗暴的方法，在很多时候都会出现各种问题。那么在实际应用和计算过程中，设定全局观察值和观察样本，以及对局部的数据进行观察计算，就非常有必要了。

这种特性，也就是空间异质性的一种表达……所以从下一节我们会讲讲空间异质性的一些事情：

继续回到P值。

随机的力量其实很强大的：

在自然条件下，随机是最完美的结果，随机表示了机会均等，表示无规律，无法预测，表示一切都是平滑的。在没有外在影响力的情况下，理论上一切都应该是随机的。

所以，我们通常把随机作为我们的零假设——假设不会出现任何影响，还原事件本来的样子——还原为上帝创造万物时候的本来样子。

那么随机在分析中，又能有什么样的表现呢？我们下回分解。

CSDN的被爬虫专用声明：虾神原创，公众号\\知乎：虾神说D

转发、转载和爬虫，请主动保留此声明。