论文阅读|深读node2vec: Scalable Feature Learning for Networks
Posted 海轰Pro
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了论文阅读|深读node2vec: Scalable Feature Learning for Networks相关的知识,希望对你有一定的参考价值。
目录
- 前言
- ABSTRACT
- 1. INTRODUCTION
- 2. RELATED WORK
- 3. FEATURE LEARNING FRAMEWORK 特征学习框架
- 4. EXPERIMENTS
- 5. DISCUSSION AND CONCLUSION
- 读后感
- 结语

前言
Hello!
非常感谢您阅读海轰的文章,倘若文中有错误的地方,欢迎您指出~
自我介绍 ଘ(੭ˊᵕˋ)੭
昵称:海轰
标签:程序猿|C++选手|学生
简介:因C语言结识编程,随后转入计算机专业,获得过国家奖学金,有幸在竞赛中拿过一些国奖、省奖…已保研。
学习经验:扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语!
唯有努力💪
本文仅记录自己感兴趣的内容
ABSTRACT
目前的特征学习方法还不足以表达网络中观察到的连接模式的多样性
node2vec
- 一个学习网络中节点连续特征表示的算法框架
- 最大限度地保留了节点的网络邻域
我们定义了一个灵活的节点网络邻域概念,并设计了一个有偏差的随机漫步过程,可以有效地探索不同的邻域。
我们认为,探索邻域的额外灵活性是学习更丰富的表征的关键
1. INTRODUCTION
目前的技术未能令人满意地定义和优化网络中可扩展的无监督特征学习所需的合理目标
node2vec
- 一种用于网络中可扩展特征学习的半监督算法
- 使用SGD优化了一个自定义的基于图的目标函数
- 返回的特征表示能最大限度地保留d维特征空间中节点的网络邻域
- 使用二阶随机游走方法为节点生成(采样)网络邻域。
我们的关键贡献在于灵活定义了节点网络邻居的概念
通过选择适当的邻域概念,node2vec可以学习基于其网络角色和/或其所属社区组织节点的表示。
我们通过开发一系列有偏差的随机漫步来实现这一点,这些漫步可以有效地探索给定节点的不同邻居。
所得到的算法是灵活的,通过可调参数让我们控制搜索空间,而不是之前工作中严格的搜索过程[24,28]。
我们还展示了如何将单个节点的特征表示扩展到节点对(即边)。
为了生成边的特征表示,只需使用简单的二元运算符组合学习到的单个节点的特征表示。这种组合性使得node2vec可以用于包括节点和边的预测任务。
我们的实验集中在网络中两个常见的预测任务:
- 一个是多标签分类任务,其中每个节点被分配一个或多个类标签;
- 另一个是链路预测任务,我们预测给定一对节点的边是否存在
实验表明
- node2vec在多标签分类和链路预测方面的性能分别达到26.7%和12.6%。
- 该算法对10%的标记数据具有较好的性能,并且对噪声或缺失边缘的扰动也具有鲁棒性。
- 在计算上,node2vec的主要阶段是可并行化的,它可以在几个小时内扩展到拥有数百万节点的大型网络。
2. RELATED WORK
无监督特征学习方法通常利用图的各种矩阵表示的光谱特性,特别是拉普拉斯矩阵和邻接矩阵
Unsupervised feature learning approaches typically exploit the spectral properties of various matrix representations of graphs, especially the Laplacian and the adjacency matrices
在线性代数的视角下,这些方法可以被视为降维技术
- 线性(如PCA)
- 非线性(如IsoMap)
缺点
- 矩阵分解开销很大
- 很难应用到大型网络
- 对于不同网络中的优化目标不具有鲁棒性(如同质性和结构等效性)
- 一般会对底层网络结构和预测任务之间的关系进行假设,造成不能在不同的网络上有效地泛化
受Skip-gram模型的启发,类似单词的有序序列一样,我们可以从底层网络中抽取节点序列,再利用Skip-gram模型进行训练
但是,节点可能的采样策略很多,导致学习到的特征表示不同
之前的工作的主要缺点:
- 没有一个明确的良好的采样策略可以适用于所有的网络、预测任务
- 不能提供从网络中采样节点的灵活性(采样策略不灵活)
引出node2vecv的优点:
- 通过设计一个不受特定采样策略约束的灵活目标,并提供参数来调整已探索的搜索空间(通过控制参数调整搜索空间)
对于基于节点和边缘的预测任务,最近有大量的工作是基于现有的和新的特定于图的深度网络架构进行监督特征学习[15,16,17,31,39]。
这些体系结构使用多层非线性变换直接最小化下游预测任务的损失函数,从而获得较高的精度
缺点:对训练时间具有高要求,以牺牲可伸缩性为代价。
3. FEATURE LEARNING FRAMEWORK 特征学习框架
我们将网络中的特征学习定义为一个极大似然优化问题
适用于任何有向(或无向)网络, 加权(或无权)网络
G = ( V , E ) G = (V, E) G=(V,E)
f : V → R d f : V \\rightarrow R^d f:V→Rd
将图 G G G的一个顶点 v v v映射为一个 d d d维向量,所有顶点对应的 d d d维向量构成一个大小为 ∣ v ∣ × d |v| \\times d ∣v∣×d的矩阵 ,也就是 f f f
N s ( u ) N_s(u) Ns(u):顶点u的邻域
其中 u ∈ V u\\in V u∈V, N s ( u ) ⊂ V N_s(u) \\subset V Ns(u)⊂V,注意这里的邻域是通过邻域采样策略 S S S生成的
通过采样策略 S S S,采集到的顶点u的邻域可能会不仅仅只局限其直接的邻居节点
运用Skip-gram架构的思路
对一个单词其最大概率的上下文
得到优化目标函数
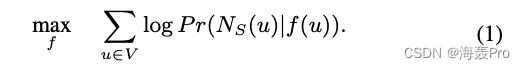
f ( u ) f(u) f(u)是顶点u的一个d维向量表示
P r ( N s ( u ) ∣ f ( u ) ) Pr(N_s(u)|f(u)) Pr(Ns(u)∣f(u))表示:顶点u的邻域对f(u)的概率
上面函数的意思大概就是:使得对所有顶点来说,其邻域对于其d维向量的概率之和最大
也就是说,对于每一个顶点,其邻域对于其d维向量的概率是存在的,我们的目标就是找出一个向量空间,使得每个顶点这样的概率之和最大
为了使优化问题易于处理,我们做了两个标准假设:
1)条件独立
假设观察一个邻域节点的可能性与观察任何其他邻域节点的可能性是独立的
简单的理解就是:顶点u的邻域对
f
(
u
)
f(u)
f(u)的概率可以想象为邻域中每一个顶点
n
i
n_i
ni对
f
(
u
)
f(u)
f(u)的概率的连乘
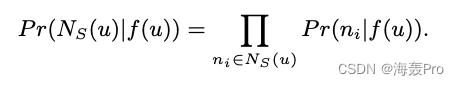
2)特征空间的对称性
源节点和邻域节点在特征空间中相互对称
因此我们将每个源邻节点对的条件似然建模为一个softmax单元,由其特征的点积进行参数化:
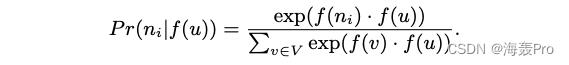
这里的意思大概就是:定义
P
r
(
n
i
|
f
(
u
)
)
Pr(n_i|f(u))
Pr(ni|f(u)),因为
P
r
(
n
i
|
f
(
u
)
)
Pr(n_i|f(u))
Pr(ni|f(u))这个概率是很模糊的,没有明确怎么求,作者这里就是通过向量空间中的不同顶点对应的向量之间的运算(就是上面式子)来明确表示
P
r
(
n
i
|
f
(
u
)
)
Pr(n_i|f(u))
Pr(ni|f(u))
通过以上两个假设的简化,等式1就可以写为
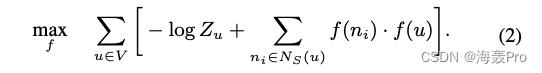
其中
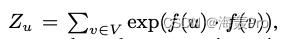
对于大型网络, Z ( u ) Z_(u) Z(u)的计算成本很高(),然后通过
负采样来近似等式2
使用随机梯度上升求等式2最优值
这里等式2是求max
一般求min时,是用SGD,也就是随机梯度下降
随机梯度下降/上升区别可以参考:https://blog.csdn.net/weixin_41245919/article/details/85091133
3.1 Classic search strategies 经典搜索策略
我们将源节点的邻域采样问题视为一种局部搜索的形式
为了能够公平地比较不同的采样策略 S S S
- 将邻域集 N S N_S NS的大小限制为 k k k个节点
- 对单个节点 u u u进行多个集合的采样(对每个节点进行多次采样)
一般情况下,产生k个节点的邻域集NS有两种极端采样策略:
- Breadth-first Sampling (BFS)
- Depth-first Sampling (DFS)
网络中节点的预测任务需要利用到节点的同质性和结构等价性两种相似性
- 同质性
- 结构等价
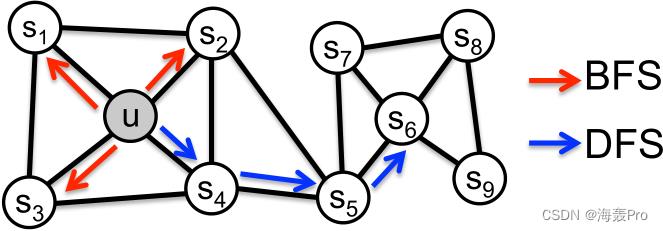
参考图1:
- 在同质性假设下,高度互连的节点,属于类似的网络集群或社区,应紧密嵌入在一起(如图1中的节点 s 1 s_1 s1和 u u u属于同一个网络社区)。
- 而在结构等价假设下,网络中具有相似结构角色的[10]节点应该紧密嵌入在一起(如图1中的节点 u u u和 s 6 s_6 s6作为其对应社区的枢纽)。
重要的是,与同质性不同,结构等价并不强调连通性:网络中的节点可以相隔很远,但仍然具有相同的结构作用
在现实世界网络中,这些等价概念并不是单独存在的
- 网络通常表现出这两种相似性,可能其中一些节点表现出同质性,而另一些则反映出结构等价
BFS 《==》结构等价:BFS采样的邻域导致了与结构等价性密切对应的嵌入
- 为了确定结构上的等价性,准确地描述局部邻域通常就足够了
- 此外,在BFS中,采样邻域中的节点往往会重复多次。这也很重要,因为它减少了表征1跳节点相对于源节点的分布的方差
- 然而,对于任何给定的 k k k(采样的节点数量),使用BFS,只有图的一小部分被探索到。
DFS 《==》同质性:DFS采样的节点更准确地反映了邻域的宏观情况
- 可以探索到网络的更大部分,因为它可以远离源节点u(样本大小k是固定的)
然而,DFS的问题在于
- 不仅要推断网络中存在哪些节点到节点的依赖关系
- 而且还要确定这些依赖关系的确切性质。这是很难的,因为我们有一个样本大小的限制和一个大的邻域来探索,导致高方差。
- 其次,移动到更大的深度会导致复杂的依赖关系,因为采样的节点可能离源很远,可能不太具有代表性
3.2 node2vec
基于上述观察结果,我们设计了一种灵活的邻域采样策略,使我们能够在BFS和DFS之间平滑地插值。我们通过开发一个灵活的有偏随机漫步程序来实现这一点,该程序可以以BFS和DFS的方式探索社区
3.2.1 Random Walks
形式上,给定源节点 u u u,我们模拟固定长度 l l l的随机游走。
令 c i c_i ci表示遍历中的第 i i i个节点,从 c 0 = u c_0 = u c0=u开始。
节点 c i c_i ci由以下分布生成:

式中
- π v x π_vx πvx为节点 v v v与 x x x之间的非标准化跃迁概率
- Z Z Z为标准化常数。
上式简单理解为:
- 节点v的下一个节点是节点x的概率为:如果节点v,x之间有边,则为 π v x Z \\fracπ_vxZ Zπvx,否则为0
3.2.2 Search bias α
最简单的有偏随机游走:
- 抽样下一个节点是基于静态边权值 w v x w_vx wvx,即 π v x π_vx πvx = w v x w_vx wvx。(对于非加权图, w v x w_vx wvx = 1)
然而,这并不允许我们考虑网络结构,并指导我们的搜索过程来探索不同类型的网络邻居。
这么简单的随机游走不行的
BFS和DFS是分别适用于结构等价和同质性的极端抽样范例
我们的随机游走应该适应这样一个事实
- 这些等价的概念不是竞争或排他性的,
- 现实世界的网络通常表现出两者的混合。
个人理解:
- BFS是适用于结构等价的采样策略
- DFS是适用于同质性的采样策略
- 两个方法都是极端的采样策略,只侧重一个方面的等价
- 真实的网络是存在两者等价关系的,我们需要通过参数控制,使得采样策略位于BFS和DFS之间
我们定义了一个二阶随机游走,通过两个参数 p p p和 q q q来引导游走
以下图为例
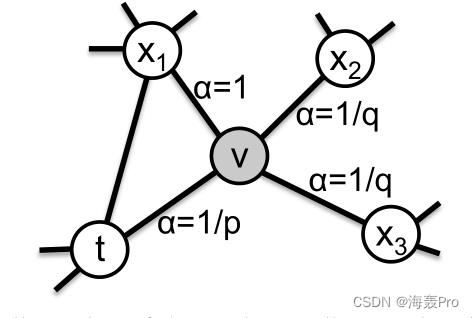
假设已经从节点 t t t遍历到节点 v v v(从 t t t游走到 v v v),现在位于节点 v v v
现在需要决定从v开始,下一步游走的节点是哪一个节点(也就是需要判断下一次游走)
因此需要计算从节点 v v v开始的边 ( v , x ) (v, x) (v,x)上的跃迁概率 π v x π_vx πvx
跃迁概率 π v x π_vx πvx:从节点 v v v游走到节点 x x x的概率
我们设非标准化跃迁概率为 π v x = α p q ( t , x ) ⋅ w v x π_vx = α_pq (t, x)·w_vx πvx=αpq(t,