图像处理中的线性代数知识及C/C++实现
Posted nanke_yh
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了图像处理中的线性代数知识及C/C++实现相关的知识，希望对你有一定的参考价值。
目录
在数字图像处理中我们是离不开线性代数的，了解线性代数基础知识又会有助于我们对图像处理算法的理解和实现。数字图像实质上就是二维的数字矩阵，对图像的操作，就是对这个矩阵的计算和操作。通过一系列的矩阵运算得到想要的变换结果，从而实现人体视觉上图像的变化。那么这篇文将主要讲一下图像处理中一般涉及到的线性代数基础知识和其代码实现。
对应线性代数，首先需要理解一些基础概念：标量、向量、张量和矩阵。这里面重点是矩阵及其相关的操作了。矩阵（matrix）：矩阵是一个二维数组，其中每一个元素由两个索引所确定，表示为A。
由 m × n 个数aij排成的m行n列的数表称为m行n列的矩阵，简称m × n矩阵。记作：
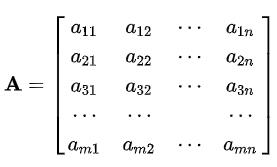
这m×n 个数称为矩阵A的元素，简称为元，数aij位于矩阵A的第i行第j列，称为矩阵A的(i,j)元，以数 aij为(i,j)元的矩阵可记为(aij)或(aij)m × n，m×n矩阵A也记作Amn。
这系列的定义均可在百度上看到：矩阵（数学术语）_百度百科 (baidu.com)。
在图像处理中，常用到的矩阵知识主要有：矩阵加法、减法和转置，再就是矩阵行列式、矩阵乘法和矩阵求逆。矩阵加减法对应元素进行逐个操作即可，这里不多说，着重讲矩阵转置、矩阵求行列式、矩阵乘法和矩阵求逆。
一、矩阵转置
转置（transpose）是矩阵的重要操作之一。矩阵的转置是以对角线为轴的镜像，这条从左上角到右下角的对角线被称为主对角线。一般将矩阵A的转置表示为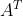
。
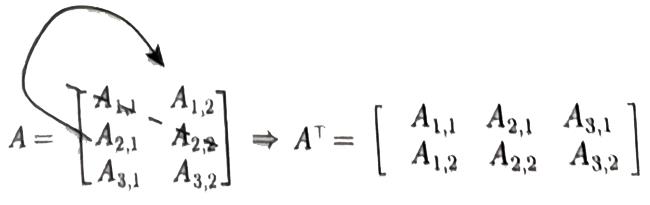
矩阵转置的实现：
/************************************************************************/
/* 功能：将一个矩阵的转置 */
/*参数：matrix 要转置的矩阵 */
/*参数：m 矩阵的行数 */
/*参数：n 矩阵的列数 */
/************************************************************************/
void transMatrix( double *matrix, int m, int n )
double *p; //临时存储作用
if( ( p = new double[m * n] ) == NULL || matrix == NULL)
return;
for( int i = 0; i < m; i++ )
for( int j = 0; j < n; j++ )
*( p + i * n + j ) = *( matrix + j * m + i ); //*p[i*n+j]=*matrix[j*m+i];
for( int i = 0; i < m; i++ )
for( int j = 0; j < n; j++ )
*( matrix + i * n + j ) = *( p + i * n + j );
delete []p;
二、矩阵行列式
一个n×n的正方矩阵A的行列式记为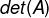
或者|A|,一个n×n矩阵的行列式等于其任意行（或列）的元素与对应的代数余子式乘积之和，即：
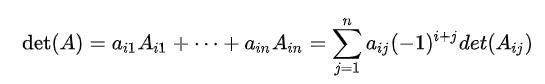
求行列式实现：
/************************************************************************/
/* 功能：将一个矩阵的行列式 */
/*参数：pt 要求行列式的矩阵 */
/*参数：rows 矩阵的行数 */
/*参数：cols 矩阵的列数 */
/*返回值：double 行列式的值 */
/************************************************************************/
double calMatrixdet(double *pt,int rows,int cols)
if(rows != cols)
cout<<"false"<<endl;
return -1;
else
if(rows == 2)//2x2矩阵
double result;
result = pt[0]*pt[3]-pt[1]*pt[2];
value = result;//返回行列式值
//cout<<"行列式的值："<<result<<endl;
else//非2x2矩阵
double num1 = 0;
double num2 = 0;
//求对角线的正值******************
double *sum1;
sum1 = new double [rows];
for(int s = 0;s < rows;s++)
sum1[s]=1;
for(int r = 0,c = 0;r < rows && c < cols;r++,c++)
if(s + c < rows)
sum1[s] *= pt[r*rows+s+c];
else
sum1[s] *= pt[(r-1)*rows+s+c];
for(int i = 0;i < rows;i++)
num1 += sum1[i];
//求对角线的负值*********************
double *sum2;
sum2 = new double [rows];
for(int w = 0;w < rows;w++)
sum2[w] = 1;
for(int r = 0,c = 2;r < rows && c >= 0;r++,c--)
if(w + c < rows)
sum2[w] *= pt[r*rows+w+c];
else
sum2[w] *= pt[(r-1)*rows+w+c];
for(int z = 0;z < rows;z++)
num2 += sum2[z];
//cout<<"正值："<<num1<<" "<<"负值："<<num2<<" "<<"行列式的值为："<<num1-num2<<endl;
delete[] sum2;sum2 = NULL;
delete[] sum1;sum1 = NULL;
double value = num1-num2;//返回行列式值
return value;
三、矩阵乘法
两个矩阵的乘法仅当第一个矩阵A的列数和另一个矩阵B的行数相等时才能定义。如A是m×n矩阵和B是n×p矩阵，它们的乘积C是一个m×p矩阵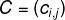
，它的一个元素：
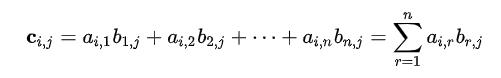
并将此乘积记为: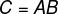
.
矩阵乘法实现：
/************************************************************************/
/* 功能：两个矩阵相乘 */
/*参数：FirMat 两个矩阵的第一个矩阵 */
/*参数：SecMat 两个矩阵的第二个矩阵 */
/*参数：OutMat 结果矩阵 */
/*参数：FirMatRow 第一个矩阵的行数 */
/*参数：FirMatColumn 第一个矩阵的列数 */
/*参数：SecMatColumn 第二个矩阵的列数 */
/************************************************************************/
int MatrixMult(double *FirMat, double *SecMat, double *OutMat, int FirMatRow, int FirMatColumn, int SecMatColumn)
int p, m, n;
for (p = 0; p < FirMatRow; p++)
for (n = 0; n < SecMatColumn; n++)
OutMat[p*SecMatColumn + n] = 0;
for (m = 0; m < FirMatColumn; m++)
OutMat[p*SecMatColumn + n] += FirMat[p*FirMatColumn + m] * SecMat[m*SecMatColumn + n];
return 0;
四、矩阵求逆
矩阵求逆，即求矩阵的逆矩阵。矩阵是线性代数的主要内容，很多实际问题用矩阵的思想去解既简单又快捷。逆矩阵又是矩阵理论的很重要的内容，逆矩阵的求法自然也就成为线性代数研究的主要内容之一。
设A是数域上的一个n阶方阵，若在相同数域上存在另一个n阶矩B，使得： AB=BA=E。 则我们称B是A的逆矩阵，而A则被称为可逆矩阵。其中，E为单位矩阵。矩阵A的矩阵逆记作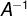
，其定义的矩阵满足以下条件：
典型的矩阵求逆方法有：利用定义求逆矩阵、初等变换法、伴随阵法、恒等变形法等。
矩阵求逆实现：
/************************************************************************/
/* 功能：求一个矩阵的逆（方阵） */
/*参数：matrix 要求逆的矩阵 */
/*参数：n 矩阵的阶数 */
/************************************************************************/
void inverseMatrix( double *matrix, int n )
int *is, *js, i, j, k, l, u, v;
double d, p;
is = new int[n * sizeof( int )];
js = new int[n * sizeof( int )];
for ( k = 0; k <= n - 1; k++ )
d = 0.0;
for ( i = k; i <= n - 1; i++ )
for ( j = k; j <= n - 1; j++ )
l = i * n + j;
p = fabs( matrix[l] );
if ( p > d )
d = p;
is[k] = i;
js[k] = j;
if ( d + 1.0 == 1.0 ) //判断该矩阵是否满秩
printf( "err**not inv矩阵求逆失败\\n" );
delete []is;
delete []js;
return;
if ( is[k] != k )
for ( j = 0; j <= n - 1; j++ )
u = k * n + j;
v = is[k] * n + j;
p = matrix[u];
matrix[u] = matrix[v];
matrix[v] = p;
if ( js[k] != k )
for ( i = 0; i <= n - 1; i++ )
u = i * n + k;
v = i * n + js[k];
p = matrix[u];
matrix[u] = matrix[v];
matrix[v] = p;
l = k * n + k;
matrix[l] = 1.0 / matrix[l];
for ( j = 0; j <= n - 1; j++ )
if ( j != k )
u = k * n + j;
matrix[u] = matrix[u] * matrix[l];
for ( i = 0; i <= n - 1; i++ )
if ( i != k )
for ( j = 0; j <= n - 1; j++ )
if ( j != k )
u = i * n + j;
matrix[u] = matrix[u] - matrix[i * n + k] * matrix[k * n + j];
for ( i = 0; i <= n - 1; i++ )
if ( i != k )
u = i * n + k;
matrix[u] = -matrix[u] * matrix[l];
for ( k = n - 1; k >= 0; k-- )
if ( js[k] != k )
for ( j = 0; j <= n - 1; j++ )
u = k * n + j;
v = js[k] * n + j;
p = matrix[u];
matrix[u] = matrix[v];
matrix[v] = p;
if ( is[k] != k )
for ( i = 0; i <= n - 1; i++ )
u = i * n + k;
v = i * n + is[k];
p = matrix[u];
matrix[u] = matrix[v];
matrix[v] = p;
delete []is;
delete []js;
五、解方程
最后，解方程组 Ax=b 中的未知数x该怎么实现呢？求解步骤如下：
/************************************************************************/
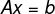
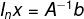
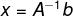
/* 功能：解方程组 Ax=b 中的未知数x */
/*参数：FirMatrix 第一个矩阵--------A */
/*参数：SecMatrix 第二个矩阵--------b */
/*参数：Row矩阵的行列数 */
/*参数：OutMatrix 要输出的矩阵 */
/************************************************************************/
bool SolveEquation_Gauss(double *FirMatrix, double *SecMatrix, int Row, double *OutMatrix)
int l, k, i, j, is, p, q, *js;
double d, t;
js = new int[Row];//方阵
l = 1;
//求行列式的值
for (k = 0; k <= Row - 2; k++)
d = 0.0;
for (i = k; i <= Row - 1; i++)
for (j = k; j <= Row - 1; j++)
t = fabs(FirMatrix[i*Row + j]);//求绝对值取正数
if (t > d)
d = t;
js[k] = j;
is = i;
if (d + 1.0 == 1.0)
l = 0;
else
if (js[k] != k)
for (i = 0; i <= Row - 1; i++)
p = i*Row + k;
q = i*Row + js[k];
t = FirMatrix[p];
FirMatrix[p] = FirMatrix[q];
FirMatrix[q] = t;
if (is != k)
for (j = k; j <= Row - 1; j++)
p = k*Row + j;
q = is*Row + j;
t = FirMatrix[p];
FirMatrix[p] = FirMatrix[q];
FirMatrix[q] = t;
t = SecMatrix[k];
SecMatrix[k] = SecMatrix[is];
SecMatrix[is] = t;
if (l == 0)
delete[]js;
return false;
d = FirMatrix[k*Row + k];
for (j = k + 1; j <= Row - 1; j++)
p = k*Row + j;
FirMatrix[p] = FirMatrix[p] / d;
SecMatrix[k] = SecMatrix[k] / d;
for (i = k + 1; i <= Row - 1; i++)
for (j = k + 1; j <= Row - 1; j++)
p = i*Row + j;
FirMatrix[p] = FirMatrix[p] - FirMatrix[i*Row + k] * FirMatrix[k*Row + j];
SecMatrix[i] = SecMatrix[i] - FirMatrix[i*Row + k] * SecMatrix[k];
d = FirMatrix[(Row - 1)*Row + Row - 1];
if (fabs(d) + 1.0 == 1.0)
delete[]js;
return false;
OutMatrix[Row - 1] = SecMatrix[Row - 1] / d;
for (i = Row - 2; i >= 0; i--)
t = 0.0;
for (j = i + 1; j <= Row - 1; j++)
t = t + FirMatrix[i*Row + j] * OutMatrix[j];
OutMatrix[i] = SecMatrix[i] - t;
js[Row - 1] = Row - 1;
for (k = Row - 1; k >= 0; k--)
if (js[k] != k)
t = OutMatrix[k];
OutMatrix[k] = OutMatrix[js[k]];
OutMatrix[js[k]] = t;
delete[]js;
return true;
当然直接利用以上的函数来求解也是可以的。具体的理解还是需要自己花费一定时间琢磨，如果只是使用的话，可以直接使用了，避免了自己再去研究和开发。
以上是关于图像处理中的线性代数知识及C/C++实现的主要内容，如果未能解决你的问题，请参考以下文章