机器学习笔记：并行计算 （基础介绍）

Posted 2022-06-01 UQI-LIUWJ

本篇用并行梯度下降作为引子，使用MapReduce框架，简单介绍一下并行计算。

1 并行梯度下降

1.1 最小二乘回归

我们记训练数据为

最小二乘回归定义为：

最小二乘回归的目标是寻找向量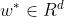，使得对于所有的j，都接近于yj。

同样地，我们可以用梯度下降解这个问题

 

 1.2 并行梯度下降

由于 x j 和 w 都是 d 维向量，因此计算一个 g ( x j , y j ; w ) 的时间复杂度是 O ( d ) 。【d次乘法】 计算梯度需要计算g函数n次——>的时间复杂度是O(nd)。 如果我们可以用m块处理器并行计算，那么理想情况下每块处理器的计算量是O(nd/m) 比如，我们有两块处理器，我们把 展开，有：

 

 两块处理器各承担一半的计算量，分别输出d维向量和

把两块处理器的结果汇总，有：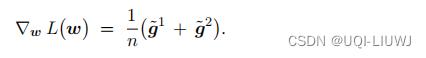

 

 1.3 并行梯度下降 的难点

并行梯度下降中的“计算”非常简单；而并行梯度下降的复杂之处在于 通信 。 在一轮梯度下降开始之前，需要把最新的模型参数 w 发送给两块处理器，否则处理器无法计算梯度。 在两块处理器完成计算之后，需要做通信，把结果 和汇总到一块处理器上。

2 MapReduce

• 并行计算需要在计算机集群上完成。
  • 一个集群有很多处理器和内存条，它们被划分到多个节点 (Compute Node) 上。
  • 一个节点上可以有多个处理器，处理器可以共享内存。
  • 节点之间不能共享内存，即一个节点不能访问另一个节点的内存。
  • 如果两个节点相连接， 它们可以通过计算机网络通信（比如 TCP/IP 协议）。

• 为了协调节点的计算和通信，需要有相应的软件系统。
  • MapReduce 是由 Google 开发的一种软件系统，用于大规模的数据分析和机器学习
  • MapReduce 原本是软件系统的名 字，但是后来人们把类似的系统架构都称作 MapReduce。
  • 除了 Google 自己的 MapReduce， 比较有名的系统还有 Hadoop 和 Spark
  • MapReduce 属于 Server-Client 架构，有一个节点作为中央服务器，其余节点作为 Worker，受服务器控制。
  • 服务器用于协调整个系统，而计算主要由 Worker 节点并行完成。

• 服务器可以与 Worker 节点做通信传输数据（但是 Worker 节点之间不能相互通信）。
  • 一种通信方式是广播 (Broadcast)，即服务器将同一条信息同时发送给所有 Worker 节点；
  • 如图 13.1 所示。比如做并行梯度下降的时候，服务器需要把更新过的参数广播 到所有 Worker 节点。
  • MapReduce 架构不允许服务器将一条信息只发送给一号节点，而将一条不同的信息只发送给二号节点。服务器只能把相同信息广播到所有节点。

•  每个节点都可以做计算。
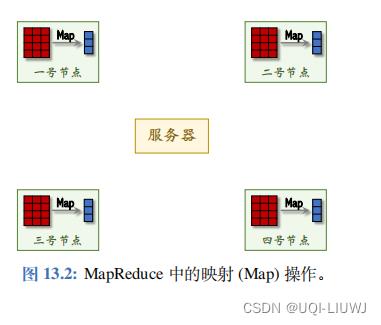
  • 映射 (Map) 操作让所有 Worker 节点同时并行做计算；
  • 如图 13.2 所示。如果我们要编程实现一个算法，需要自己定义一个函数，它可以让每个 Worker 节点把它的本地数据映射到一些输出值。
  • 比如做并行梯度下降的时候，定义函数 g 把三元组 映射到向量
  • 映射操作要求所有节点都要同时执行同一个函数 ，比如 g。 节点不能各自执行 不同的函数。

• Worker 节点可以向服务器发送信息，最常用的通信操作是规约 (Reduce)。
  • 这种操作可以把 Worker 节点上的数据做归并，并且传输到服务器上。
  • 如图 13.3 所示，系统对 Worker 节点输出的蓝色向量做规约。
    • 如果执行 sum 规约函数，那么结果是四个蓝色向量的加和。
    • 如果执行 mean 规约函数，那么结果是四个蓝色向量的均值。
    • 如果 执行 count 规约函数，那么结果是整数 4，即蓝色向量的数量。

3 数据并发与模型并发

数据并发 (Data Parallelism) ：为了使用 MapReduce 实现并行梯度下降，我们需要把 数据集 ( x 1 , y 1 ) , · · · , ( x n , y n ) 划分到 m 个 Worker 节点上，每个节点上存一部分数据，这种划分方式叫做数据并发。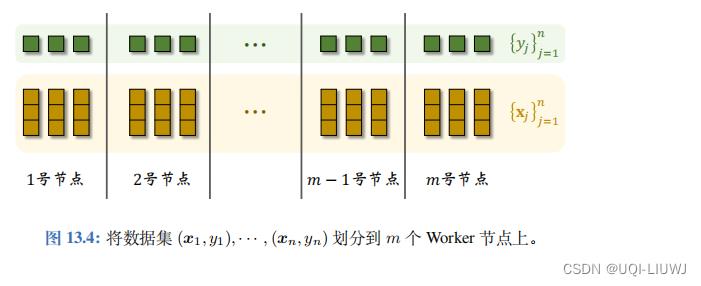 与数据并发相对的是模型并发 (Model Parallelism) ， 即将模型参数 w 划分到 m 个 Worker 节点上；每个节点有全部数据，但是只有一部分模型参数。

4 数据并发下并行梯度下降的流程

用数据并发，设集合是集合 1 , 2 , · · · , n 的划分； 集合包含第 k 个 Worker 节点上所有样本的序号。 并行梯度下降需要重复——广播、 映射、规约、更新参数——这四个步骤，直到算法收敛。

•  广播 (Broadcast) ： 服务器将当前的模型参数 广播到 m 个 Worker 节点。这样 一来，所有节点都知道。

• 映射 (Map)： 这一步让 m 个 Worker 节点做并行计算，用本地数据计算梯度。需要在编程的时候定义这样一个映射函数：

  • 第 k 号 Worker 节点做如下映射：

•  规约 (Reduce) ： 在做完映射之后，向量分布式存储在 m 个 Worker节点上，每个节点有一个子集。
  • 目标函数 在 处的梯度为：

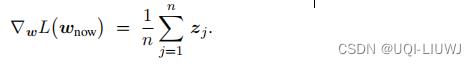
  •   每个Worker节点首先会规约自己本地的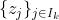，得到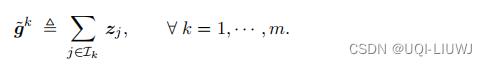

    

  • 然后将发送给服务器，服务器对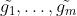求和，再除以n，得到梯度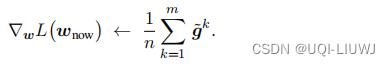

     

  • 先在本地做规约，再做通信，只需要传输 md 个浮点数；如果不先在本地归约，直 接把所有的zj都发送给服务器，那么需要传输 nd 个浮点数，通信代价大得多（m<<n)

• 更新参数： 最后，服务器在本地做梯度下降，更新模型参数：

5  并行计算的代价

5.1 两种时间的定义

5.1.1 钟表时间

钟表时间 (Wall-clock Time) ，也叫 Elapsed Real Time ，意思是程序实际运行的时间。 可以这样理解钟表时间：在程序开始运行的时候，记录下墙上钟表的时刻；在程序 结束的时候，再记录钟表的时刻；两者之差就是钟表时间。

5.1.2 处理器时间

处理器时间 (CPU Time 或 GPU Time) 是所有处理器运行时间的

总和

。 比如使用 4块 CPU 做并行计算，程序运行的钟表时间是 1 分钟，期间 CPU 没有空闲，那么系 统的 CPU 时间等于 4 分钟。

 处理器数量越多，每块处理器承担的计算量就越小，那么程序运行速度就会越快。

所以 并行计算可以让钟表时间更短。

用多个处理器做并行计算，然而总计算量没有减少，因此并行计算不会让处理器时间更短。

5.2 加速比

  通常用 加速比 (Speedup Ratio) 衡量并行计算带来的速度提升。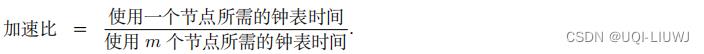

 

通常来说，节点数量越多，算力越强，加速比就越大。 在实验报告中，通常需要把加速比绘制成一条曲线。把节点数量设置为不同的值，比如 m = 1 , 2 , 4 , 8 , 16 , 32 ，得到相应 的加速比。 把 m 作为横轴，把加速比作为纵轴，绘制出加速比曲线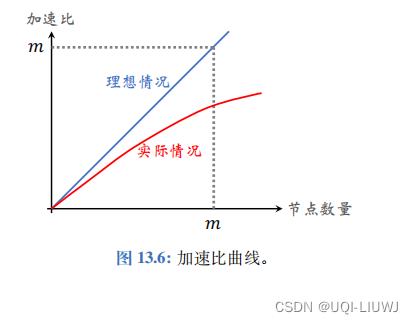

        在最理想的情况下，使用 m 个节 点，每个节点承担的计算量，那么钟表时间会减小到原来的，即加速比等于 m。         图 13.6 中的蓝色直线是理想情况下的加速比。         但实际的加速 比往往是图中的红色曲线，即加速比 小于 m 。         其原因在于计算所需时间只占总的钟表时间的一部分。通信等操作也要花费时间，导致加速比达不到 m 。

 

5.3 影响加速比的因素 

 5.3.1 通信量  

通信量 (Communication Complexity) 的意思是有多少个比特或者浮点数在服务器与 Worker 节点之间传输。

• 在并行梯度下降的例子中，每一轮梯度下降需要做两次通信：
  • 服务器将模型参数广播给 m 个 Worker 节点
  • Worker 节点将计算出的梯度发送给服务器。
  • 因此每一轮梯度下降的通信量都是 O(md)。

通信量越大，通信花费的时间越长，加速比越小

5.3.2 延迟

延迟 (Latency) 是由计算机网络的硬件和软件系统决定的。 做通信的时候，需要把大的矩阵、向量拆分成小数据包，通过计算机网络逐个传输数据包。 即使数据包再小，从发送到接收之间也需要花费一定时间，这个时间就是延迟。 通常来说，

延迟与通信次数成正比，而跟通信量关系不大。

5.3.3 通信时间

通信时间 主要由通信量和延迟造成。我们无法准确预估通信时间（指的是钟表时间）， 除非实际做实验测量。但我们不妨用下面的公式粗略估计通信时间：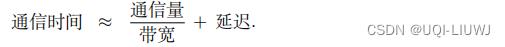

 

在并行计算中，通信时间是不容忽视的，通信时间甚至有可能超过计算时间。

降低通信

量和通信次数是设计并行算法的关键

。只有当通信时间远低于计算时间，才能取得较高 的加速比。