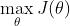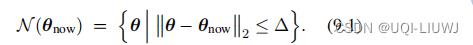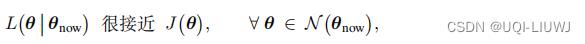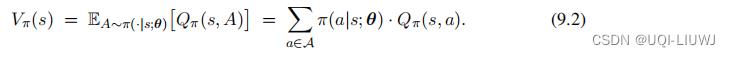强化学习笔记：置信域策略优化 TRPO

Posted 2022-05-30 UQI-LIUWJ

• 置信域策略优化 (Trust Region Policy Optimization, TRPO) 是一种策略学习方法，跟其他策略梯度有很多相似之处。
• 跟策略梯度方法相比，TRPO 有两个优势：
  • 第一，TRPO表现更稳定，收敛曲线不会剧烈波动，而且对学习率不敏感；
  • 第二，TRPO 用更少的经验（即智能体收集到的状态、动作、奖励）就能达到与策略梯度方法相同的表现。

1 置信域方法

假设我们有这样的一个优化问题：

有各种各样的优化算法用于解决这个问题。几乎所有的数值算法都是做这样的迭代

不同的优化算法，其区别在于，具体怎么样利用数据来更新变量θ

 置信域方法用到“置信域”这一个概念。

给定当前变量，我们用来表示的邻域：

 

置信域方法则是需要构造一个函数，这个函数需要满足： 

 

那么集合称为置信域。

顾名思义，在的邻域上，我们可以用来代替目标函数J(θ)

 1.1 举例

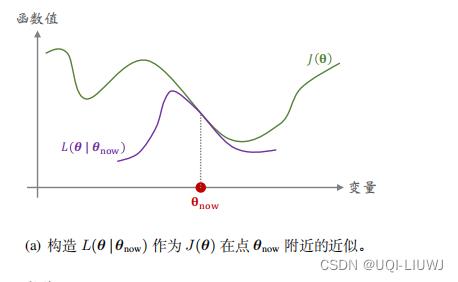
我们用一个一元函数的例子来解释J(θ)和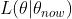之间的关系：

• 上图中横轴是优化变量θ，纵轴是函数值
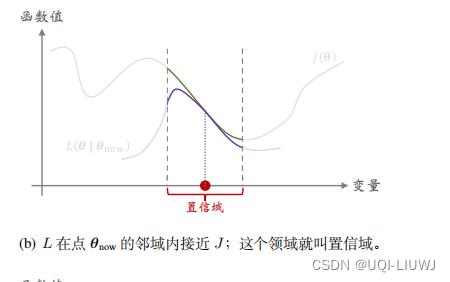
• 如图所示，函数未必在整个定义域上都接近J(θ)，只是在 的邻域上接近
• 这个邻域 称为置信域

•  通常来说，J 是个很复杂的函数，我们甚至可能不知道 J 的解析表达式
• 而我们人为构造出的函数 L 相对较为简单，比如 L 是 J 的蒙特卡洛近似，或者是 J 在 这个点的二阶泰勒展开。

• 既然可以信任 L ，那么不妨用 L 代替复杂的函数 J ，然后对 L 做最大化。这样比直接优化 J 要容易得多。 ——>这就是置信域方法 的思想。

具体来说，置信域方法做下面这两个步骤，一直重复下去，当无法让 J 的值增大的时候终止算法

•  第一步：做近似
  • 给定，构造函数，使得在上的所有θ，函数值和J(θ)足够接近（如上图的(b)）
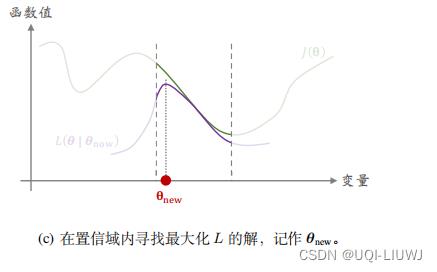
• 第二步：最大化
  • 在置信域中寻找变量θ的值，使得函数L的值最大化
  • 我们记找到的值为

  

• 置信域方法其实是一类算法框架，而非一个具体的算法。
• 有很多种方式实现实现置 信域方法。
  • 第一步需要做近似，而做近似的方法有多种多样，比如蒙特卡洛、二阶泰勒展开。
  • 第二步需要解一个带约束的最大化问题；求解这个问题又需要单独的数值优化算法，比如梯度投影算法、拉格朗日法。
  • 除此之外，置信域也有多种多样的选择

2 策略学习（复习）

对于策略网络，我们记动作价值函数为，他是回报的期望。

状态价值函数我们记作：

 策略网络学习的目标函数是：

 

强化学习笔记：policy learning_UQI-LIUWJ的博客-CSDN博客中提到的REINFORCE和Actor-Critic使用不同的方法，通过蒙特卡洛近似梯度，得到随机梯度，然后使用随机梯度上升来更新θ

3  TRPO的目标函数 

我们把目标函数J(θ)变换成另一种等价形式。

我们改写一下状态价值函数：

 

 4 TRPO 数学推导

TRPO 是 置信域方法在策略学习中的应用，所以 TRPO 也遵循置信域方法的框架——重复 做近似 和 最大化这两个步骤，直到算法收敛。 收敛指的是无法增大目标函数 J ( θ ) ，即无法增大期望回报。

4.1 做近似

• 我们从定理 9.1 出发。定理把目标函数 J(θ) 写成了期望的形式。
• 我们无法直接算出期望，无法得到 J(θ) 的解析表达式；
  • 原因在于只有环境知道状态S 的概率密度函数，而我们不知道。
• 我们可以对期望做蒙特卡洛近似，从而把函数 J 近 似成函数 L 。
• 用策略网络 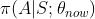控制智能体和环境的交互，从头到尾玩一局游戏，观测到一条轨迹：
  • 
  • 此时的动作at都是根据策略网络 抽取得到的样本
• 所以 是对定理9.1 中期望的无偏估计

• 我们观测到了n组状态和动作，于是我们记得到的均值为：

• 这个均值L也是无偏估计，可以作为目标函数J的蒙特卡洛近似

• 但我们此时还是不知道动作价值

  • 我们可以将其近似成观测到的折扣回报ut  

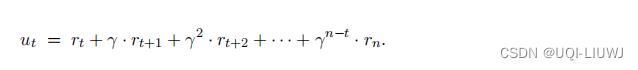
•  用ut代替，于是此时9.6式变成了：

（我们是求使得L最大的θ，所以有没有前面的1/n都无所谓）

4.2 最大化

•  在4.1中，我们用

来近似目标函数J(θ)

•  我们现在需要做的就是求解θ，使之满足：
• 下一个问题就是，该使用什么样的置信域呢？
  • 一种方法是用以 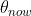为球心、以 ∆ 为半径的球作为置信域。
    • 这样的话，公式9.8就变成了：
    • 

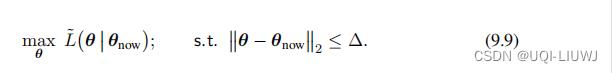
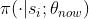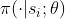  • 另一种方法是用 KL 散度衡量两个概率质量函数和的距离
    • 两个概率质量函数区别越大，它们的 KL 散度就越大。 
    •  反之，如果 θ 很接近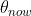，那他们的KL散度就会很接近
    • 这样的话，公式9.8就变成 

  • 用球作为置信域的好处是置信域是简单的形状，求解最大化问题比较容易，但是用球做 置信域的实际效果不如用 KL 散度。
• but，9.9 或9.10的求解其实并不容易。。。。

5 流程总结

TRPO 需要重复 做

近似

和 最大化 这两个步骤： 

 

 

 但往往第二步实现起来很麻烦。。。

还有一个和策略网络不同的地方是：策略网络用蒙特卡洛近似的是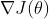 ,TRPO用蒙特卡洛近似的直接是J(θ）

5.1 TRPO的超参数

        相比于一般的策略网络，TRPO需要调的超参数会多一个：除了梯度上升过程需要调的学习率之外，置信域的半径Δ也是需要手动调整的

        通常来说，Δ在算法运行过程中要逐渐缩小。

        不过，虽然TRPO需要调参，但是它对超参数的设置不敏感（也就是说，即使超参数设置得不够好，TRPO的表现也不会太差）【相比而言，策略梯度算法对于超参数则更加敏感】