动态规划_二项式系数

Posted 2020-11-18 passion-sky

动态规划之二项式系数

@(算法学习)

(nk)=n!(n?k)!k!

计算二项式系数的问题在于，系数本身在int表示范围内，但是计算用到的分子是阶乘，这个是很大的数，会导致溢出的问题。

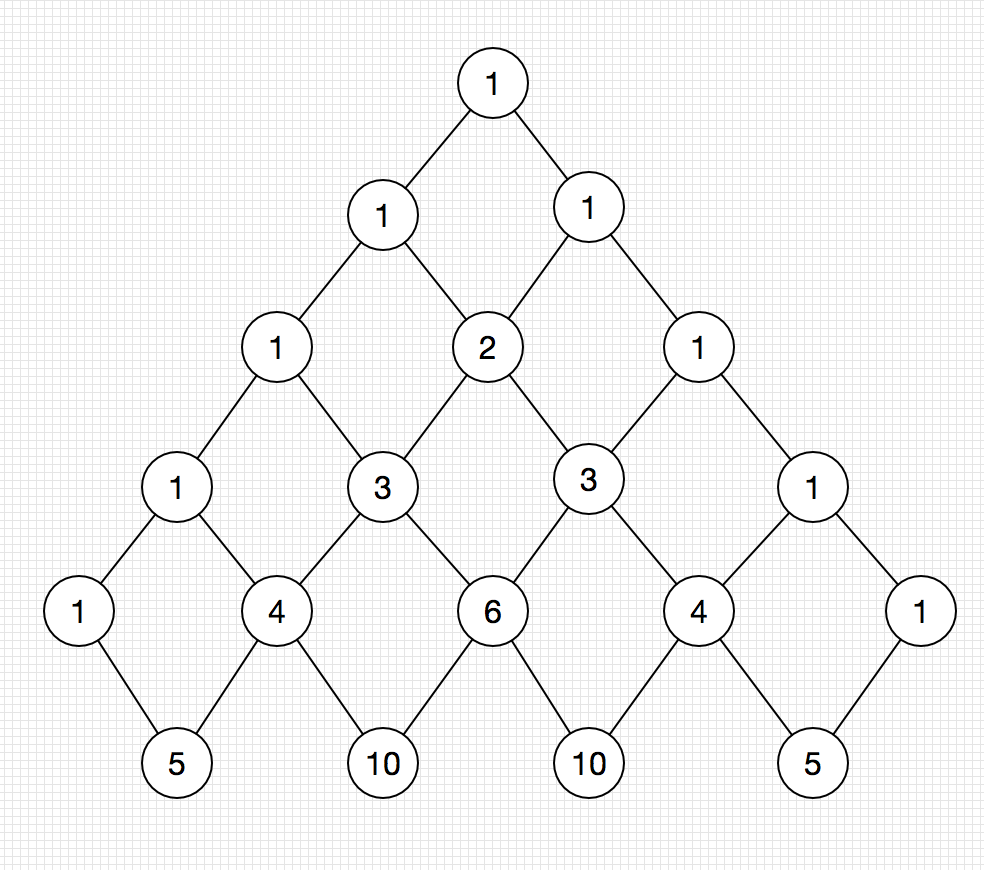
所以，比较好的计算方法是运用帕斯卡三角形总结的规律求解。

第一行表达的是：(00)=1

第二行表达的是：(10)=1,(11)=1
第三行表达的是：(20)=1,(21)=2,(22)=1

…

更有趣的是，每一个数是肩头两个数字之和。

运用的规律是：(nk)=(n?1k?1)+(n?1k)

，这个翻译成中文很好理解。从n个东西中选取k个，在面对第k件东西时，有一个决策，这件不选或者选两条路径。选了第k件则从剩下的n-1件里选k-1件即可。如果不选，就要从剩下的n-1件中选择k件。

这个思想在背包问题中运用的尤其广泛。背包问题是动态规划问题的一种模型，因此，也可以侧面反映动态规划的思想。

#include <stdio.h>

#define MAXN 100

long binomial_coefficient(int n, int m)// 从n中选择m
{
    int i,j;
    long bc[MAXN][MAXN]; //二项式系数表
    for(i = 0; i <= n; i++) //帕斯卡三角每行第一个数全是1
    {
        bc[i][0] = 1;
    }
    for(j = 0; j <= n; j++) // 帕斯卡三角每行最后一个数全是1
    {
        bc[j][j] = 1;
    }

    for(i = 1; i <= n; i++) //状态转移方程
    {
        for(j = 1; j < i; j++)
        {
            bc[i][j] = bc[i-1][j-1]+bc[i-1][j];
        }
    }
    return bc[n][m];
}
int main()
{
    int n, m;
    while(scanf("%d%d",&n,&m))
    {
        int res = binomial_coefficient(n,m);
        printf("Result =  %d
", res);
    }

    return 0;
}