二叉树遍历
Posted hzb462606
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了二叉树遍历相关的知识,希望对你有一定的参考价值。
这里写的是最简单的二叉树遍历,最简单的定义,为的是清晰,一目了然。
首先:Tree.java--》
package 二叉树遍历; @SuppressWarnings("all") public class Tree { //定义根值 private String value; private Tree left; private Tree right; /** * 功能:定义一个二叉树,然后进行3种方式的遍历. * 构造的二叉树: * 1 * / * 2 3 * / / * 4 5 6 7 * / * 8 9 * 先序遍历:DLR * 1 2 4 8 9 5 3 6 7 * 中序遍历:LDR * 8 4 9 2 5 1 6 3 7 * 后序遍历:LRD * 8 9 4 5 2 6 7 3 1 */ public Tree createTree() { //定义最上层根节点 this.value="1"; //定义最上层根节点-->左子树 this.left=new Tree(); Tree left1=this.left; //深度2 left1.value="2"; left1.left=new Tree(); left1.right=new Tree();
//深度3 Tree left1_left2=left1.left; Tree left1_right2=left1.right; left1_left2.value="4"; left1_right2.value="5"; left1_left2.left=new Tree(); left1_left2.right=new Tree(); //深度4 Tree left2_left3=left1_left2.left; Tree left2_right3=left1_left2.right; left2_left3.value="8"; left2_right3.value="9"; //定义最上层根节点-->右子树 this.right=new Tree(); Tree right1=this.right;
//深度2 right1.value="3"; right1.left=new Tree(); right1.right=new Tree(); //深度3 Tree right1_left1=right1.left; Tree right1_right1=right1.right; right1_left1.value="6"; right1_right1.value="7"; return this; } //前序遍历 public void beforeFindData(Tree tree) { if(tree!=null) { System.out.print(tree.value+" "); beforeFindData(tree.left); beforeFindData(tree.right); }else { return; } } //中序遍历 public void contreFindData(Tree tree) { if(tree!=null) { contreFindData(tree.left); System.out.print(tree.value+" "); contreFindData(tree.right); }else { return; } } //后序遍历 public void afterFindData(Tree tree) { if(tree!=null) { afterFindData(tree.left); afterFindData(tree.right); System.out.print(tree.value+" "); }else { return; } } }
测试用例:TreeTest.java-->
package 二叉树遍历; public class TreeTest { public static void main(String args[]) { Tree t=new Tree().createTree(); System.out.print("前序遍历:-->"); t.beforeFindData(t); System.out.println(""); System.out.print("中序遍历:-->"); t.contreFindData(t); System.out.println(""); System.out.print("后序遍历:-->"); t.afterFindData(t); System.out.println(""); } }
结果:
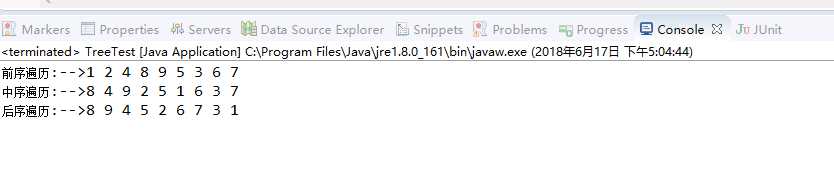
以上是关于二叉树遍历的主要内容,如果未能解决你的问题,请参考以下文章