matlab计算铰接式履带车辆转向性能
Posted studyer_domi
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了matlab计算铰接式履带车辆转向性能相关的知识,希望对你有一定的参考价值。
1、内容简介
234
2、内容说明
1.履带车辆转向运动学模型
1.1假设条件
根据研究问题需要作如下假设
1)车辆在水田行进中采用低速转向,因此车辆转向过程中不考虑离心力对转向性能的影响。
2)行驶转向过程中车辆始终作匀速稳态转向运动且车体质心与车辆的几何中心始终重合。
3)履带接地段压力为连续线性分布,不计履带张力变化对接地段压力的影响。
4)车辆转向过程忽略履带侧面推土阻力。
5)车辆履带轮偏转角满足阿克曼转角关系。
1.2坐标系描述
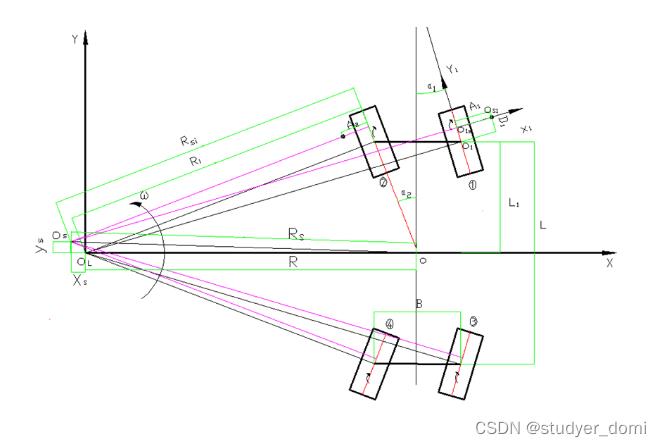
该示意图表示的四履带车辆的转向方式为逆向位转向方式,后履带轮的偏转方向与前轮相反,履带车辆转向时,每条履带各有其接地段速度瞬心,(为履带轮标号),横向作用力使相对履带接地段几何中心产生纵向偏移量,履带的滑转、滑移使与 之间出现横向偏移量,履带接地段速度瞬心的纵向偏移使车辆实际转向中心偏离理论转向中心。如图1所示,在水平地面上建立为原点的地面惯性坐标系,并分别建立以履带轮建立接地段中心线上的为原点的局部连体坐标系 。为车辆质心(几何中心),车辆以角速度绕实际转向中心做逆时针匀速转向运动。为各履带轮实际转向半径,为各履带轮理论转向半径,分别为理论转向中心与实际转向中心沿地面坐标系方向的横向与纵向位移,L为车辆轴距。
2.1转向运动学分析
根据剪切应力与位移关系可得,履带接地段上任意一点的剪切应力与该点的剪切位移有关,履带轮受到的横向与纵向作用力都是由接地履带对地面产生剪切作用产生的驱动力引起的,因此可以通过对接地履带上任意一点的滑动速度进行积分得到其剪切位移量,从而获得剪切应力。
由运动学分析可得,当车辆以角速度绕转向中心作匀速稳态转向运动时,履带轮的运动是由牵连运动和相对运动构成的复合运动,与在履带接地段中心线上的点对应的履带接地段在连体坐标系下方向的牵连速度为
公式 1
则与在两侧履带接地段中心线上的点对应的履带接地段在连体坐标系下方向的相对速度为
公式 2。
式中:为驱动轮节圆半径;为驱动轮角速度。
当履带没有滑转和滑移时,履带接地段的瞬时转向中心与履带接地段几何中心重合,此时在该点处的相对速度等于牵连速度,该点的绝对速度为0
当存在滑转和滑移时,点处在连体坐标系下方向的绝对速度即为该点的纵向滑动速度,其表达式为
公式 3
式中为履带轮转向极的横向偏移量。
图表 2
图表2为履带轮接地段受力与速度分析图,对于履带接地段上的任意一点,其在连体坐标系下的纵向滑动速度与点相同,即为,同样对于点,履带接地段上对应于点 处的相对速度在连体就坐标系下的横向分量为,也即为点在连体坐标系下的横向滑动速度
公式 4
根据坐标转换关系,车辆连体坐标到地面惯性坐标系的方向余弦矩阵为
公式 5
根据坐标变换关系,在地面参考坐标系下,点的横向及纵向滑动速度表示为
公式 6
由于履带车辆以角速度做匀速转向运动,且点到履带接地最前端的距离为,则当履带接地段最前端运动到点时车辆的转向角φ为
公式 7
式中:
为履带车辆做稳态匀速转向时履带接地段最前端运动到点时所需的时间;
为履带接地长度;
公式 8
2.2车辆转向半径关系
车辆四个履带轮的偏转角满足如下关系
,公式 9
公式 10
车辆内外侧履带轮偏转角满足如下阿克曼转角关系
公式 11
转向时,内侧前轮偏转角最大为
履带轮①与履带轮②的实际转向半径与为
,, 公式 12
履带轮③与履带轮④的实际转向半径与为
,, 公式 13
由作图得
所以车辆最小实际转弯半径为
公式 14
各条履带轮的理论转向半径为:
, 公式 15
公式 16
因此为方便表示,用标号为3的履带轮的理论转弯半径为
公式 17
以车辆车架几何中心O为质心,以之间的距离作为整车理论转向半径R,为方便计算以履带轮②的偏转角来表示
公式 18
车辆几何中心O到实际转向中心的距离,即车辆实际转向半径,为方便计算以履带轮②的偏转角来表示
公式 19
由于车辆几何中心O到实际转向中心的距离也可表达为下式
公式 20
由公式18,19,20得
公式 21
各条履带接地面纵向偏移可以表达为公式22
公式 22
车辆转向角速度v为2m/s(车辆几何中心处速度为基准点)
车辆转向角速度为
公式 23
每个履带驱动轮角速度为
公式 24
2.3履带接地段的剪切位移
履带接地段上各点的剪切位移沿着接地长度方向累积,至接地段后端达到最大值。
由于履带接地段纵向中心线上的每一点的纵向及横向滑动速度均不同,根据定义点处剪切变形量的横向分量和纵向分量分别表示为点的横向及纵向滑动速度在履带接地段最前端运动到点所花时间的积分,其表达式为
公式 25
公式 26
则点处的合成剪切位移量为
公式 27
2.3履带与土壤之间的相互作用力
如图表2所示,履带车辆在行驶过程中履带与土壤发生剪切作用,根据莫尔土壤剪切理论,履带接地段任意一点处土壤剪切应力为
公式 28
公式 29
式中:为履带与土壤之间的剪切应力, ;为履带接地面积, ;为土壤内聚力系数, ;为履带接地压力,;为土壤内摩擦角,为土壤抗剪模量,;为土壤剪切变形量, ,为履带宽度,
如图2所示为履带接地段上的任意一点,,分别为点的横向及纵向滑动速度, 、 分别为点单位面积上受到的切向力。
为履带接地段上任一点处的滑动速度与轴正方向的夹角。
公式 30
公式 31
在局部随动坐标系下,在轴轴上的分量分别为
公式 32
公式 33
由于履带-地面之间的剪切位移及剪切应力在履带接地长度上并不相同,剪切应力横向分量不仅产生切向力的横向分量,而且还形成绕履带点的转向阻力矩,其表达式为:
公式 34
由公式32,公式33可得,接地履带的横向作用力和纵向作用力为:
公式 35
公式 36
履带驱动力为 公式 37
车辆总驱动力F为
公式 38
由公式34得单条履带转向阻力矩为
公式 39
当履带车辆以2m/s速度,偏转角度为20度转向时,各履带受到的剪切阻力计算结果如下表
履带1
履带2
履带3
履带4
2.4履带接地面瞬心的横向偏移是由驱动履带滑转或从动履带滑移引起的。履带运动包括履带对履带架的相对运动卷绕和履带环与车体一起的牵连运动即平动速度。履带行走装置转向时,牵连运动指车辆绕转向中心的旋转运动。滑转发生在履带的相对运动速度(即卷绕速度) 大于牵连运动速度(即平动速度时),而滑移发生在相对运动速度小于牵连运动速度时。为此,引入履带运动的滑转率概念
滑转率 可用于定量描述履带接地面滑转或滑移的程度大小
履带的卷绕速度, 可表示为
履带的滑转率可表示为
3、仿真分析
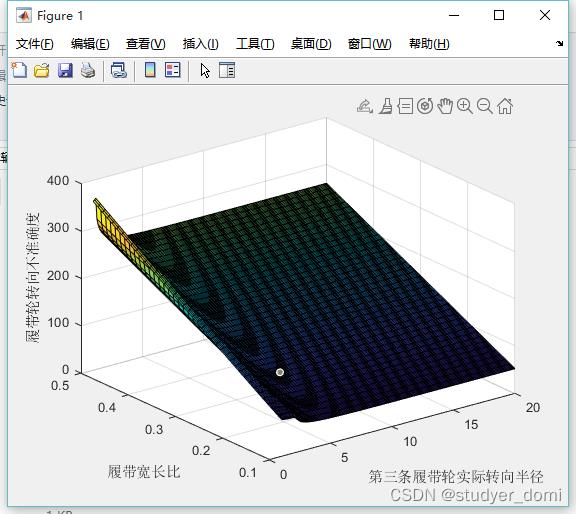
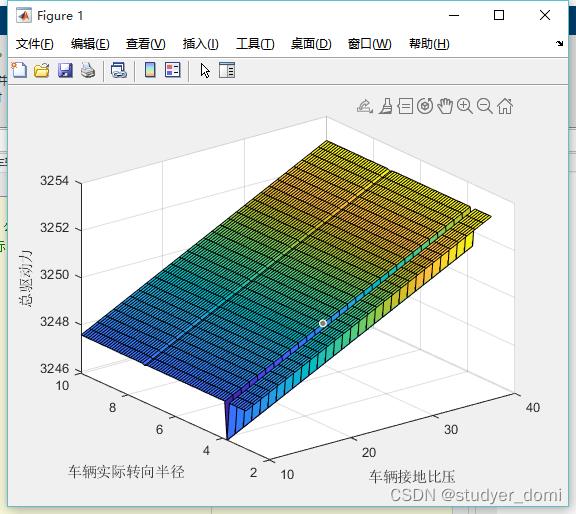
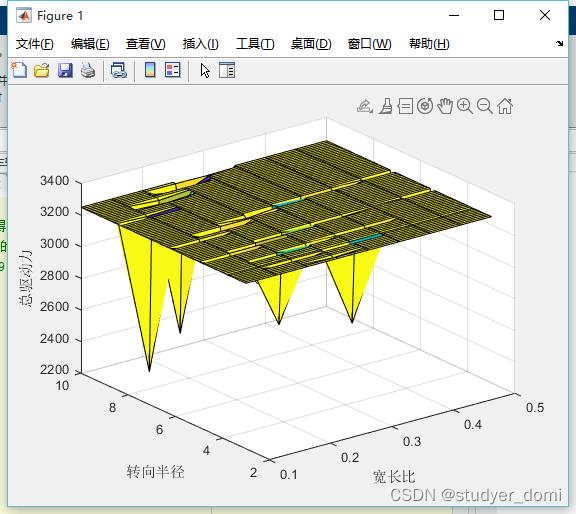
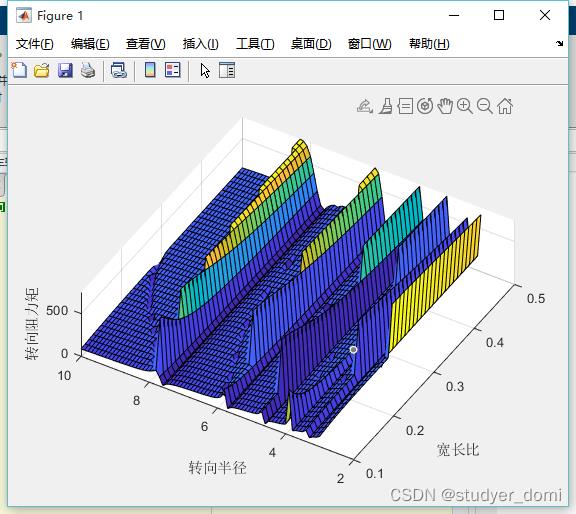
4、参考论文
基于剪应力模型的履带车辆转向力矩分析与试验_芮强.pdf
多履带行走装置关键设计技术研究_李勇.caj
多履带车辆转向性能分析_王国强.caj
履带车辆软地面稳态转向驱动力计算模型_曹付义.caj
履带车辆软地面行驶性能研究_胡际勇.caj
考虑土壤剪切变形的铰接式履带车辆转向性能_董超.pdf
答1疑2咨3询4企q鹅q号:1762016542

以上是关于matlab计算铰接式履带车辆转向性能的主要内容,如果未能解决你的问题,请参考以下文章