PyTorch自动求导：反向传播的一切

Posted 2022-05-11 人邮异步社区

在之前的介绍中，我们看到了一个简单的反向传播的例子：通过使用链式规则反向传播导数，我们计算了模型和损失的复合函数关于其内部参数w和b的梯度。这里的基本要求是我们处理的所有函数都是可微的。如果满足该基本要求，我们就可以计算梯度，我们之前称之为“损失变化率”，它是相对一次扫描的参数而言的。

即使我们有一个包含数百万个参数的复杂模型，只要我们的模型是可微的，计算关于参数的损失梯度就是写出导数的解析表达式并计算一次。当然，写一个非常深的线性和非线性函数的导数的解析表达式并不是很有趣，同时该表达式运行得也不会特别快。

5.5.1　自动计算梯度

这时PyTorch张量就会发挥作用（使用名为autograd的PyTorch组件）。第3章全面介绍了张量以及我们可以调用的相关函数。然而，我们忽略了非常有趣的一点：PyTorch张量可以记住它们自己从何而来，根据产生它们的操作和父张量，它们可以根据输入自动提供这些操作的导数链。这意味着我们不需要手动推导模型，给定一个前向表达式，无论嵌套方式如何，PyTorch都会自动提供表达式相对其输入参数的梯度。

1．应用自动求导

此时，最好的方法之一是重写我们的温度计校准代码，这次使用自动求导，看看会发生什么。首先，我们回顾一下我们的模型和损失函数，见代码清单5.1。

代码清单5.1　code/p1ch5/2_autograd.ipynb

# In[3]:
def model(t_u, w, b):
    return w * t_u + b

# In[4]:
def loss_fn(t_p, t_c):
    squared_diffs = (t_p - t_c)**2
    return squared_diffs.mean()

让我们再一次初始化一个参数张量：

# In[5]:
params = torch.tensor([1.0, 0.0], requires_grad=True)

2．使用grad属性

注意到张量构造函数的requires_grad=True参数了吗？这个参数告诉PyTorch跟踪由对params张量进行操作后产生的张量的整个系谱树。换句话说，任何将params作为祖先的张量都可以访问从params到那个张量调用的函数链。如果这些函数是可微的（大多数PyTorch张量操作都是可微的），导数的值将自动填充为params张量的grad属性。

通常，所有PyTorch张量都有一个名为grad的属性。通常情况下，该属性值为None：

# In[6]:
params.grad is None

# Out[6]:
True

我们所要做的就是从一个requires_grad为True的张量开始，调用模型并计算损失，然后反向调用损失张量：

# In[7]:
loss = loss_fn(model(t_u, *params), t_c)
loss.backward()

params.grad

# Out[7]:
tensor([4517.2969, 82.6000])

此时，params的grad属性包含关于params的每个元素的损失的导数。

当我们计算损失时，参数w和b需要计算梯度。除了执行实际的计算外，PyTorch还创建了以操作（黑色圆圈）为节点的自动求导图，如图5.10上部所示。当我们调用loss.backward()时，PyTorch将反向遍历此图以计算梯度，如图5.10下部所示。

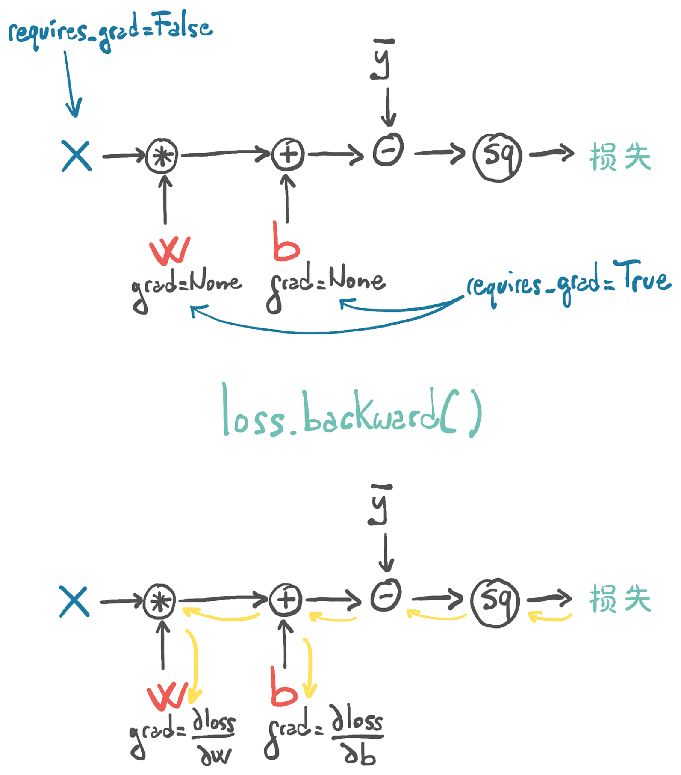
图5.10　执行自动求导计算得到模型的前向图和后向图

3．累加梯度函数

我们可以有任意数量的requires-grad为True的张量和任意组合的函数。在这种情况下，PyTorch将计算整个函数链（计算图）中损失的导数，并将它们的值累加到这些张量的grad属性中（图的叶节点）。

注意，这是许多PyTorch初学者以及一些有经验的人经常会弄错的，我们在这里要强调的是导数是累加存储到grad属性中的。

注意　
调用backward()将导致导数在叶节点上累加。使用梯度进行参数更新后，我们需要显式地将梯度归零。

让我们一起复述一遍：调用backward()将导致导数在叶节点上累加，因此如果提前调用backward()，则会再次计算损失，再次调用backward()（就像在任何训练循环中一样），每个叶节点上的梯度将在上一次迭代中计算的梯度之上累加（求和），这会导致梯度计算不正确。

为了防止这种情况发生，我们需要在每次迭代时明确地将梯度归零。我们可以就地使用zero()_方法轻松地完成这一任务：

# In[8]:
if params.grad is not None:
    params.grad.zero_()

注意　
你可能会好奇为什么梯度的归零是一个必要的步骤，而不是当我们调用backward()时自动进行归零。这样做为在复杂模型中使用梯度提供了更多的灵活性和控制力。

有了这些提醒，让我们看看自动求导训练代码从头到尾是什么样的：

# In[9]:
def training_loop(n_epochs, learning_rate, params, t_u, t_c):
    for epoch in range(1, n_epochs + 1):
        if params.grad is not None:    ⇽---  这可以在循环中调用loss.backward()之前的任何时间完成
            params.grad.zero_()

        t_p = model(t_u, *params)
        loss = loss_fn(t_p, t_c)
        loss.backward()

        with torch.no_grad():    ⇽---  这是一段有点儿烦琐的代码，但是正如我们将在5.5.2小节中看到的那样，这在实践中不是一个问题
            params -= learning_rate * params.grad

        if epoch % 500 == 0:
            print('Epoch %d, Loss %f' % (epoch, float(loss)))

    return params

注意，params并不像我们预期的那样简单，其有2个特殊性。首先，我们使用Python的with语句将更新封装在非梯度上下文中，这意味着在with块中，PyTorch自动求导机制将不起作用[9]：也就是说，不向前向图添加边。实际上，当我们执行这段代码时，PyTorch记录的前向图在我们调用backward()时被消费掉，留下params叶节点。但是现在我们想在叶节点建立一个新的前向图之前改变它。虽然这个例子通常被封装在我们在5.5.2小节所讨论的优化器中，但是当我们在5.5.4小节中看到no_grad()的另一种常见用法时我们还会做进一步讨论。

其次，我们在适当的地方更新params张量，这意味着我们保持相同的params张量但从中减去更新。当使用自动求导时，我们通常避免就地更新，因为PyTorch的自动求导引擎可能需要我们修改反向传播的值。然而，在这里，我们没有自动求导操作，保持params张量是有益的。当我们在5.5.2小节中向优化器注册参数时，不通过为其变量名分配新的张量来替换参数将变得至关重要。

让我们看看它是否有效：

# In[10]:
training_loop(
    n_epochs = 5000,
    learning_rate = 1e-2,
    params = torch.tensor([1.0, 0.0], requires_grad=True),    ⇽---  添加requires_grad=True是关键
    t_u = t_un,    ⇽---  同样，我们用的是归一化的t_un，而不是t_u
    t_c = t_c)

# Out[10]:
Epoch 500, Loss 7.860116
Epoch 1000, Loss 3.828538
Epoch 1500, Loss 3.092191
Epoch 2000, Loss 2.957697
Epoch 2500, Loss 2.933134
Epoch 3000, Loss 2.928648
Epoch 3500, Loss 2.927830
Epoch 4000, Loss 2.927679
Epoch 4500, Loss 2.927652
Epoch 5000, Loss 2.927647

tensor([  5.3671, -17.3012], requires_grad=True)

结果和我们之前得到的是一样的。这意味着，虽然我们有能力手动计算导数，但我们不再需要这样做。

5.5.2　优化器

在示例代码中，我们使用了批量梯度下降（vanilla[10]）进行优化，这在我们的简单例子中运行良好。毋庸置疑，有一些优化策略和技巧可以帮助收敛，特别是当模型变得复杂时。

我们将在后文深入探讨这个主题，但是现在是时候介绍PyTorch从用户代码中提取优化策略的方法了（也就是我们检查过的训练循环），这就避免了我们必须自己更新模型中的每个参数的烦琐工作。

torch模块有一个optim子模块，我们可以在其中找到实现不同优化算法的类。以下是一个简要列表（code/p1ch5/ 3_optimizers.ipynb）：

# In[5]:
import torch.optim as optim

dir(optim)

# Out[5]:
['ASGD',
 'Adadelta',
 'Adagrad',
 'Adam',
 'Adamax',
 'LBFGS',
 'Optimizer',
 'RMSprop',
 'Rprop',
 'SGD',
 'SparseAdam',
...
]

每个优化器构造函数都接收一个参数列表（又称PyTorch张量，通常将requires_grad设置为True）作为第1个输入。传递给优化器的所有参数都保留在优化器对象中，这样优化器就可以更新它们的值并访问它们的grad属性，如图5.11所示。

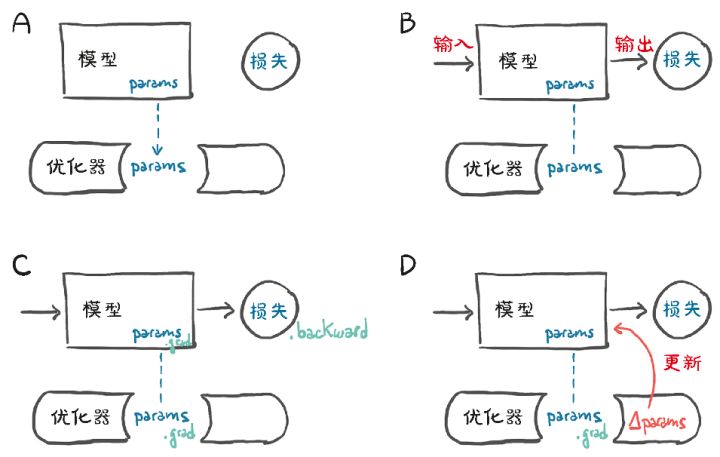
图5.11　（A）优化器如何保持对参数引用的概念表示；（B）从输入中计算出损失后；（C）调用.backward导致.grad被填充到参数中；（D）此时，优化器可以访问.grad并计算参数更新

每个优化器公开2个方法：zero_grad()和step.zero_grad()，在构造函数中将传递给优化器的所有参数的grad属性归零。step()根据特定优化器实现的优化策略更新这些参数的值。

1．使用一个梯度下降优化器

让我们创建params张量并实例化一个梯度下降优化器：

# In[6]:
params = torch.tensor([1.0, 0.0], requires_grad=True)
learning_rate = 1e-5
optimizer = optim.SGD([params], lr=learning_rate)

这里SGD代表随机梯度下降。只要动量因子momentum参数设置为0.0，该参数默认值也是0.0，那么优化器本身也是一种批量梯度下降算法。“随机”一词来自这样一个事实，即梯度通常是通过对所有输入样本的一个随机子集（称为小批量）取平均值而得到的。然而，优化器不知道损失是在所有样本（批量）上评估的，还是在它们的随机子集（随机）上评估的，所以在这2种情况下，算法实际上是相同的。

不管怎样，让我们来看看我们的新优化器：

# In[7]:
t_p = model(t_u, *params)
loss = loss_fn(t_p, t_c)
loss.backward()

optimizer.step()

params

# Out[7]:
tensor([ 9.5483e-01, -8.2600e-04], requires_grad=True)

params的值在调用step()时更新，而不需要我们自己去操作！即优化器会查看params.grad并更新params，从中减去学习率乘梯度，就像我们以前手动编写的代码一样。

在将这段代码放入一个训练循环之前，我们需要把梯度归零。

如果我们在一个循环中调用前面的代码，梯度就会在每次调用backward()时在叶节点中累加，那么我们的梯度下降就会遍布整个循环区域！下面是准备循环的代码，在适当的位置即在调用backward()之前对zero_grad()的调用。

# In[8]:
params = torch.tensor([1.0, 0.0], requires_grad=True)
learning_rate = 1e-2
optimizer = optim.SGD([params], lr=learning_rate)

t_p = model(t_un, *params)
loss = loss_fn(t_p, t_c)

optimizer.zero_grad()    ⇽---  与前面一样，这个调用有些随意，它也可能是在循环的早期被调用
loss.backward()
optimizer.step()

params

# Out[8]:
tensor([1.7761, 0.1064], requires_grad=True)

完美！看看optim模块如何帮助我们抽象出特定的优化方案？我们所要做的就是向它提供一个参数列表（这个列表可能非常长，这是深度神经网络模型所需要的）。

让我们相应地更新我们的训练循环：

# In[9]:
def training_loop(n_epochs, optimizer, params, t_u, t_c):
    for epoch in range(1, n_epochs + 1):
        t_p = model(t_u, *params)
        loss = loss_fn(t_p, t_c)

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        if epoch % 500 == 0:
           print('Epoch %d, Loss %f' % (epoch, float(loss)))

    return params

# In[10]:
params = torch.tensor([1.0, 0.0], requires_grad=True)
learning_rate = 1e-2
optimizer = optim.SGD([params], lr=learning_rate)    ⇽---  

training_loop(
    n_epochs = 5000,
    optimizer = optimizer,
    params = params,    ⇽---  2个params都是同一个对象很重要，否则优化器不知道模型使用了什么参数
    t_u = t_un,
    t_c = t_c)

# Out[10]:
Epoch 500, Loss 7.860118
Epoch 1000, Loss 3.828538
Epoch 1500, Loss 3.092191
Epoch 2000, Loss 2.957697
Epoch 2500, Loss 2.933134
Epoch 3000, Loss 2.928648
Epoch 3500, Loss 2.927830
Epoch 4000, Loss 2.927680
Epoch 4500, Loss 2.927651
Epoch 5000, Loss 2.927648

tensor([  5.3671, -17.3012], requires_grad=True)

同样，我们得到了和之前一样的结果。这进一步证实了虽然我们知道如何手动降低梯度，但我们不再需要这样做。

2．测试其他优化器

为了测试其他优化器，我们所要做的就是实例化一个不同的优化器，如Adam，而不是SGD。代码的其余部分保持原样。

关于Adam优化器，我们将不介绍过多细节。它是一个更复杂的优化器，其中学习率是自适应设置的。此外，它对参数的缩放不太敏感——以至于我们可以使用原始的（非归一化的）输入t_u，甚至可以将学习率提高到1e-1。

# In[11]:
params = torch.tensor([1.0, 0.0], requires_grad=True)
learning_rate = 1e-1
optimizer = optim.Adam([params], lr=learning_rate)    ⇽---  新的优化器类

training_loop(
    n_epochs = 2000,
    optimizer = optimizer,
    params = params,
    t_u = t_u,    ⇽---  我们使用原始的输入t_u
    t_c = t_c)

# Out[11]:
Epoch 500, Loss 7.612903
Epoch 1000, Loss 3.086700
Epoch 1500, Loss 2.928578
Epoch 2000, Loss 2.927646

tensor([   0.5367, -17.3021], requires_grad=True)

优化器不是我们训练循环中唯一灵活的部分，现在让我们把注意力转向模型。为了在相同的数据和相同的损失上训练神经网络，我们只需要改变模型函数。在这种情况下，这样做并没有什么特别的意义，因为我们知道，将摄氏温度转换为华氏温度等于一个线性变换，但我们还是会在第6章中这样做。我们很快就会看到，神经网络允许我们去除对我们要逼近的函数形状的任意假设。即便如此，我们还是要看看神经网络是如何被训练的，即使其基础过程是高度非线性的（如用一句话描述图像，就像我们在第2章看到的那样）。

我们已经触及了许多基本概念，这些概念将使我们能够训练复杂的深度学习模型，同时了解底层是如何运行的：反向传播估计梯度、自动求导，以及使用梯度下降或其他优化器优化模型的权重，其余的主要是填补空白。

接下来，我们将顺便提一下如何分割我们的样本，因为这为学习更好地控制自动求导建立了一个“完美”的用例。

5.5.3　训练、验证和过拟合

开普勒告诉了我们一件我们还没有讨论的事情，还记得吗？他把部分数据放在一边，以便从独立的观测结果中验证他的模型。这是一件非常重要的事情，尤其是当我们采用的模型（如神经网络）可以潜在地逼近任何形状的函数时。换句话说，一个具有高度适应性的模型将倾向于使用它的许多参数来确保在数据点的损失最小，但是我们不能保证模型远离数据点后或在数据点之间运行良好。毕竟，这就是我们要求优化器做的事情：最小化数据点的损失。可以肯定的是，如果我们有独立的数据点，我们不会将其用来评估我们的损失或沿着它的负梯度下降，因为我们很快会发现，评估这些独立数据点的损失将产生比预期更高的损失。我们已经提到过这种现象，叫作过拟合。

我们应对过拟合的第1个行动就是认识到它可能会发生。为了做到这一点，开普勒在1600年就指出了，我们必须从我们的数据集（验证集）中取出一些数据点，并且只在剩下的数据点（训练集）上拟合我们的模型，如图5.12所示。然后，当我们拟合模型时，我们可以评估训练集和验证集上的损失。当我们试图决定我们是否已经很好地将模型与数据拟合时，我们必须同时考虑二者！

1．评估训练损失

训练损失会告诉我们，我们的模型是否能够完全拟合训练集，换句话说，我们的模型是否有足够的能力处理数据中的相关信息。如果我们的温度计以某种方式使用对数刻度来测量温度，那么我们的线性模型就没有机会拟合这些测量值，也不能为我们提供一个合理的摄氏温度转换值。在这种情况下，我们的训练损失（我们在训练循环中输出的损失）将在接近0的时候停止下降。

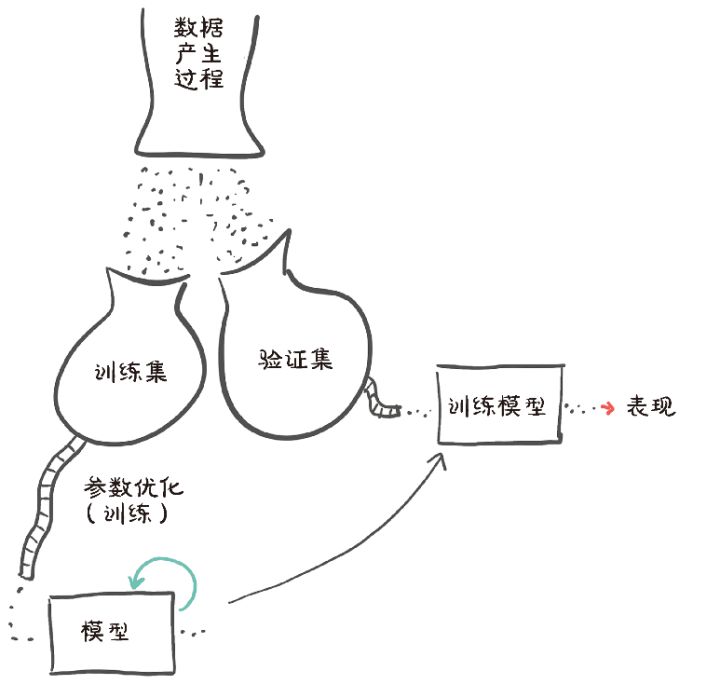
图5.12　数据产生过程、收集和使用训练数据以及独立验证数据的概念表示

深度神经网络可以潜在地近似复杂的函数，前提是神经元的数量和参数足够多。参数的数目越少，我们的网络所能近似的函数的形状就越简单。所以，规则1：如果训练损失没有减少，一种可能是因为模型对数据来说太简单了。训练损失没有减少的另一种可能性是我们的数据没有有意义的信息以让模型对输出做出解释，如果商店里的店员卖给我们一个气压计而不是温度计，即使我们使用魁北克最新的神经网络结构，也几乎不可能仅仅通过气压来预测摄氏温度。

2．推广到验证集

对于验证集呢？如果在验证集中评估的损失没有随着训练集的增加而减少，这意味着我们的模型正在改进它在训练过程中看到的样本的拟合度，但是它不能推广到这个精确数据集之外的样本。一旦我们在新的、先前未见的点上评估模型，损失函数的值就会很差。规则2：如果训练损失和验证损失发散，则表明出现了过拟合现象。

让我们稍微研究一下这个现象。回到温度计的例子，我们决定用一个更复杂的函数来拟合数据，如分段多项式或者一个非常大的神经网络。它可以生成一个蜿蜒通过数据点的模型，如图5.13所示，因为它将损失降到非常接近于0的水平。由于函数远离数据点的行为不会增加损失，因此没有什么可以让模型检查远离训练数据点的输入。

图5.13　这是过拟合的一个极端例子

那么有什么好的解决办法呢？从我们刚才说的来看，过拟合看起来确实是一个问题，它要确保模型在数据点之间的行为对我们试图近似的过程是合理的。首先，我们应该确保我们有足够的数据用于这个过程。如果我们从正弦曲线上采集数据，定期以低频率采样，我们很难拟合一个模型。

如果我们有足够的数据点，我们应该确保能够拟合训练数据的模型在数据点之间尽可能有规律。有几种方法可以实现这一点。一种方法是在损失函数中添加惩罚项，以降低模型的成本，使其表现更平稳、变化更缓慢（直到某一点）。另一种方法是在输入样本中添加噪声，人为地在训练数据样本之间创建新的数据点，并迫使模型也试图拟合这些数据点。还有其他几种方法，它们都与这两种方法有某种关系。但我们能做的最好的事情是让我们的模型更简单，至少能做的第一步是这样的。从直观的角度来看，一个更简单的模型可能不能像一个更复杂的模型那样完美地拟合训练数据，但它可能在数据点之间表现得更有规律。

我们有一些很好的折衷方法。一方面，我们需要模型有足够的能力来拟合训练集。另一方面，我们需要避免模型过拟合。因此，为神经网络模型选择合适的参数的过程分为2步：增大参数直到拟合，然后缩小参数直到停止过拟合。

我们在第12章将会看到更多拟合和过拟合的情况，我们会发现我们的模型是在拟合和过拟合之间寻求平衡。现在回到我们的例子，看看我们如何把数据分割成一个训练集和一个验证集。我们将通过同样的方式打乱t_u和t_c，然后把打乱后的张量分割成2部分。

3．分割数据集

把一个张量的元素打乱，就等于找到一种方法将其元素索引重排列，randperm()函数就是这样做的：

# In[12]:
n_samples = t_u.shape[0]
n_val = int(0.2 * n_samples)

shuffled_indices = torch.randperm(n_samples)

train_indices = shuffled_indices[:-n_val]
val_indices = shuffled_indices[-n_val:]

train_indices, val_indices    ⇽---  由于这些值是随机的，所以如果你得到的值与这里打印的值不一样，也不要感到惊讶

# Out[12]:
(tensor([9, 6, 5, 8, 4, 7, 0, 1, 3]), tensor([ 2, 10]))

我们刚刚得到了索引张量，可以使用索引张量从数据张量开始构建训练集和验证集：

# In[13]:
train_t_u = t_u[train_indices]
train_t_c = t_c[train_indices]

val_t_u = t_u[val_indices]
val_t_c = t_c[val_indices]

train_t_un = 0.1 * train_t_u
val_t_un = 0.1 * val_t_u

我们的训练循环实际上并没有改变。我们只是想额外评估每个迭代周期的验证损失，以便有机会认识到我们是否过拟合：

# In[14]:
def training_loop(n_epochs, optimizer, params, train_t_u, val_t_u,
                  train_t_c, val_t_c):
    for epoch in range(1, n_epochs + 1):
        train_t_p = model(train_t_u, *params)    ⇽---  
        train_loss = loss_fn(train_t_p, train_t_c)

        val_t_p = model(val_t_u, *params)    ⇽---  除了train_*和val_*，这2行代码是相同的
        val_loss = loss_fn(val_t_p, val_t_c)

        optimizer.zero_grad()
        train_loss.backward()    ⇽---  注意，这里没有val_loss.backward()，因为我们不想在验证集上训练模型
        optimizer.step()

        if epoch <= 3 or epoch % 500 == 0:
           print(f"Epoch epoch, Training loss train_loss.item():.4f,"
                 f" Validation loss val_loss.item():.4f")

    return params

# In[15]:
params = torch.tensor([1.0, 0.0], requires_grad=True)
learning_rate = 1e-2
optimizer = optim.SGD([params], lr=learning_rate)

training_loop(
    n_epochs = 3000,
    optimizer = optimizer,
    params = params,
    train_t_u = train_t_un,    ⇽---  
    val_t_u = val_t_un,
    train_t_c = train_t_c,    ⇽---  由于我们再次使用SGD，我们又回到了使用归一化输入
    val_t_c = val_t_c)

# Out[15]:
Epoch 1, Training loss 66.5811, Validation loss 142.3890
Epoch 2, Training loss 38.8626, Validation loss 64.0434
Epoch 3, Training loss 33.3475, Validation loss 39.4590
Epoch 500, Training loss 7.1454, Validation loss 9.1252
Epoch 1000, Training loss 3.5940, Validation loss 5.3110
Epoch 1500, Training loss 3.0942, Validation loss 4.1611
Epoch 2000, Training loss 3.0238, Validation loss 3.7693
Epoch 2500, Training loss 3.0139, Validation loss 3.6279
Epoch 3000, Training loss 3.0125, Validation loss 3.5756

tensor([  5.1964, -16.7512], requires_grad=True)

在这里，我们对模型的处理并不是很公平。因为验证集很小，所以验证损失也只有在一定程度上才有意义。在任何情况下，我们注意到验证损失比训练损失要高，尽管不是一个数量级。我们期望模型在训练集上表现得更好，因为模型参数是由训练集塑造的。我们的主要目标是同时减少训练损失和验证损失。虽然在理想情况下，2种损失的值应大致相同，但只要验证损失与训练损失接近程度合理，我们就知道我们的模型在继续学习关于数据集的一般性知识。在图5.14中，C模型是理想的，D模型是可以接受的，而A模型根本不学习，B模型存在过拟合。我们将在第12章中看到更多关于过拟合的有意义的例子。

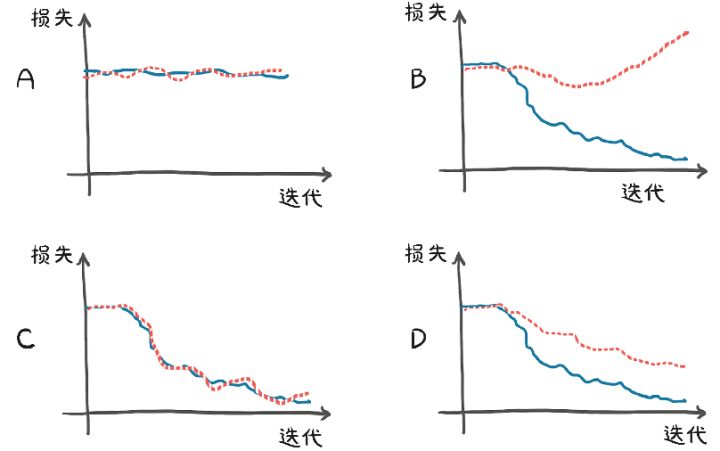
图5.14　在考虑训练（实线）和验证（虚线）损失时的过拟合场景。（A）由于数据中没有信息或模型没有足够的能力，导致训练损失和验证损失没有减少。（B）训练损失减少，而验证损失增加：过拟合。 （C）训练损失和验证损失同步减少，当模型不处于过拟合的极限时，性能可以进一步提高。 （D）训练损失和验证损失的绝对值不同，但趋势相似：过拟合得到控制

5.5.4　自动求导更新及关闭

从前面的训练循环中，我们可以了解到我们只对train_loss调用了backward()，因此，误差只会在训练集上反向传播。验证集用于提供一份独立的模型评估，评估模型对未用于训练的数据的输出的准确性。

好奇的读者此时会有一个小小的疑问，那就是对模型进行了2次评估，一次在train_t_u上，一次在val_t_u上，然后才调用backward()，这难道不会让自动求导“迷惑”吗？难道backward()不会受到在验证集上传递时生成的值的影响吗？

幸运的是，情况并非如此。训练循环中的第1行对train_t_u上的模型进行评估，以生成train_t_p，然后从train_t_p评估train_loss。这将创建一个计算图，将train_t_u、train_t_p和train_loss连接起来。当模型再次在val_t_u上求值时，将生成val_t_p和val_loss。在本例中，将创建一个单独的计算图，将val_t_u、val_t_p和val_loss连接起来。将单独的张量经过相同的函数，即model和loss_fn()运算，得到单独的计算图，如图5.15所示。

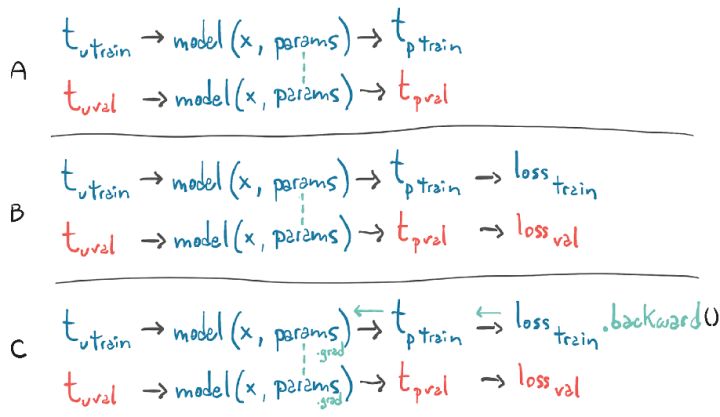
图5.15　通过一张图显示了对于2个损失，其中一个损失调用了backward()之后，梯度是如何传播的

图5.15中的A、B、C唯一相同的是张量的参数，当我们在train_loss上调用backward()时，我们在第1张图上运行backward()。换句话说，我们基于train_t_u生成的计算结果，将train_loss对参数的导数进行累加。

如果我们对val_loss误调用backward()，则会累加val_loss相对同一叶节点上的参数的导数。还记得zero_grad()吗？每次调用backward()时，梯度都是相互累加的，除非我们显式地将梯度归零。嗯，这里会发生一些非常相似的事情：在val_loss上调用backward()，在train_loss.backward()调用生成的结果之上，将导致梯度在params张量中累加。在这种情况下，我们将在整个数据集上（训练集和验证集）有效地训练我们的模型，因为梯度将依赖于这二者，非常有趣。

这里还有一个需要讨论的因素，既然我们从来没有在val_loss上调用backward()，那么为什么要首先构建这个图呢？实际上，我们可以只将model()和loss_fn()作为普通函数调用，而不用跟踪计算结果。无论如何优化，构建自动求导图都会带来额外的开销，在验证过程中我们完全可以放弃这些开销，特别是当模型有数百万个参数时。为了解决这个问题，PyTorch允许我们在不需要的时候关闭自动求导，使用上下文管理器torch.no_grad()[11]。在这个小问题上，我们并不会看到构建自动求导图在速度或内存开销方面有任何有意义的优势。不过，对于更大的模型，这些差异会累加起来。我们可以通过检查val_loss张量上的requires_grad属性的值来确保这是有效的：

# In[16]:
def training_loop(n_epochs, optimizer, params, train_t_u, val_t_u,
                  train_t_c, val_t_c):
    for epoch in range(1, n_epochs + 1):
        train_t_p = model(train_t_u, *params)
        train_loss = loss_fn(train_t_p, train_t_c)

        with torch.no_grad():    ⇽---  这里是上下文管理器
            val_t_p = model(val_t_u, *params)
            val_loss = loss_fn(val_t_p, val_t_c)
            assert val_loss.requires_grad == False    ⇽---  检查在此块中输出的requires_grad属性的值是否被强制设为False

        optimizer.zero_grad()
        train_loss.backward()
        optimizer.step()

使用相关的set_grad_enabled()，我们还可以根据一个布尔表达式设定代码运行时启用或禁用自动求导的条件，典型的条件是我们是在训练模式还是推理模式下运行。例如，我们可以定义一个calc_forward()方法，它接收数据作为输入，根据一个布尔类型的参数决定model()和loss_fn()是否会进行自动求导。

# In[17]:
def calc_forward(t_u, t_c, is_train):
    with torch.set_grad_enabled(is_train):
        t_p = model(t_u, *params)
        loss = loss_fn(t_p, t_c)
    return loss

本文摘自《PyTorch深度学习实战》

PyTorch核心开发者教你用PyTorch创建神经网络和深度学习系统的实践指南，基于Python3.6，提供源代码下载，PyTorch联合创作者作序推荐。

虽然很多深度学习工具都使用Python，但PyTorch 库是真正具备Python 风格的。对于任何了解NumPy 和scikit-learn 等工具的人来说，上手PyTorch 轻而易举。PyTorch 在不牺牲高级特性的情况下简化了深度学习，它非常适合构建快速模型，并且可以平稳地从个人应用扩展到企业级应用。由于像苹果、Facebook和摩根大通这样的公司都使用PyTorch，所以当你掌握了PyTorth，就会拥有更多的职业选择。
本书是教你使用 PyTorch 创建神经网络和深度学习系统的实用指南。它帮助读者快速从零开始构建一个真实示例：肿瘤图像分类器。在此过程中，它涵盖了整个深度学习管道的关键实践，包括 PyTorch张量 API、用 Python 加载数据、监控训练以及将结果进行可视化展示。

本书主要内容：
（1）训练深层神经网络；
（2）实现模块和损失函数；
（3）使用 PyTorch Hub 预先训练的模型；
（4）探索在 Jupyter Notebooks 中编写示例代码。

本书适用于对深度学习感兴趣的 Python 程序员。了解深度学习的基础知识对阅读本书有一定的帮助，但读者无须具有使用 PyTorch 或其他深度学习框架的经验。