论文笔记：NAOMI: Non-Autoregressive MultiresolutionSequence Imputation

Posted 2022-05-04 UQI-LIUWJ

2019 NIPS

0 abstract

缺失值插补是时空建模中的一个基本问题，从运动跟踪到物理系统的动力学。深度自回归模型受到错误传播的影响，这对于输入远程序列来说是灾难性的。在本文中，我们采用非自回归方法并提出了一种新颖的深度生成模型：非自回归多分辨率插补 (NAOMI)，用于在给定任意缺失模式的情况下插补远程序列。 NAOMI 利用时空数据的多分辨率结构，并使用分而治之的策略从粗粒度到细粒度分辨率递归解码。我们通过对抗训练进一步增强了我们的模型。当对来自确定性和随机动力学系统的基准数据集进行广泛评估。在我们的实验中，NAOMI 展示了插补精度的显着提高（与自回归对应物相比，平均误差减少了 60%）和远程序列的泛化。

1 introduction

缺失值的问题经常出现在现实生活中的序列数据中。 例如，在运动跟踪中，由于物体遮挡、轨迹交叉和相机运动的不稳定性，轨迹通常会包含缺失数据[1]。 缺失值会在训练数据中引入观察偏差，使学习变得不稳定。 因此，输入缺失值对于下游序列学习任务至关重要。 序列插补在统计学文献中已经研究了几十年 [2, 3, 4, 5]。 大多数统计技术都依赖于对缺失模式的强假设，例如随机缺失，并且不能很好地推广到看不见的数据。 此外，现有方法在缺失数据比例高、序列长的情况下效果不佳。

最近的研究 [6, 7, 8, 9] 提出使用深度生成模型从序列数据中学习灵活的缺失模式。 然而，所有现有的深度生成插补方法都是自回归的：它们使用来自先前时间步长的值对当前时间戳的值进行建模，并以顺序方式插补缺失数据。 因此，自回归模型非常容易受到复合误差的影响，这对于远程序列建模来说可能是灾难性的。 我们在实验中观察到，现有的自回归方法在具有长程动力学的序列插补任务上存在困难。

在本文中，我们介绍了一种用于远程序列插补的新型非自回归方法。 我们不是仅以先前的值为条件，而是对历史和（预测的）未来的条件分布进行建模。 我们利用时空序列的多分辨率特性，并将复杂的依赖关系分解为多个分辨率的简单依赖关系。 我们的模型，非自回归多分辨率插补 (NAOMI)，采用分而治之的策略来递归地填充缺失值。 我们的方法是通用的，可以用于各种学习目标。 我们将模型的实现作为开源项目发布。

总之，我们的贡献如下：

• 我们为深度生成模型提出了一种新颖的非自回归解码程序，该程序可以为具有长期依赖关系的时空序列估算缺失值。

• 我们使用生成对抗模仿学习目标和完全可微的生成器来引入对抗训练，以减少方差。

• 我们对基准序列数据集进行了详尽的实验，包括交通时间序列、台球和篮球轨迹。 我们的方法展示了 60% 的准确性提高，并在给定任意缺失模式的情况下生成逼真的序列。

 

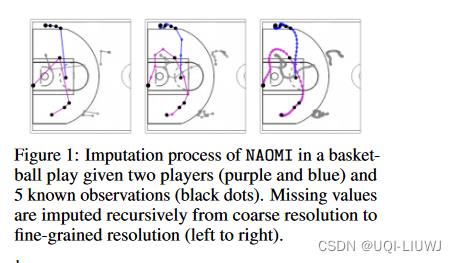
2 related work

2.1 missing value imputation

现有的缺失值插补方法大致分为两类：统计方法和深度生成模型。

统计方法通常对缺失模式强加强假设。 例如，均值/中值平均 [4]、线性回归 [2]、MICE [10] 和 k 近邻 [11] 只能处理随机丢失的数据。 使用 EM 算法 [12] 的潜变量模型可以估算数据丢失不是随机的，但是仅限于某些参数模型。

深度生成模型提供了一个灵活的缺失数据插补框架。 例如，[13,6,14] 开发了循环神经网络的变体来估算时间序列。 [8, 9, 7] 利用生成对抗训练 (GAN) [15] 来学习复杂的缺失模式。 然而，所有现有的插补模型都是自回归的。

2.2 non-autoregressive modeling

在自然语言处理 [16, 17, 18] 和语音 [19] 中，非自回归模型已经获得了比自回归模型的竞争优势。 例如，[19] 使用归一化流模型 [20] 来训练用于语音合成的并行前馈网络。 对于神经机器翻译，[16] 引入了具有一系列离散潜在变量的潜在生育力模型。 同样，[17, 18] 提出了一个完全确定的模型来减少监督量。 所有这些工作都突出了非自回归模型在以可扩展方式解码序列数据方面的优势。 我们的工作是第一个具有新颖递归解码算法的序列插补任务的非自回归模型。

2.3 GAN

生成对抗网络 (GAN) [15] 引入了一个鉴别器来代替最大似然目标，这引发了生成建模的新范式。 对于序列数据，对整个序列使用鉴别器会忽略序列依赖性，并且可能会遭受模式崩溃。 [21, 22] 开发模仿和强化学习以在顺序设置中训练 GAN。 [21]提出了将GAN和逆强化学习结合起来的生成对抗模仿学习。 [22] 使用强化学习为离散序列开发 GAN。 我们使用具有可微分策略的模仿学习公式。

2.4 多分辨率生成

我们的方法与图像的多分辨率生成模型具有相似性，例如 Progressive GAN [23] 和多尺度自回归密度估计 [24]。 关键区别在于 [23, 24] 仅捕获空间多分辨率结构并假设不同分辨率的加法模型。 我们处理多分辨率时空结构并递归生成预测。 我们的方法与分层序列模型 [25,26,27] 根本不同，因为它只跟踪最相关的隐藏状态并即时更新它们，这具有内存效率且训练速度更快。

3 Non-Autoregressive Multiresolution Sequence Imputation

令 X = (x1, x2, ..., xT ) 是 T 个观测的序列，其中每个时间步长。 X 有缺失数据，由掩码序列 M = (m1, m2, ..., mT ) 指示。 每当 xt 缺失时，相应的掩蔽 mt 为零。 我们的目标是用一组序列的合理值替换缺失的数据。

缺失值插补的一种常见做法是直接对不完整序列的分布进行建模。 可以使用链式法则分解概率 并训练一个（深度）自回归模型用于插补 [6, 7, 8, 9]。

然而，自回归模型的一个关键弱点是它们的顺序解码过程。 由于当前值取决于先前的时间步长，因此自回归模型通常不得不求助于次优束搜索，并且容易受到远程序列的误差复合影响 [16,17,18]。

这种弱点在序列插补中更加严重，因为模型无法基于已知的未来，这导致插补值与实际观测值不匹配。 为了缓解这些问题，我们改为采用非自回归方法并提出一种深度、非自回归、多分辨率生成模型 NAOMI。 

 3.1 NAMOI 结构

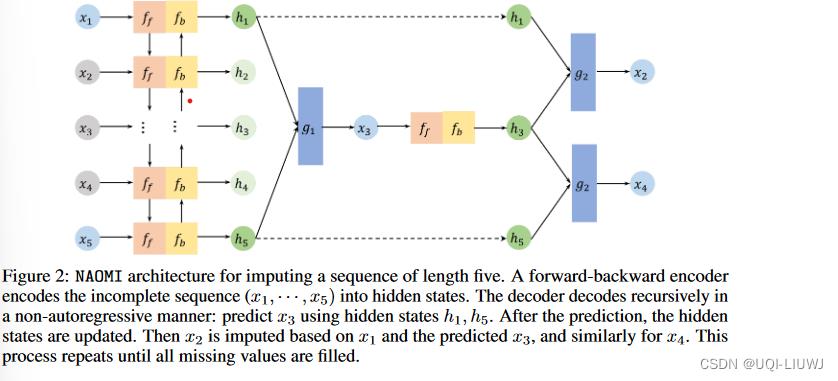
如图 2 所示，NAOMI 有两个组件：

1）将不完整序列映射到隐藏表示的前向后向编码器

 2）在给定隐藏表示的情况下估算缺失值的多分辨率解码器

 3.1.1 forward-backward encoder

 我们将观测序列和mask序列拼接，于是有I=[X,M]

我们的编码器对给定输入的两组隐藏状态的条件分布进行建模

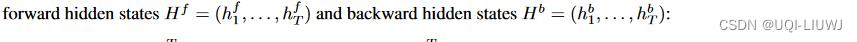
 我们将前向和后向条件分布用前向RNN 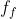和后向RNN 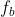表示

 

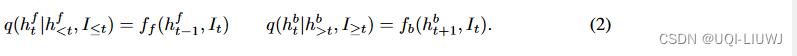
 3.1.2 multiresolution decoder

给定联合hidden state 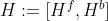,decoder 学习完整序列的分布 p(X|H)

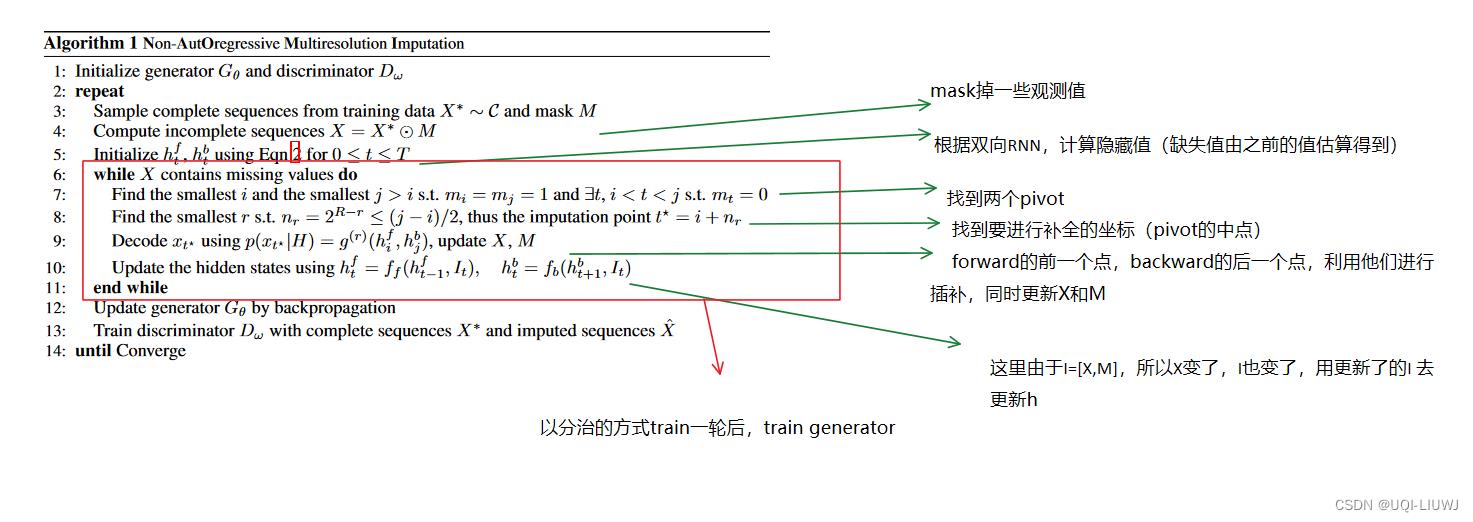
我们采用分而治之的策略，从粗粒度到细粒度分辨率递归解码。 如图 2 所示，在每次迭代中，解码器首先将两个已知时间步标识为枢轴（本例中为 x1 和 x5），并在其中点 (x3) 附近进行估算。 然后用新估算的步骤替换一个枢轴，并以更精细的分辨率对 x2 和 x4 重复该过程。

如果动态是确定性的，则 g(r) 直接输出估算值。

对于随机动力学，g(r) 输出各向同性高斯分布的均值和标准差，并使用重新参数化技巧从高斯分布中采样预测 [28]。

插补后掩码 mt 更新为 1，并且该过程进行到下一个分辨率。 这个解码过程的细节在算法 1 中描述。

3.1.3 高效的隐藏状态更新

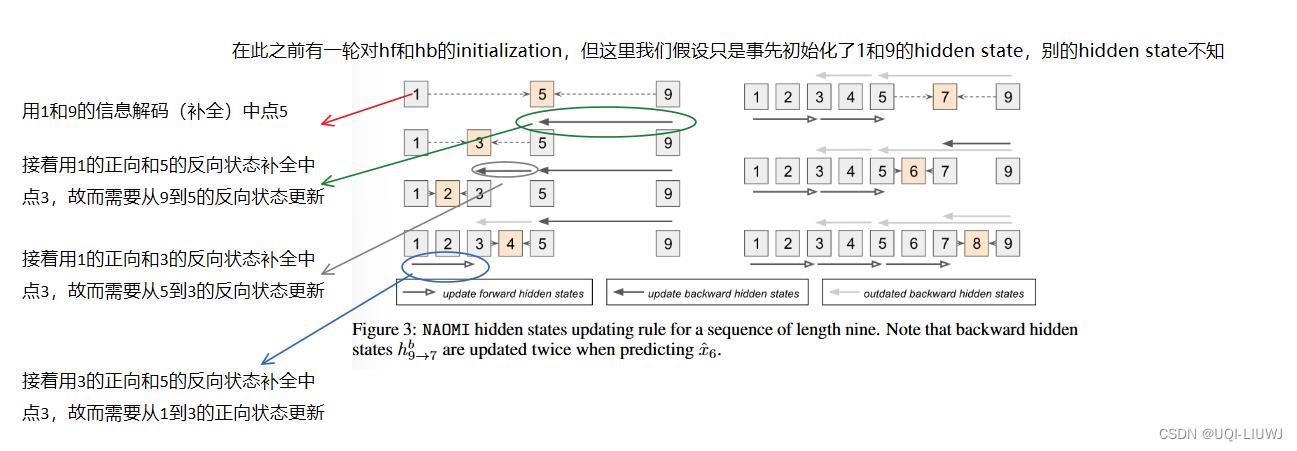
NAOMI 通过重用之前的计算来有效地更新隐藏状态，这与自回归模型具有相同的时间复杂度。 图 3 显示了一个长度为 9 的序列的示例。

• 灰色块是已知的时间步长。
• 橙色块是要估算的目标时间步长。
• 空心箭头表示前向隐藏状态更新
• 黑色箭头表示后向隐藏状态更新。
• 灰色箭头是过时的隐藏状态更新。
• 虚线箭头表示解码步骤。

较早的隐藏状态存储在估算的时间步中并被重用。 因此，前向隐藏状态 hf 只需更新一次，后向隐藏状态 hb 最多更新两次。

 

 3.2 学习目标

令是完整序列的集合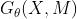，表示以θ作为参数的NAOMI生成模型（补全），p(M)表示masking的先验。于是补全模型可以用如下的目标函数进行训练：

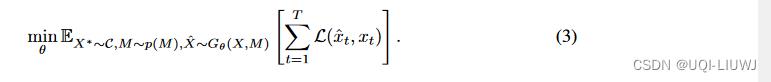
         其中L是某种损失函数，对于确定型动力学，我们使用MSE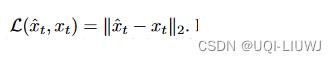

        对于随机动力学，我们可以用鉴别器替换 L，这会导致对抗性训练目标。 我们使用与生成对抗模仿学习 (GAIL) [21] 类似的公式，它在序列级别量化生成数据和训练数据之间的分布差异。 

 

3.2.1 对抗学习

给定NAOMI中的生成器Gθ，以及鉴别器Dω，对抗学习的目标函数是：

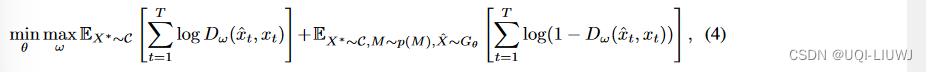
GAIL 直接从生成器中对序列进行采样，并使用策略梯度优化参数。 这种方法可能会受到高方差的影响，并且需要大量样本[29]。 我们不是采样，而是采用基于模型的方法并使我们的生成器完全可微。 我们通过将隐藏状态映射到高斯分布的均值和方差，在每个时间步应用重新参数化技巧 [28]。 

4 实验

我们在具有不同动态的环境中评估 NAOMI：真实世界的交通时间序列、来自物理引擎的台球轨迹以及来自职业篮球比赛的团队运动。

我们与以下基线进行比较：

• 线性：线性插值，缺失值是使用来自两个最接近的已知观测值的插值预测来估算的。

• KNN[11]：k 个最近邻，缺失值被估算为k 个最近邻序列的平均值。

• GRUI [9]：使用GAN 进行时间序列插补的自回归模型，经过修改以处理完整的训练序列。判别器对整个时间序列应用一次。

• MaskGAN[7]：具有actor-critic GAN的自回归模型，使用对抗性模仿学习进行训练，每个时间步都应用判别器，仅使用前向编码器，并以单一分辨率解码。

• SingleRes：我们模型的自回归对应版本，使用对抗性模仿学习进行训练，使用前向后向编码器，但以单一分辨率解码。如果没有对抗性训练，它会简化为 BRITS [14]。

我们随机选择要掩蔽的步数，然后在序列中随机抽取要掩蔽的具体步数。因此，模型在训练期间学习了各种缺失模式。我们对所有方法使用相同的掩码方案，包括 MaskGAN 和 GRUI。有关实施和培训的详细信息，请参见附录。

4.1 补全交通数据

PEMS-SF 交通时间序列 [30] 数据包含 267 个训练序列和 173 个测试序列，长度为 144（全天每 10 分钟采样一次）【个人猜测每天一个测试序列，每一个序列144*963 维】。 它是具有 963 个维度的多元变量，代表从 963 个不同传感器收集的高速公路占用率。 我们为每个具有 122 到 140 个缺失值的数据生成一个掩码序列。

4.1.2 补全准确率

估算的缺失值与其真实值之间的 L2 损失最准确地衡量了生成序列的质量。 如表 1 所示，NAOMI 大大优于其他方法，与自回归基线相比，L2 损失减少了 23%。 KNN 表现相当不错，主要是因为训练数据中重复的每日流量模式。 简单地在训练数据中找到一个相似的序列就足以进行插补。

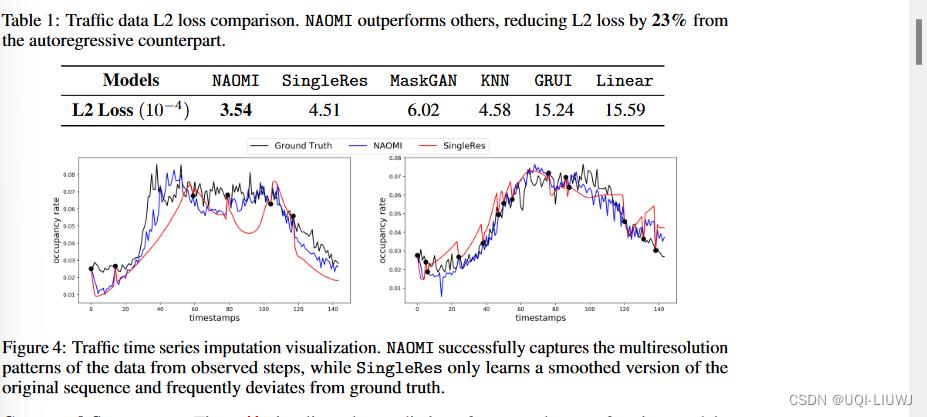
 4.1.3 生成的序列

图 4 可视化了来自两个性能最佳模型的预测：NAOMI（蓝色）和 SingleRes（红色）。 黑点是观察到的时间步长，黑色曲线是ground truth。 NAOMI 成功地捕捉到了 ground truth 时间序列的模式，而 SingleRes 失败了。 NAOMI 学习植根于基本事实的多尺度波动，而 SingleRes 只学习一些平均行为。 这证明了使用多分辨率建模的明显优势。

4.2 补全台球轨迹

我们使用 [31] 中的模拟器在矩形世界中生成 4000 个训练和 1000 个台球轨迹测试序列。 每个球都使用随机位置和随机速度进行初始化，并滚动 200 个时间步长。（每个序列200*2维） 所有的球都有固定的尺寸和均匀的密度，并且没有摩擦。 我们为每个轨迹生成一个掩蔽序列，其中包含 180 到 195 个缺失值。

4.2.1 补全准确

在这种情况下，物理学的三个决定性特征是：（1）直线运动； (2) 保持不变的速度； (3) 撞墙反射。

因此，我们采用四个指标来量化所学物理：（1）估算值和真实值之间的 L2 损失； (2) 测量生成轨迹直线度的弯曲度； (3)平均步长变化来衡量球的速度变化； (4) 反射点与墙壁的距离，检查模型是否学习了物理底层碰撞和反射。

 

所有模型的比较 （记为“这些指标”）。如表 2 所示。“专家”表示来自模拟器的真实轨迹。 更接近“专家”的统计数据更好。 我们观察到 NAOMI 在几乎所有指标中的整体性能最好，其次是 SingleRes 基线。

可以 预计到的是，线性将执行最佳的单步变化。 根据设计，线性插值保持最接近真实情况的恒定步长变化。

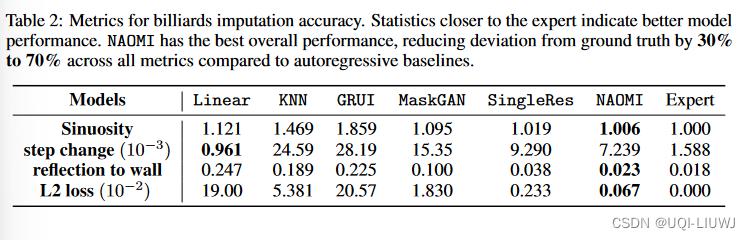
4.2.2 生成的轨迹

我们将图 5 中的估算轨迹可视化。有 8 个已知时间步长（黑点），包括起始位置。 NAOMI 可以成功恢复原始轨迹，而 SingleRes 明显偏离。 值得注意的是，在一开始，SingleRes 错误地预测球会从上墙而不是左墙反弹。 因此，SingleRes 必须纠正其行为以匹配后续的观察结果，从而导致弯曲和不切实际的轨迹。 在左下角附近可以看到另一个偏差，NAOMI 产生的轨迹路径在两次从墙上反弹后真正平行，但 SingleRes 没有。 

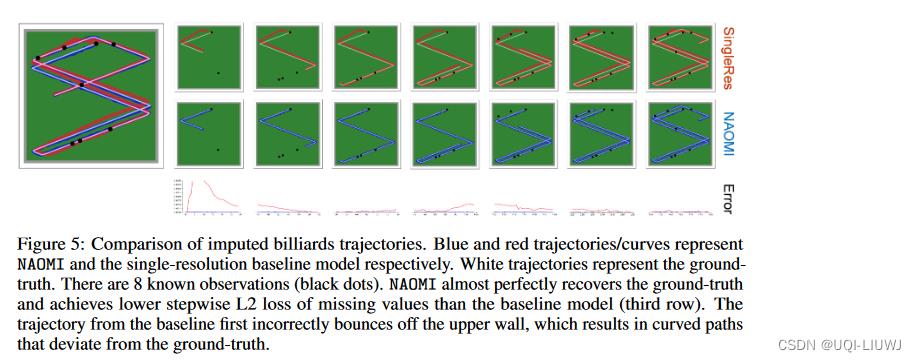
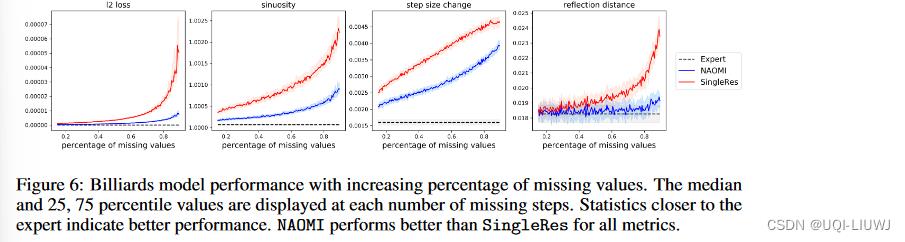
4.2.3 对于丢失比例的鲁棒性

图 6 比较了 NAOMI 和 SingleRes 在我们增加缺失值比例时的性能。 显示每个指标的中值和 25、75 个百分位值。 由于动态是确定性的，更高的缺失部分通常意味着更大的差距，从而更难找到正确的解决方案。 当我们增加缺失值的百分比时，我们可以看到两个模型的性能都急剧下降，但 NAOMI 在所有指标上仍然优于 SingleRes。

 4.3 补全篮球运动员移动

篮球跟踪数据集包含职业篮球运动员的进攻轨迹，有 107,146 个训练序列和 13,845 个测试序列。 每个序列包含 5 名球员的 (x, y) 坐标，以 6.25Hz 进行 50 个时间步长，并发生在左半场。 我们为每个轨迹生成一个掩蔽序列，其中包含 40 到 49 个缺失值。

4.3.1 补全的准确性 

 由于环境是随机的（进攻的篮球运动员的目标是不可预测的），测量我们的模型输出和ground-truth之间的 L2 损失不一定是现实轨迹的良好指标 [32, 33]。

因此，我们遵循以前的工作并计算特定领域的指标来比较轨迹质量：（1）平均轨迹长度来测量 8 秒内的典型球员运动； (2) 平均出界率，衡量轨迹出界的几率； (3) 平均步长变化来量化玩家运动变化； (4) 最大-最小路径差异； (5) 代表团队协调性的平均球员距离。

表 3 比较了使用这些指标的模型性能。 “专家”代表真实的情况，越接近“专家”数据越好。 NAOMI 在几乎所有指标上都优于基线。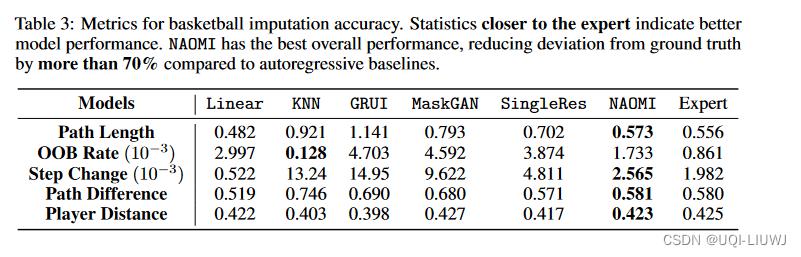

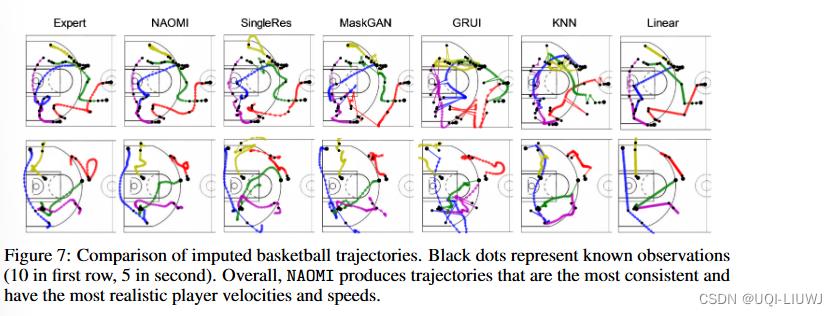
4.3.2 生成轨迹

我们将图 7 中所有模型的估算轨迹可视化。NAOMI 生成的轨迹与已知观察结果最一致，并且具有最真实的运动员速度。 相比之下，其他基线模型在这些方面经常失败。

KNN 会生成具有不自然跳跃的轨迹，因为通过密集的已知观测值很难找到最近的邻居。

当已知的观测值很少时，线性无法生成曲线轨迹。

GRUI 生成与已知观测不一致的轨迹。 这主要是由于将鉴别器应用于整个序列而导致的模式崩溃。

MaskGAN 依赖于 seq2seq 和单个编码器，无法以未来的观察为条件并预测直线。

 4.3.3 对丢失比例的鲁棒性

图 8 比较了 NAOMI 和 SingleRes 在我们增加缺失值比例时的性能。 显示每个指标的中值和 25、75 个百分位值。 请注意，我们总是观察第一步。 一般来说，缺失值越多，插补就越困难，也给模型预测带来更多的不确定性。 我们可以看到两个模型的性能（平均性能和插补方差）随着缺失值的增加而下降。 但是，在缺失值达到一定百分比时，两种模型的插补性能都开始提高。

这显示了可用信息与插补中生成模型的约束数量之间的有趣权衡。 更多的观察提供了有关数据分布的更多信息，但也可以限制学习模型的输出。 随着我们减少观察次数，该模型可以学习更灵活的生成分布，而不符合观察到的时间步长施加的约束。

5 结论

我们提出了一种深度生成模型 NAOMI，用于在远程时空序列中输入缺失数据。 NAOMI 使用非自回归方法递归地查找和预测从粗粒度到细粒度分辨率的缺失值。 利用多分辨率建模和对抗训练，NAOMI 能够在已知很少的观察值的情况下学习条件分布。 未来的工作将研究如何在无法获得完整的训练序列时推断潜在分布。 部分观察和外部约束之间的权衡是深度生成插补模型的另一个方向。