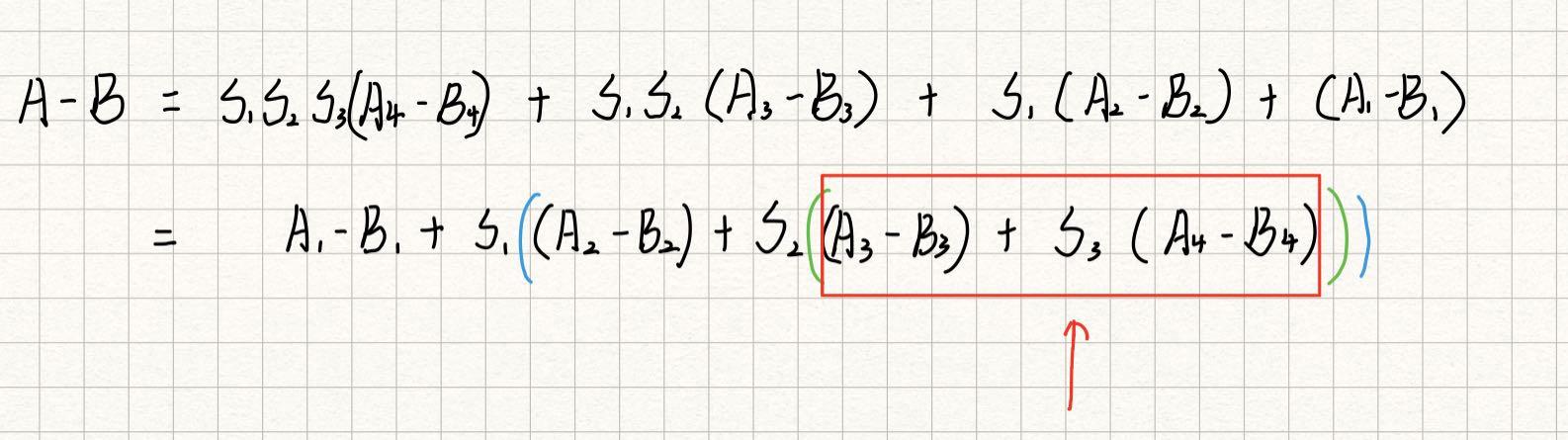蓝桥杯第十三届蓝桥杯真题 AK 攻略 —— C++ B组全真题超详细剖析

Posted 2022-05-04 秋刀鱼与猫_

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了蓝桥杯第十三届蓝桥杯真题 AK 攻略 —— C++ B组全真题超详细剖析相关的知识，希望对你有一定的参考价值。

🎄目录

🌼写在前面
💗写在最后

🌼写在前面

Hello朋友们😋，我是秋刀鱼🐟，一只活跃于Java区与算法区的新人博主~

欢迎大家加入高校算法学习社区🏰，社区里大佬云集，大家互相交流学习！

蓝桥杯的成绩已经公布，看到很多朋友拿了奖秋刀鱼很是高兴！大家都是好样的！因为疫情缘故秋刀鱼的蓝桥杯比赛被推迟到了 5 月 14 日第二批，因此还有半个月的时间进行准备。今天呢给大家带来蓝桥杯 C++ B组真题解析，这套题目也是耗费了我将近 7 个小时的时间才AK，希望看完能让你有所收获。如果觉得博主写的还不错的话务必三连支持一下：

🎉🎉主页：秋刀鱼与猫🎉🎉 🎉🎉期待你的支持与关注~🎉🎉

🌻 A题 — 九进制转十进制

🌷 题目描述

🌷 解题思路

很简单一道进制转换题目！这可不能做错哦！

🌷 代码编写

#include <iostream>
#include <cmath> 
using namespace std;

int main() 
	cout << 2 * pow(9, 0) + 2 * pow(9, 1) + 0 * pow(9, 2) + 2 * pow(9, 3) << endl;
	return 0;

🌻 B题 — 顺子日期

🌷 题目描述

🌷 解题思路

这道题实现起来还算简单，但是题目中的说明有点模棱两可，012到底能不能作为顺子呢？最后官方说明两个答案都算正确。

🌷 代码编写

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int months[] = 
 0, 31, 28, 31, 30, 31,
 30, 31, 31, 30, 31, 30,
 31
;

bool check(string str)

 for (int i = 0; i + 2 < str.size(); i ++ )
     if (str[i + 1] == str[i] + 1 && str[i + 2] == str[i] + 2)
         return true;

 return false;


int main()

 int year = 2022, month = 1, day = 1;
 int res = 0;
 for (int i = 0; i < 365; i ++ )
 
     char str[10];
     sprintf(str, "%04d%02d%02d", year, month, day);
     if (check(str))
     
         res ++ ;
         cout << str << endl;
     
     if ( ++ day > months[month])
     
         day = 1;
         month ++ ;
     
 
 cout << res << endl;
 return 0;

🌻 C题 — 刷题统计

🌷 题目描述

题传送门

🌷 解题思路

计算出从周一开始刷题一周的刷题数量 $w e e k C o s t$ ，将 $n / w e e k C o s t$ 获取到需要多少个周，更新答案。获取剩余的题目，剩余的题目一定能在一周之内完成，继续枚举获取答案值。非常简单！

🌷 代码编写

#include <iostream>
#define ll long long
using namespace std;

int main() 
	ll a, b, n;
	cin >> a >> b >> n;
	ll weekCost = a * 5 + b * 2;
	ll ans = 0;
	ans += (n / weekCost) * 7;
	n %= weekCost;
	for (int i = 1; n > 0 && i <= 7; ++i,++ans) 
		if (i <= 5) 
			n -= a;
		
		else 
			n -= b;
		
	
	cout << ans;
	return 0;

🌻 D题：修剪灌木

🌷 题目描述

题目传送门

🌷 解题思路

解决本题的关键是判断每棵灌木最高的高度，简单地思考不难发现该高度与该点距离左、右侧边界的距离相关。定义左侧边界距离为 $i$ ，则右侧边界可计算出为： $n - i - 1$ ，如下图所示：

灌木的最高高度就是： $max\\i,n-i-1\\ * 2$

🌷 代码编写

#include <iostream>
#include <math.h>
#define ll long long
using namespace std;
int main() 
	int n;
	cin >> n;
	for (int i = 0; i < n; ++i) 
		cout << max(i , (n - i - 1)) * 2;
		cout << endl;
	
	return 0;

🌻 E题：X进制减法

🌷 题目描述

题目传送门

🌷 解题思路

理解题意

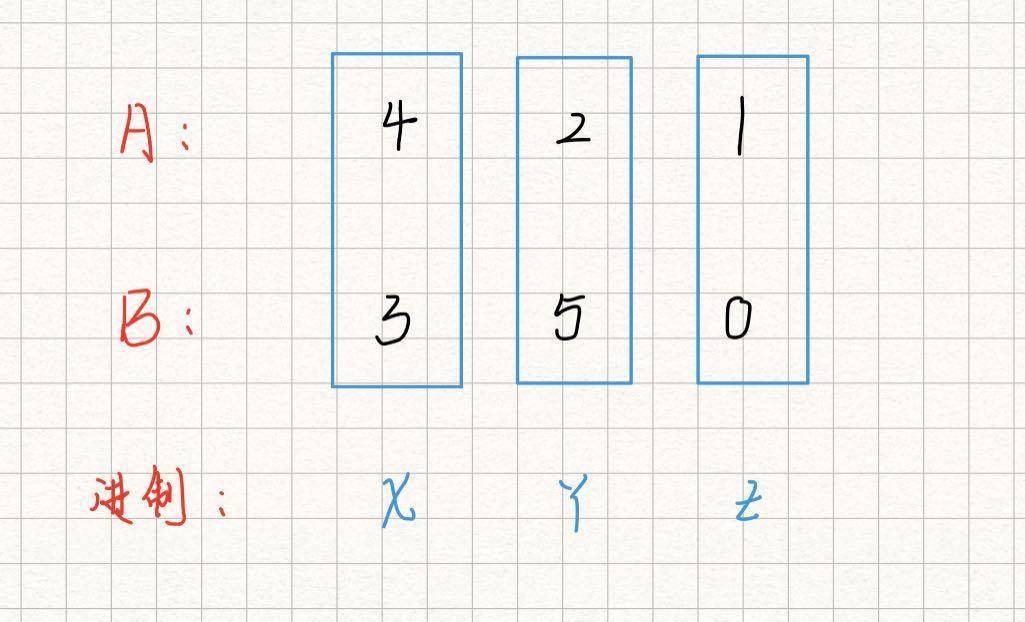
我相信很多朋友不会做这道题是因为题目的意思没有理清楚。其实题目的要求很简单：给定了两个整数 A,B，这两个数每一位上可以是任意进制，但是A，B相同位上进制规则相同。举个栗子：

若 X，Y，Z 分别代表 5,6,2 进制，则 A = 4*6*2 + 2*6 + 1 ,B = 3*6*2 + 5*6 + 0

如 X，Y，Z 分别代表 6,7,3 进制，则 A = 4*7*3 + 2*7 + 1 ,B = 3*7*3 + 5*7 + 0

无论每一位进制为何值，都需要满足：

进制数要大于改位的最大值
进制数的最小值为 2

满足上述要求的每一位进制所得到的数：A，B ，题目要求获取 A - B 的最小值。

解题方法

首先给出结论：只需要将每一位进制数设置为最小值， A - B 的值一定是最小值。

结论证明

首先假设 A 的每一位值为 $A_i$ ，最低位的值为 $A_1$ ，最高位的值为 $A_n$ ，B 同理。同时假设每一位的进制为 $S_i$ 最低位进制为 $S_1$ ，最高位进制为 $S_n$ 。下面以 n = 4 为例进行证明：

经过推导不难发现 A-B 的值能进行如下的表示：

先考虑箭头所指位置：题目中给定了 $A - B > 0$ ，因此 $A_4 - B_4 >= 0$ 恒成立，为了使结果值最小，因此 $S_3$ 的值应当最小。

继续看箭头所指的位置，因为 $S_3$ 是第三位的进制数，因此 $S_3 > A_3$ 且 $S_3 > B3$ ，而 $A_4 - B_4 >=0$ ，因此 $S_3(A_4-B_4) >= (A_3-B_3)$ ，因此方框位置的值仍为正数或 0 ，为了使该值最小， $S_2$ 应当取最小值。

继续证明的思路与上述思路相同，通过证明最终得出：为了使 $A - B$ 的值最小，每一位的表示的进制数应当最小！

🌷 代码编写

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int mod = 1000000007;
int main() 
	int N, ma, mb;
	int nums[100001];
	ll ans = 0;
	memset(nums, 0, sizeof nums);
	cin >> N;
	cin >> ma;
	for (int i = 0; i < ma; ++i) 
		cin >> nums[i];
	
	cin >> mb;
	for (int i = 0; i < ma; ++i) 
		int val = 0;
		if (mb + i >= ma) 
			cin >> val;
		
        // 必须满足进制数大于 2 这个前提
		ans *= max(max(nums[i], val) + 1, 2);
		ans += (nums[i] - (ll)val);
		ans %= mod;
	
	cout << ans;
	return 0;

🌻 F题：统计子矩阵

🌷 题目描述

题目传送门

【评测用例规模与约定】

对于 30% 的数据，N, M ≤ 20.

对于 70% 的数据，N, M ≤ 100.

对于 100% 的数据，1 ≤ N, M ≤ 500; 0 ≤ *Ai j* ≤ 1000; 1 ≤ K ≤ 250000000**

🌷 解题思路

二维前缀和

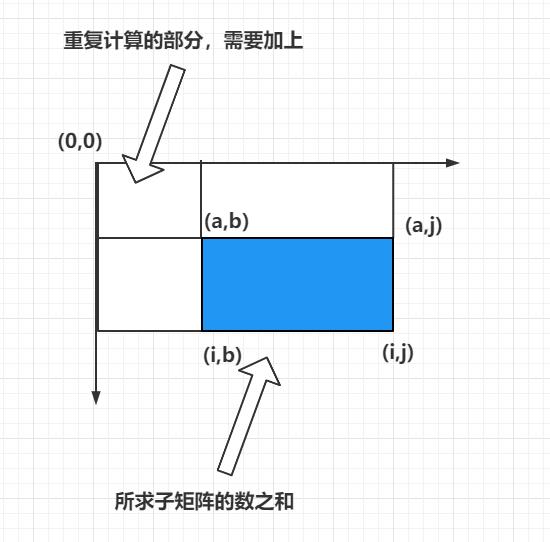
对于任意一个矩阵，如何快速获取到任意一个字矩阵中所有数的和呢？可以使用二维前缀和的思想。定义一个二维前缀和数组 $s u m [n] [m]$ 记录前缀和， $s u m [i] [j]$ 记录 $(0, 0) - > (i, j)$ 矩阵中的数之和，就如下图所示：

获取任意一个子矩阵 $(a, b) - > (i, j)$ 矩阵数之和等于： $s u m [i] [j] - s u m [a - 1] [j] - s u m [i] [b - 1] + s u m [a - 1] [b - 1]$ 如下图所示：

只需要预先处理好前缀和数组，按照上述方式就能够在
以上是关于蓝桥杯第十三届蓝桥杯真题 AK 攻略 —— C++ B组全真题超详细剖析的主要内容，如果未能解决你的问题，请参考以下文章

蓝桥杯国赛真题21Scratch水果拼图第十三届蓝桥杯图形化编程scratch国赛真题和答案讲解

蓝桥杯国赛真题22Scratch镜像画笔第十三届蓝桥杯图形化编程scratch国赛真题和答案讲解

蓝桥杯国赛真题24Scratch货物运输第十三届蓝桥杯图形化编程scratch国赛真题和答案讲解

蓝桥杯国赛真题25Scratch数字与图形第十三届蓝桥杯图形化编程scratch国赛真题和答案讲解

蓝桥杯国赛真题23Scratch恐龙跑酷第十三届蓝桥杯图形化编程scratch国赛真题和答案讲解

蓝桥杯国赛真题23Scratch恐龙跑酷第十三届蓝桥杯图形化编程scratch国赛真题和答案讲解

蓝桥杯第十三届蓝桥杯真题 AK 攻略 —— C++ B组全真题超详细剖析

🎄目录

🌼写在前面

🌻 A题 — 九进制转十进制

🌷 题目描述

🌷 解题思路

🌷 代码编写

🌻 B题 — 顺子日期

🌷 题目描述

🌷 解题思路

🌷 代码编写

🌻 C题 — 刷题统计

🌷 题目描述

🌷 解题思路

🌷 代码编写

🌻 D题： 修剪灌木

🌷 题目描述

🌷 解题思路

🌷 代码编写

🌻 E题：X进制减法

🌷 题目描述

🌷 解题思路

🌷 代码编写

🌻 F题：统计子矩阵

🌷 题目描述

🌷 解题思路

🌻 D题：修剪灌木