DirectX 9.0读书笔记 向量
Posted i_dovelemon
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了DirectX 9.0读书笔记 向量相关的知识,希望对你有一定的参考价值。
引言
在游戏开发中,向量(Vector)的应用无处不在,诸如碰撞检测,物理仿真,计算机3D图形学中,都可以看到向量的身影。所以,想要学好3D图形学,或者物理仿真之类的技术,向量是必须要掌握的基本功。
在下面将简单介绍一些向量的基本使用方法。
向量的定义
向量指的是同时具有长度和方向的一个量。这样的具有长度和方向的量被称为矢量,而只有长度,没有方向的量被称为标量。所以向量是矢量的一种。在物理上,矢量到处可见,如力,位移,速度等都是矢量,他们有方向,有大小。
向量的表示
在图形上,向量使用一个带箭头的线段来表示。
在数值上,向量用坐标系中的坐标来表示。从这个坐标系的原点,到向量的坐标的一条带箭头的线段,就是向量的图形表示了。
在表达式中,向量使用下图的方式表示:
 即表达式的字符,上面带有一个箭头,这整个符号就表示一个向量。
即表达式的字符,上面带有一个箭头,这整个符号就表示一个向量。
左手坐标系和右手坐标系
在DirectX中使用的是称为左手坐标系的3D坐标系。左手坐标系的判定方法如下:
如果你将你的左手手指指向正X轴,然后自然弯曲,弯曲的方向是朝着正Y轴方向弯曲,将大拇指伸直。如果大拇指指向的方向为正Z轴的话,那么这个坐标系就是左手坐标系。
如果读者看文字,不太清楚的话,可以看下图,图中不仅给出了左手坐标系,还给出了右手坐标系的判定方法:
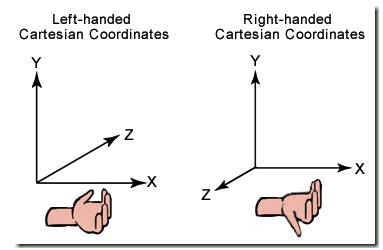
(Left-handed Cartesian Coordinate 为左手坐标系,即左边的图, Right-handed Cartesian Coordinate为右手坐标系,即右边的图)
向量基本操作及几何意义
在上面我们说过,向量可以使用数值方式来表示,也就是说,可以用下面的方式来表示一个向量:

那么对于这样的数值方式,我们可以进行什么样的操作了?(注意这里讨论的都是3D向量了)
向量加法:
向量加法指的是将两个向量进行相加,他们的计算方式是将向量的各个分量进行相加, 如下所示:
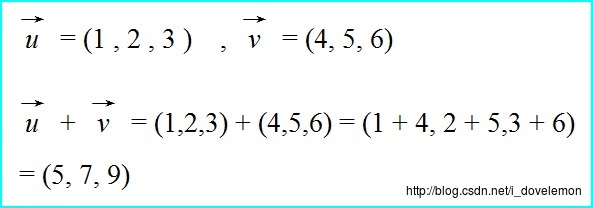
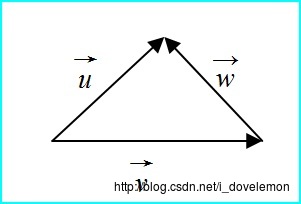
在几何图形上,向量加法指的是如下的概念:
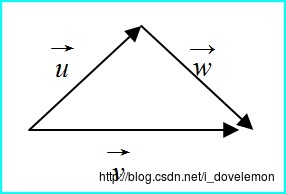
向量减法:
同加法一样,只是将各个分量进行相减而已,如下所示:
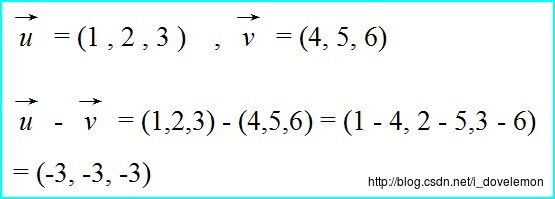
在几何图形上,向量减法是如下的意思:
向量标量乘法:
标量乘法,指的是用一个标量乘以一个向量(标量指的是只有大小,没有方向的数值),如下图所示:

由于向量的标量除法,就是将k值变为1/k,然后与向量进行向量乘法,这里不再赘述。
他们的几何意义如下图所示:

向量长度:
向量是有长度的,那么向量的长度如何计算了,通过下面的表达式我们就可以计算出向量的长度:
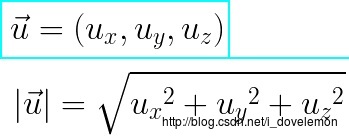
单位向量:
长度为1的向量,我们称之为单位向量,将一个非单位向量的向量,转变为单位向量的过程,我们称之为归一化(normalize)
进行归一化的操作公式如下所示:

向量点积(Dot):
向量点积,是在向量上定义的一种运算,通过将两个向量进行点积运算,我们可以得到一个标量。它的定义公式如下:
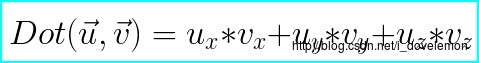
进行点积的几何意义看上去不是那么的明显,但是,我们可以通过cos函数,来解释它的几何意义:

如果当u和v都是单位向量的时候,将他们进行点积运算,得到的就是他们之间夹角的余弦cos,所以通过上面的点积算法,我们可以得到任意两个向量之间的夹角。
向量叉积(Cross):
向量叉积是用来计算垂直于进行叉积运算的两个向量的向量,所以这个运算是3D向量独有的,在2D向量中,不存在同时垂直于两个不平行的向量的向量。它的数学定义如下:
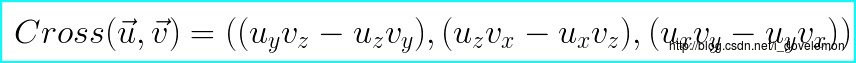
叉积的几何意义上面已经说过了,在左手坐标系中,可以通过左手判定法则,来判断,最后垂直于这两个向量的向量的方向,若在右手坐标系中,就用右手判定法则来进行。
坐标变换
(注:下面用粗体的字表示向量,因为网页不支持向量的书写)
在讲坐标变换之前,我们先来看看这样的情形。
我们都知道,在常温下,水的沸点为100摄氏度。当我们用华氏温度表示的时候,它是212度。也就是说,虽然对于同样的水的沸点,在不同的参考系中,它的描述是不同的。
对向量进行坐标变换
所以,同样的情况,可以出现在向量中。如果我们选择的坐标系不同,那么对同一个向量,它可能有不同的表述方式,如下图中的向量:
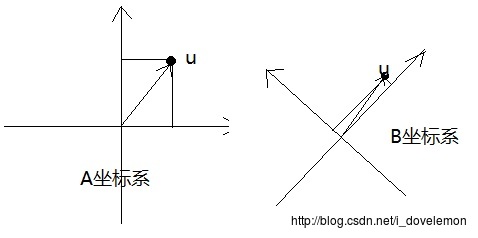
在A坐标系中的向量u,与在B坐标系中的向量是同一个向量,但是,在不同的坐标系中,他们的表示方式不同。
如在A中Ua = (1,1)而在B中为Ub = (2, 0.5)
所以,针对这样的情况,我们需要知道,如何将在A坐标系中表述的坐标,变换为以B坐标系表示的坐标。
现在,我们假设,用U = (Ux, Uy), V = (Vx, Vy)来表示A坐标系的X轴和Y轴在B坐标系中的坐标。那么在上图中的向量,我们现在称之为W,它在B坐标系中的表示方法就是:
Wb = 1 * U + 1 * V
好了,有了这个例子之后,我们来推导一般的情况。
我们假设Wa = (x,y),也就是W向量在A坐标系中的表示方法,U,和V为A坐标系中的X轴单位向量,和Y轴单位向量,在B坐标系中的表示,那么W向量在B坐标系中的表示就可以通过下面的公式推导出来:
Wb = x * U + y * V
所以,只要知道了在A坐标系中的向量坐标W,还有A坐标系的X轴单位向量和Y轴单位向量在B坐标系中的表示,我们就可以通过上面的公式推导出,向量W在B坐标系下的表示了。
对点进行坐标变换
在3D空间中,我们也可以使用一个向量来表示3D空间中的点,这个向量就被称为点向量。对点向量进行坐标变换时,并不能使用上面介绍的对向量进行变换的方法。因为在上面进行向量变换时,我们仅仅考虑了向量的方向,但是对于点向量来说,方向对它没有什么用处,它只关心它的位置。所以我们需要在上面的基础上对点向量做一些处理。
我们在上面对向量进行坐标变换时,由于向量没有位置性,所以没有考虑两个不同的坐标系的位置关系。现在对点向量来说,位置很重要,所以需要考虑一下这两个坐标系之间的位置关系。我们假设在上图中的A坐标系的原点用B坐标系中的坐标表示为O(Ox, Oy),那么只要对上面推导的坐标做一下平移就可以推导出点坐标变换公式了,如下所示:
Wb = x * U + y * V + O
读者可能会问,为什么要进行坐标变化了?为什么不在一个坐标里面进行处理了?
这是因为,有时候,我们在某一个坐标系里面,对问题进行处理,可能会很麻烦,而在另一个坐标系里进行处理,会很容易。所以我们可以将坐标变换到新的坐标系中去解决,然后将结果在变会原来的坐标系里面,这样就会简化很多的工作。熟悉3D流水线的人就会知道,整个3D流水线,都是在进行坐标变化,比如模型坐标到世界坐标变化,世界坐标到相机坐标变化,相机坐标到裁剪体坐标变化,然后到透视坐标,最后到屏幕坐标。这些都是在进行坐标变化。所以,掌握坐标变换,对以后的工作,将会有很大的帮助。
总结
好了,今天的向量就讲到这里。如果读者发现博客中的问题或者有什么地方不是很清楚,可以在留言中进行留言。
以上是关于DirectX 9.0读书笔记 向量的主要内容,如果未能解决你的问题,请参考以下文章