《大话数据结构》学习笔记

Posted 2022-04-26 小公子”

文章目录

• • 第二章 - 算法
  • 第三章 - 线性表
  • • 3.1 单链表
    • • 3.1.1 相关概念
      • 3.1.2 读取
      • 3.1.3 插入
      • 3.1.4 删除
      • 3.1.5 整表创建
      • 3.1.6 整表删除
    • 3.2 静态链表
    • • 3.2.1 相关概念
      • 3.2.2 插入
      • 3.2.3 删除
      • 3.2.4 优缺点
    • 3.3 循环链表
    • • 3.3.1 相关概念
      • 3.3.2 双表合并
    • 3.4 双向链表
    • • 3.4.1 相关概念
      • 3.4.2 插入
      • 3.4.3 删除
  • 第四章 栈与队列
  • • 4.1
    • 4.2
    • 4.3

程序=数据结构+算法

阅读说明：

1. 本文是 《大话数据结构》这本书的阅读笔记，也就是说我写的这些，书中都有，想要看更详细的，可以下载原书看。原书的百度网盘：密码：u942；
2. 只记录原理和思维，不涉及编码实现。想要找代码实现的小伙伴们，这篇文章里面没有哦；
3. 如有不正确的地方，欢迎指正。

（大家一起进步丫）

---

---

第二章 - 算法

1.什么是算法？

Ans：算法是 解决特定问题 求解步骤 的描述。

2.算法的复杂度分为哪两种？

Ans：时间复杂度 和 空间复杂度。一般而言，提算法复杂度，是指算法的时间复杂度。

3.常用的时间复杂度所耗费的时间从小到大依次为？

Ans：$O(1)<O(lo{g}_n)<O(n)<O(nlo{g}_n)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)$

第三章 - 线性表

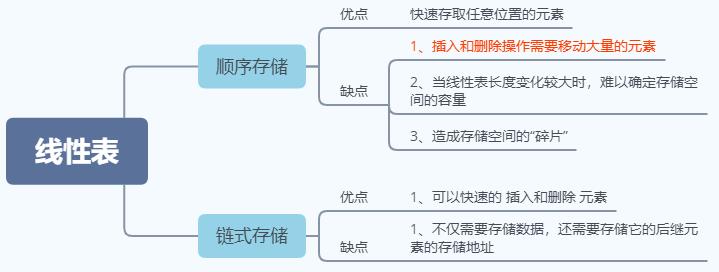
1.线性表的存储方式？以及各存储方式各自的优缺点。

Ans：存储方式有两种：顺序存储和链式存储。

2.单链表相关问题

3.1 单链表

3.1.1 相关概念

• 数据域：存储数据元素信息的域
• 指针域：存储直接后继位置的域
• 指针（链）：指针域中存储的信息
• 结点（存储映像）：数据域+指针域
  
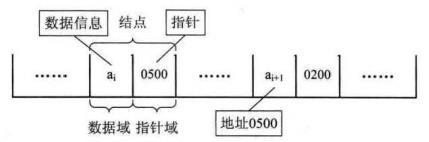
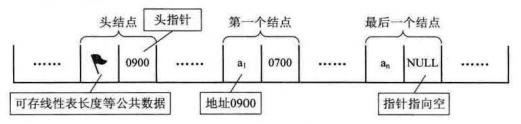
• 头指针：链表中第一个结点的存储位置

• 头结点：在单链表的第一个节点前附设一个结点

  头结点的数据域可以不存储任何信息。也可以存储如线性表的长度等附加信息。
  

3.1.2 读取

核心思想：工作指针后移。（事先不知道要循环多少次【没有定义表长】，所以不可以用for循环）
简单来讲：从头开始找，直到找到第 i 个元素为止。该算法的时间复杂度取决于 i 的位置。最坏情况的时间复杂度为 O(n)。

3.1.3 插入

Question：假设存储元素 e 的结点为 s ，要实现结点p、p->next 和 s 之间逻辑关系的变化，只需要将结点 s 插入到结点 p 和 p->next 之间即可。如何插入呢？

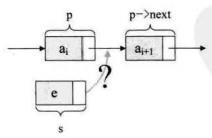
Ans：只需要让 s->next 和 p->next 的指针做一点改变即可。

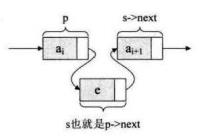
特殊情况，对于单链表的表头和表尾的数据插入，操作是相同的！

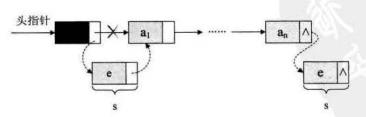
总结

3.1.4 删除

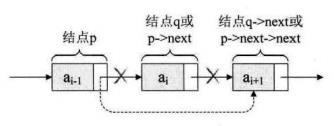
变换指针即可！！！

对于插入和删除 操作越频繁的线性链表，采用链式存储越方便！！！

---

3.1.5 整表创建

• 顺序存储结构的创建，其实就是一个数组的初始化，即声明一个类型和大小的数组并赋值的过程。

• 链表存储结构不像顺序存储结构那么集中，是一种动态结构。

• 对于每个链表来说，它所占用空间的大小和位置是不需要预先分配划定的，可以根据系统的情况和实际的需求即时生成。

头插法：
简要理解：最新的元素在链表的最“前”面！！！（但是，传统思维是 最新的元素要在链表的末尾！）
示意图见下：

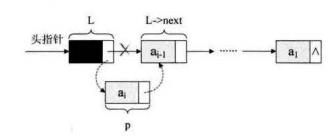
尾插法：
即：最新的元素在链表的末尾！！！（待补充！！！）

---

3.1.6 整表删除

3.2 静态链表

3.2.1 相关概念

• 用数组代替指针来描述单链表
• 数组由两个数据域组成，data 和 cur ，数据域data，用来存放数据，游标 cur 相当于单链表中的 next 指针，存放该元素的后继在数组中的下标。
• 也可称 游标实现法

图片解释：

• 对数组第一个和最后一个元素作特殊处理，不存储数据。
• 第一个元素：即下标为 0 的元素的 cur 中存放备用链表的第一个结点的下标
• 数组的最后一个元素：该cur中存放第一个有数值的元素的下标，相当于单链表中的头节点的作用。
• 备用链表：未被使用的数组元素

举个例子：

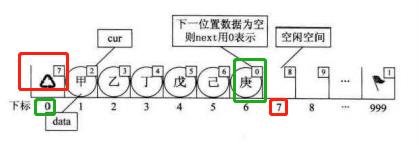
• 其中：Δ 作为下标为 0 的元素，其cur中存放备用链表（空）的第一个结点的下标，即为7（如图所示）；
• 数组的最后一个元素 庚 ，该cur中存放第一个有数值的元素的下标，即为 0（如图所示）.

3.2.2 插入

核心：每当进行插入时，从备用链表上取得第一个结点作为待插入的新结点。

Q：如图，想要将 丙 插入到 乙 和 丁 之间，如何操作？
Ans：

1. 首先将 丙 放在下标为 7 的位置，即备用链表第一位；
2. 更新 乙 的 cur 为 7 ；
3. 更新 丙 的cur 为 3，即 丁 所在的位置。

插入成功！！！示意图如下！

3.2.3 删除

核心：使得删除的位置成为第一个优先空位，把它存入第一个元素的cur中。

了解了静态链表的插入，静态链表的删除也就方便理解了。

Q：链表如上图所示，此时，删除 甲 ？如何操作？

Ans：

1. 首先更新下标为 0 的元素的 cur，更新为 甲 的下标；
2. 更新 已删除元素甲 的 cur 为 备用链表 的第一个元素的 下标，本图中为8.

删除成功，示意图如下。

3.2.4 优缺点

---

3.3 循环链表

---

3.3.1 相关概念

• 解决的问题：如何从当中一个结点（任意一个几点）出发，访问到链表的全部结点。
• 空循环链表 示意图
  
• 非空循环链表 示意图
  

---

3.3.2 双表合并

Q：合并如图所示 两个 循环链表，如何操作？

Ans：

---

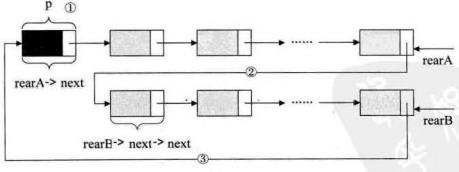
3.4 双向链表

3.4.1 相关概念

• 定义：双向链表就是在单链表的每个结点中，再设置一个指向其前驱节点的指针域。
• 双向链表中的结点都具有两个指针域，一个指向直接后继，另一个指向直接前驱
• 双向链表的循环带头结点 的 空链表 示意图
  
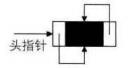
• 非空循环 双向链表 示意图
  

---

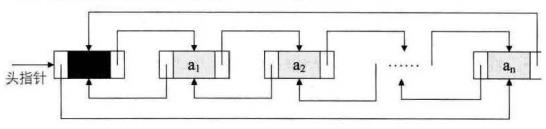
3.4.2 插入

Q：假设存储 s 的结点为 s ，要实现将结点 s 插入到结点p 和 p->next 之间，如何操作？

Ans：

s - >prior = p ; /*把 p 赋值给 s 的前驱*/
s - >next =p - >next; /*把 p->next复制给s的后继*/
p - >next ->prior = s; /*把 s 赋值给p->next的前驱*/
P - >next = s;/*把 s 赋值给 p 的后继*/

注意顺序：
先搞定 s 的前驱和后继，再搞定后结点的前驱，最后搞定前结点的后继！

3.4.3 删除

Q：删除P结点，如何操作？

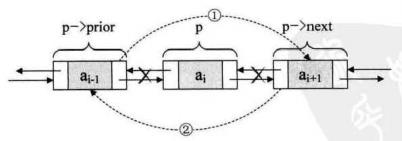
Ans:两步

p->prior->next=p->next;/*把p->next赋值给p->prior 的后继*/
p->next->prior=p->prior;/*把p->prior赋值给p->next的前驱*/

第四章 栈与队列

4.1

4.2

4.3